캐글 메달리스트가 알려주는 캐글 노하우
이 책 읽으면서 공부한 내용 정리함
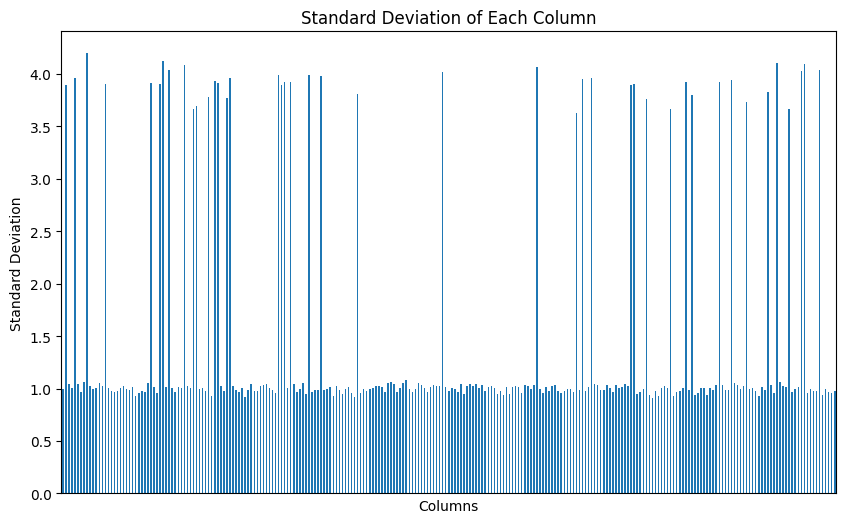
turtle = train.loc[train['wheezy-copper-turtle-magic'] == 123, train.columns.difference(['id', 'target', 'wheezy-copper-turtle-magic'])]
# 'target' 컬럼을 제외한 표준편차 계산
turtle_std = turtle.std()
plt.figure(figsize=(10, 6))
turtle_std.plot(kind='bar')
plt.title('Standard Deviation of Each Column')
plt.xticks([])
plt.xlabel('Columns')
plt.ylabel('Standard Deviation')
plt.show()매직거북이(wheezy-copper-turtle-magic)는 범주형 변수일 확률이 높음
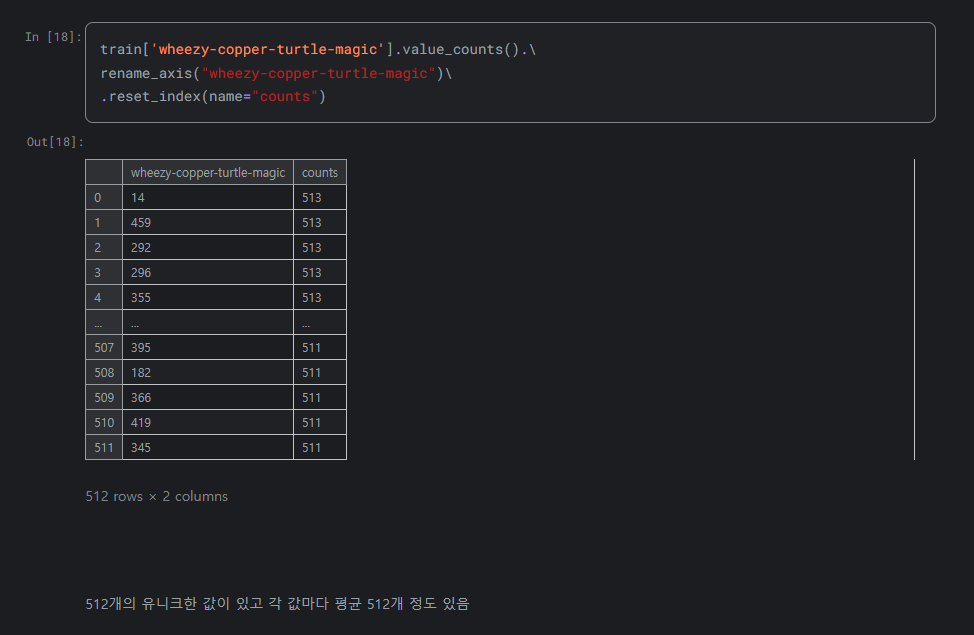
각 범주(매직거북이)로 데이터프레임를 나눔
나눠진 데이터프레임을 터틀이라고 부르겠음
터틀의 컬럼들의 표준편차를 구해서 그래프로 출력하면 전부 썸네일과 비슷한 구조로 나옴
표준편차 1 언저리 컬럼들, 3~4 언저리 컬럼들로 나눠짐
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_val_score
import numpy as np
# 1. 전체 컬럼의 예측력
X_all = turtle
y_all = train.loc[train['wheezy-copper-turtle-magic'] == 123, 'target']
model_all = LogisticRegression(max_iter=1000, random_state=42)
score_all = np.mean(cross_val_score(model_all, X_all, y_all, cv=5))
# 2. 표준편차가 2보다 큰 컬럼의 예측력
high_std_cols = turtle_std[turtle_std > 2].index
X_high_std = turtle[high_std_cols]
model_high_std = LogisticRegression(max_iter=1000, random_state=42)
score_high_std = np.mean(cross_val_score(model_high_std, X_high_std, y_all, cv=5))
# 3. 표준편차가 2보다 작은 컬럼의 예측력
low_std_cols = turtle_std[turtle_std <= 2].index
X_low_std = turtle[low_std_cols]
model_low_std = LogisticRegression(max_iter=1000, random_state=42)
score_low_std = np.mean(cross_val_score(model_low_std, X_low_std, y_all, cv=5))
# 결과 출력
print(f"전체 컬럼의 예측력 (CV 평균 점수): {score_all:.4f}")
print(f"표준편차 > 2 컬럼의 예측력 (CV 평균 점수): {score_high_std:.4f}")
print(f"표준편차 <= 2 컬럼의 예측력 (CV 평균 점수): {score_low_std:.4f}")GPT한테 코드 짜라고 시킴
전체 컬럼의 예측력 (CV 평균 점수): 0.6250
표준편차 > 2 컬럼의 예측력 (CV 평균 점수): 0.6876
표준편차 <= 2 컬럼의 예측력 (CV 평균 점수): 0.5174GPT 말씀
코드를 보니 k-겹 교차 검증(k-Fold Cross-Validation)을 사용하고 있습니다. cross_val_score 함수에서 cv=5로 지정하여 5-겹 교차 검증을 수행하고 있네요. 이 방법은 데이터셋을 5개의 폴드로 나누고, 각 폴드가 한 번씩 테스트 세트가 되어 총 5번 모델을 학습 및 평가하는 방식입니다. 이를 통해 모델의 일반화 성능을 더 정확하게 평가할 수 있습니다.
범주마다 표준편차 2 넘는 컬럼들이 의미가 있을지도?
표준편차 2 넘는 컬럼들은 각 범주마다 다름.
그래서 책에서는 512개의 모델을 각각 만드는 방법을 이야기하는 거 같던데 이거 맞나?
GPT 말씀2 : 피처 표준편차로 찾기랑 후진선택법으로 찾기랑 비교해보고 싶어서 물어봄
표준편차를 기반으로 피처를 선택하는 방법과 후진선택법(Backward Elimination)을 비교해 보겠습니다.
표준편차를 기반으로 한 피처 선택:
- 방법: 각 컬럼의 표준편차를 계산하여 표준편차가 일정 값 이상인 컬럼을 선택합니다.
- 장점:
- 계산이 간단하고 빠릅니다.
- 피처의 변동성을 기준으로 중요한 피처를 선택할 수 있습니다.
- 단점:
- 표준편차가 크다고 해서 반드시 예측 성능에 긍정적인 영향을 미치는 것은 아닙니다.
- 피처 간의 상호작용을 고려하지 않습니다.
후진선택법(Backward Elimination):
- 방법: 모든 피처를 포함한 모델을 시작으로, 가장 기여도가 낮은 피처를 하나씩 제거해 나갑니다. 일반적으로 p-값을 기준으로 합니다.
- 장점:
- 통계적으로 덜 중요한 피처를 제거하여 모델의 단순성을 높입니다.
- 피처 간의 상호작용을 고려할 수 있습니다.
- 단점:
- 계산 비용이 높습니다. 특히 피처 수가 많을 때 시간이 오래 걸릴 수 있습니다.
- p-값 기준이므로, 통계적 유의성을 지나치게 강조할 수 있습니다.
두 방법 모두 피처 선택에 유용하지만, 데이터의 특성과 목적에 따라 적절한 방법을 선택하는 것이 중요합니다. 표준편차 기반 방법은 간단하고 빠르지만, 후진선택법은 더 정교하고 통계적으로 신뢰할 수 있는 결과를 제공할 수 있습니다.
p-값은 통계적 가설 검정에서 사용되는 중요한 개념으로, 관찰된 데이터가 귀무가설(null hypothesis)이 참일 때 나타날 확률을 나타냅니다. 좀 더 구체적으로 설명하자면:
-
가설 설정:
- 귀무가설 (H0): 검증하려는 기본 가정. 예를 들어, "이 피처는 모델 성능에 유의미한 영향을 미치지 않는다."
- 대립가설 (H1): 귀무가설의 반대 가정. 예를 들어, "이 피처는 모델 성능에 유의미한 영향을 미친다."
-
검정 통계량 계산:
- 데이터에서 검정 통계량을 계산합니다. 이 통계량은 데이터를 요약한 값입니다.
-
p-값 계산:
- 검정 통계량의 분포를 바탕으로 p-값을 계산합니다. 이는 귀무가설이 참일 때 검정 통계량이 관찰된 값보다 더 극단적인 값을 가질 확률입니다.
-
결정 기준:
- 미리 정해진 유의 수준(α, 보통 0.05)과 비교하여 p-값을 해석합니다.
- p-값 < α: 귀무가설을 기각하고 대립가설을 채택합니다. 즉, 피처가 모델 성능에 유의미한 영향을 미친다고 결론짓습니다.
- p-값 ≥ α: 귀무가설을 기각하지 않습니다. 즉, 피처가 모델 성능에 유의미한 영향을 미친다고 결론짓지 않습니다.
예시:
피처 선택 과정에서 p-값이 0.03이라면, 이는 귀무가설이 참일 때 이러한 결과가 발생할 확률이 3%라는 의미입니다. 보통 유의 수준을 0.05로 설정하므로, p-값이 0.05보다 작으므로 귀무가설을 기각하고 피처가 유의미하다고 결론 내립니다.
이 과정을 통해 통계적으로 유의미한 피처를 식별하고, 모델에 포함시킬 피처를 결정할 수 있습니다.
😊
