해시 함수 (Hash Function)

해시 함수는 데이터를 고정된 길이의 해시값으로 변환하는 함수이다. 해시 함수를 이용한 저장, 삭제, 검색은 모두 $O(1)$의 시간 복잡도를 가진다. 대표적인 해시 함수로 나머지를 사용하는 방법이 있다.

---

Direct Access Table

Direct Access Table은 key 값이 k인 데이터를, 배열의 index k에 저장하는 방식이다.

• 장점
  Direct Access Table은 키를 인덱스로 사용하여, 값을 검색할 시 O(1)의 시간 복잡도로 매우 빠르게 접근할 수 있게 한다. 즉, 어떤 크기의 데이터셋이든 검색 시간은 일정하다는 장점이 있다.

• 단점
  key의 범위가 크거나 키 값이 연속적이지 않은 경우, 많은 메모리 공간이 사용되지 않은 채 낭비될 수 있다.

Direct Access Table의 단점을 해결하기 위해, 해시 함수를 이용하는 해시 테이블이 주로 사용된다.

---

해시 테이블 (Hash Table)

해시 테이블은 Direct Access Table의 개념을 확장하면서도 그 단점을 극복하기 위해 개발된 자료구조이다. 해시 테이블은 키(key)에 해시 함수를 적용하여 데이터를 저장하고 검색하는 방식을 사용한다. 이 방식은 데이터의 저장, 삭제, 검색 모두에서 평균적으로 $O(1)$의 시간 복잡도를 가진다. 해시 함수는 아래의 요소들로 구성된다.

• 해시 함수 (Hash Function): 키를 배열의 인덱스로 변환하는 함수이다. 해시 함수는 고르게 해시값을 분포하여 충돌의 가능성을 줄이는 것이 중요하다.

• 버킷 (Bucket): 해시 테이블의 각 셀을 버킷이라고 하며, 하나의 버킷에 하나 이상의 키-값 쌍을 저장할 수 있다.

• 충돌 처리 방법 (Collision Resolution Technique): 두 개의 키가 동일한 해시값을 가질 때 발생하는 충돌을 처리하는 방법이다.

해시 테이블의 충돌 처리 방법은 크게 Chaining과 Open Addressing두 가지가 있다.

---

1. Chaining

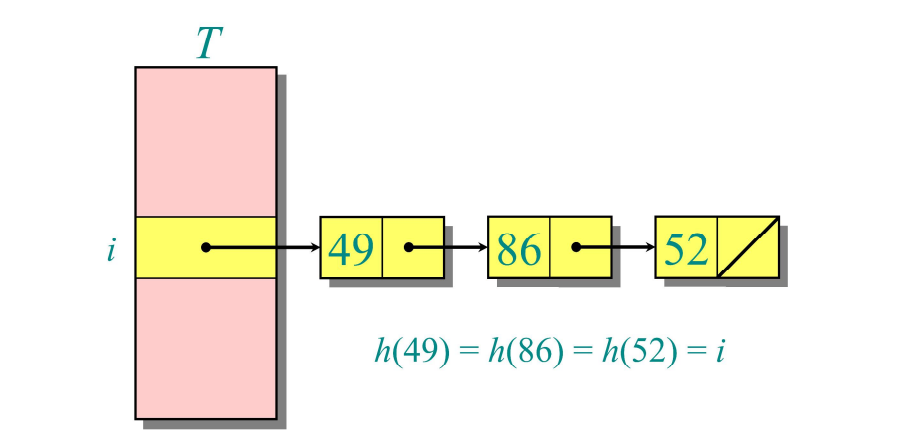
Chaining은 해시 테이블에서 충돌을 해결하는 한 방법으로, 동일한 해시 값을 가지는 여러 키를 연결 리스트로 관리하는 방식이다. 위의 그림과 같이, 해시 함수 h를 49, 86, 52에 적용한 결과가 모두 i로 같을 경우, 해당 버킷의 연결 리스트에 새로운 노드를 추가하는 방식으로 데이터를 저장한다.

Example)
해시 함수 $h(k) = k\ mod\ m$일 때 (k를 m으로 나눈 나머지), Chaining 기법을 사용하여 길이가 3인 해시 테이블에 12, 11, 17, 5, 19, 27, 4, 2, 13을 순차적으로 삽입하는 예시.

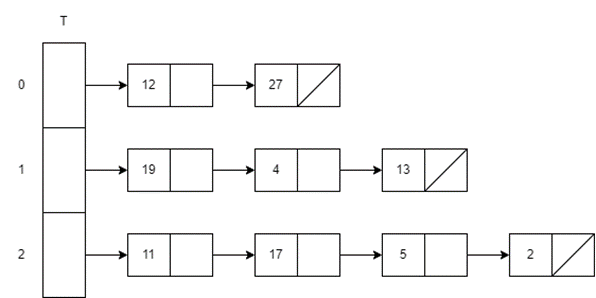
• 12 삽입
  $h(12)=12\ mod\ 3=0$
  Index 0
• 11 삽입
  $h(11)=11\ mod\ 3=2$
  Index 2
• 17 삽입
  $h(17)=17\ mod\ 3=2$
  Index 2, link after 11
• 5 삽입
  $h(5)=5\ mod\ 3=2$
  Index 2, link after 17
• 19 삽입
  $h(19)=19\ mod\ 3=1$
  Index 1
• 27 삽입
  $h(27)=27\ mod\ 3=0$
  Index 0, link after 12
• 4 삽입
  $h(4)=4\ mod\ 3=1$
  Index 1, link after 19
• 2 삽입
  $h(2)=2\ mod\ 3=2$
  Index 2, link after 5
• 13 삽입
  $h(13)=13\ mod\ 3=1$
  Index 1, link after 4

---

2. Open Addressing

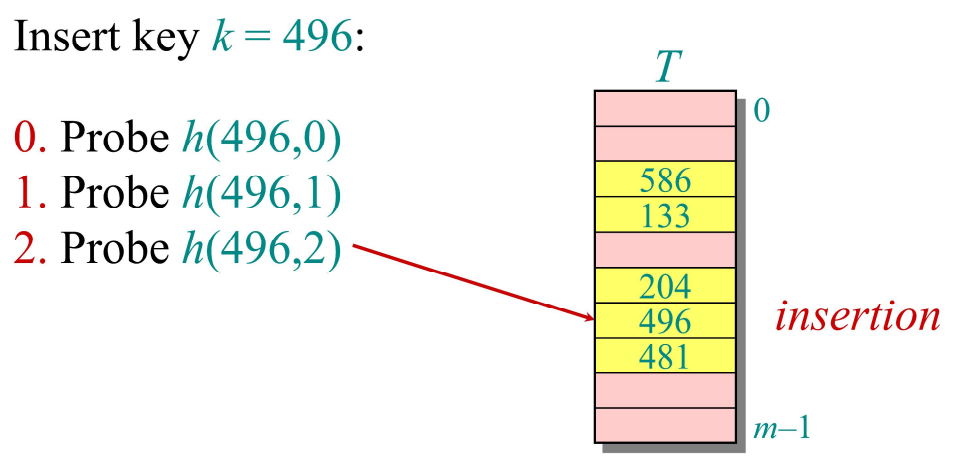
Open Addressing은 해시 테이블에서 충돌을 해결하는 또 다른 방법으로, 별도의 공간이나 연결 리스트를 사용하지 않고, 해시 테이블의 빈 버킷에 데이터를 저장하는 방식이다. Open Addressing은 충돌이 발생할 경우 탐사(Probing)과정을 통해 다른 빈 버킷을 찾는다. 위의 그림에서 볼 수 있듯이, 496이라는 key를 저장하기 위해 먼저 h(496, 0)을 수행한다. (여기서 0은 probing number로, 첫 번째 시도의 경우 해당 파라미터는 0이 된다.) 해당 위치에서 collision이 발생하면 probing number를 1씩 증가시키며 빈 버킷을 찾을 때까지 탐사를 반복한다. 위의 예시에서는 h(496, 2) 결과 빈 버킷에 도달한 것을 볼 수 있다.

탐사 기법은 아래의 세 가지가 있다.

• 선형 탐사 (Linear Probing)
  충돌이 발생하면, 한 칸씩 순차적으로 이동하며 다음 비어 있는 버킷을 찾는다.

• 이차 탐사 (Quadratic Probing)
  충돌이 발생하면, 이차 함수($1^2, 2^2, 3^2...$ 등)를 사용하여 다음 버킷 위치를 계산한다.

• 이중 해싱 (Double Hashing)
  두 번째 해시 함수를 사용하여 다음 버킷 위치를 계산한다. 이 방법은 탐사 패턴을 더 다양하게 하여 클러스터링 문제를 줄일 수 있다. 클러스터링 문제는 해시 테이블에서 특정 부분에 데이터가 집중적으로 모이는 현상을 말한다.

선형 탐사와 같이 단순한 방법은 클러스터링 문제에 취약한데, 같은 부분에서 충돌이 일어날 때마다 점점 탐사 시간이 길어지기 때문이다.

Example)
해시 함수 $h'(k) = k\ mod\ m$일 때, Open Addressing 기법을 사용하여 길이가 11인 해시 테이블에 18, 9, 27, 16, 5, 21, 6, 7을 순차적으로 삽입하는 예시.

1. Linear Probing
$h(k,i)=(h'(k)+i)\ mod\ m$

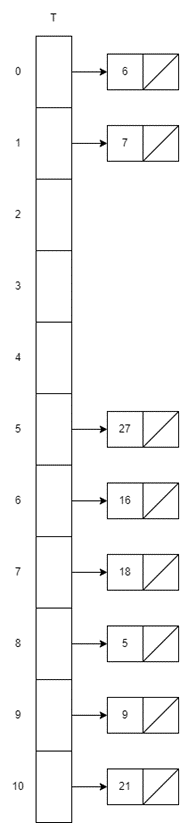
• Insert 18
  $i=0,\ h(18,0)=18\ mod\ 11=7$
  place at index 7
• Insert 9
  $i=0,\ h(9,0)=9\ mod\ 11=9$
  place at index 9
• Insert 27
  $i=0,\ h(27,0)=27\ mod\ 11=5$
  place at index 5
• Insert 16
  $i=0,\ h(16,0)=16\ mod\ 11=5$
  collision at index 5
  $i=1,\ h(16,1)=17\ mod\ 11=6$
  probe to index 6
• Insert 5
  $i=0,\ h(5,0)=5\ mod\ 11=5$
  collision at index 5
  $i=1,\ h(5,1)=6\ mod\ 11=6$
  probe to index 6 (taken)
  $i=2,\ h(5,2)=7\ mod\ 11=7$
  probe to index 7 (taken)
  $i=3,\ h(5,3)=8\ mod\ 11=8$
  probe index 8
• Insert 21
  $i=0,\ h(21,0)=21\ mod\ 11=10$
  place at index 10
• Insert 6
  $i=0,\ h(6,0)=6\ mod\ 11=6$
  collision at index 6
  $i=1,\ h(6,1)=7\ mod\ 11=7$
  probe to index 7 (taken)
  $i=2,\ h(6,2)=8\ mod\ 11=8$
  probe to index 8 (taken)
  $i=3,\ h(6,3)=9\ mod\ 11=9$
  probe to index 9 (taken)
  $i=4,\ h(6,4)=10\ mod\ 11=10$
  probe to index 10 (taken)
  $i=5,\ h(6,5)=11\ mod\ 11=0$
  probe to index 0
• Insert 7
  $i=0,\ h(7,0)=7\ mod\ 11=7$
  collision at index 7
  $i=1,\ h(7,1)=8\ mod\ 11=8$
  probe to index 8 (taken)
  $i=2,\ h(7,2)=9\ mod\ 11=9$
  probe to index 9 (taken)
  $i=3,\ h(7,3)=10\ mod\ 11=10$
  probe to index 10 (taken)
  $i=4,\ h(7,4)=11\ mod\ 11=0$
  probe to index 0 (taken)
  $i=5,\ h(7,5)=12\ mod\ 11=1$
  probe to index 1

2. Quadratic Probing
$h(k,i)= (h'(k)+c_1 i+c_2 i^2 )\ mod\ m\\ (c_1 = 1, c_2 = 2)$

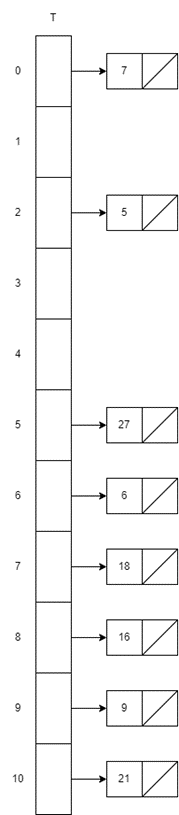
• Insert 18
  • $i=0,\ h(18,0)=18 \mod 11=7$
    Place at index 7
• Insert 9
  • $i=0,\ h(9,0)=9 \mod 11=9$
    Place at index 9
• Insert 27
  • $i=0,\ h(27,0)=27 \mod 11=5$
    Place at index 5
• Insert 16
  • $i=0,\ h(16,0)=16 \mod 11=5$
    Collision at index 5
  • $i=1,\ h(16,1)=(5+1*1+3*1) \mod 11=9 \mod 11=9$
    Collision at index 9
  • $i=2,\ h(16,2)=(5+1*2+3*4) \mod 11=19 \mod 11=8$
    Probe to index 8
• Insert 5
  • $i=0,\ h(5,0)=5 \mod 11=5$
    Collision at index 5
  • $i=1,\ h(5,1)=(5+1*1+3*1) \mod 11=9 \mod 11=9$
    Collision at index 9
  • $i=2,\ h(5,2)=(5+1*2+3*4) \mod 11=19 \mod 11=8$
    Collision at index 8
  • $i=3,\ h(5,3)=(5+1*3+3*9) \mod 11=35 \mod 11=2$
    Probe to index 2
• Insert 21
  • $i=0,\ h(21,0)=21 \mod 11=10$
    Place at index 10
• Insert 6
  • $i=0,\ h(6,0)=6 \mod 11=6$
    Place at index 6
• Insert 7
  • $i=0,\ h(7,0)=7 \mod 11=7$
    Collision at index 7
  • $i=1,\ h(7,1)=(7+1*1+3*1) \mod 11=11 \mod 11=0$
    Place at index 0

3. Double Hashing
$h(k,i)= (h'(k)+ih_2 (k)\ mod\ m\\ h_2 (k)=1+(k\ mod\ (m-1))$

• Insert 18
  • $i=0,\ h(18,0)=18 \mod 11=7$
    Place at index 7
• Insert 9
  • $i=0,\ h(9,0)=9 \mod 11=9$
    Place at index 9
• Insert 27
  • $i=0,\ h(27,0)=27 \mod 11=5$
    Place at index 5
• Insert 16
  • $i=0,\ h(16,0)=16 \mod 11=5$
    Collision at index 5
  • $i=1,\ h(16,1)=(5+1*(1+16 \mod 10)) \mod 11=12 \mod 11=1$
    Probe to index 1
• Insert 5
  • $i=0,\ h(5,0)=5 \mod 11=5$
    Collision at index 5
  • $i=1,\ h(5,1)=(5+1*(1+5 \mod 10)) \mod 11=11 \mod 11=0$
    Probe to index 0
• Insert 21
  • $i=0,\ h(21,0)=21 \mod 11=10$
    Place at index 10
• Insert 6
  • $i=0,\ h(6,0)=6 \mod 11=6$
    Place at index 6
• Insert 7
  • $i=0,\ h(7,0)=7 \mod 11=7$
    Collision at index 7
  • $i=1,\ h(7,1)=(7+1*(1+7 \mod 10)) \mod 11=15 \mod 11=4$
    Place at index 4