서론
벨로그 정리할 글을 찾다가 힙 정렬에 대해서 정리해둔게 없어서 이참에 다시 복습하려고 한다.
Heap 자료구조
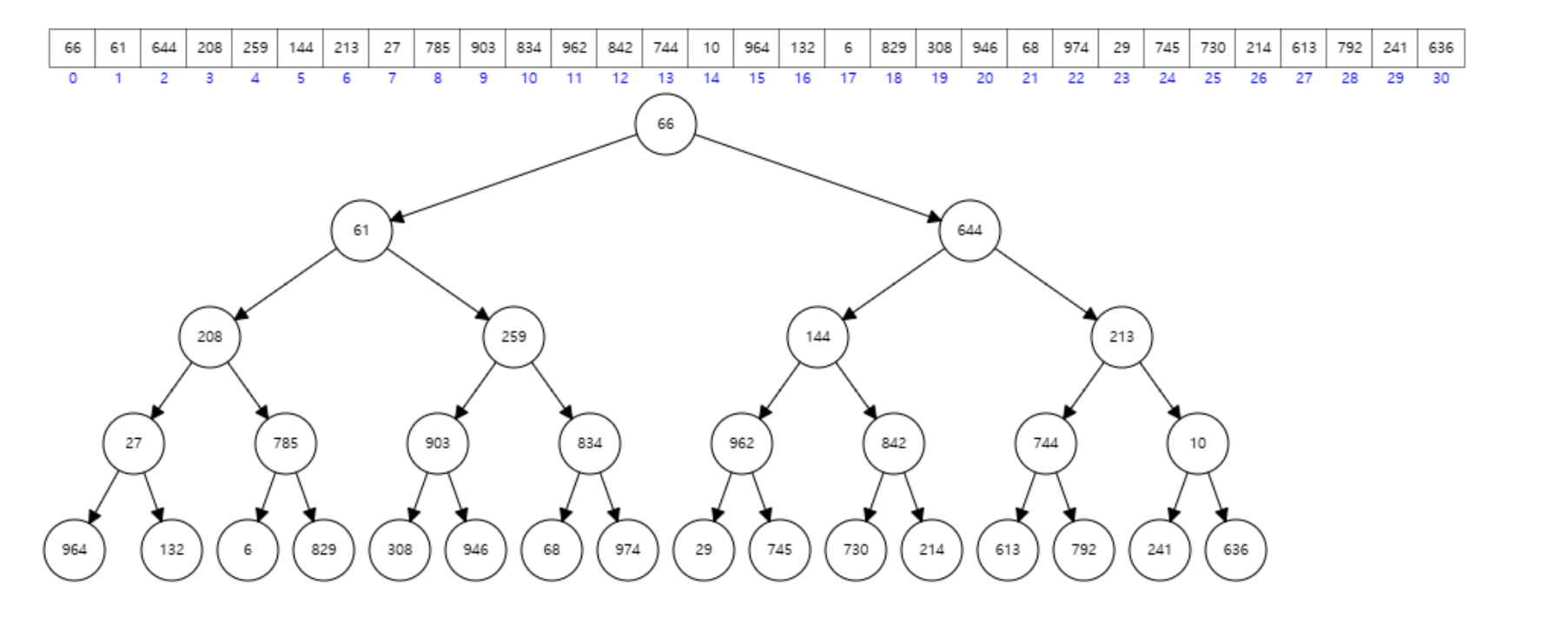
힙은 완전 이진 트리의 한 종류로, 각 노드의 값이 그 자식 노드 값보다 작은지, 큰지에 따라 정렬된 이진 트리다.
일반적으로 배열로 구현되며, 배열의 각 요소가 힙의 노드에 대응된다.
아래 이미지의 트리가 완전 이진 트리로 위에서 아래로, 왼쪽에서 오른쪽으로 순서대로 채워지는 규칙을 가진 트리다.
이진 트리이기 때문에 자식 노드는 당연히 최대 2개 까지 가질 수 있다.
힙은 주로 최솟값 또는 최댓값을 빠르게 찾아내기 위해 사용된다.
Heap의 종류
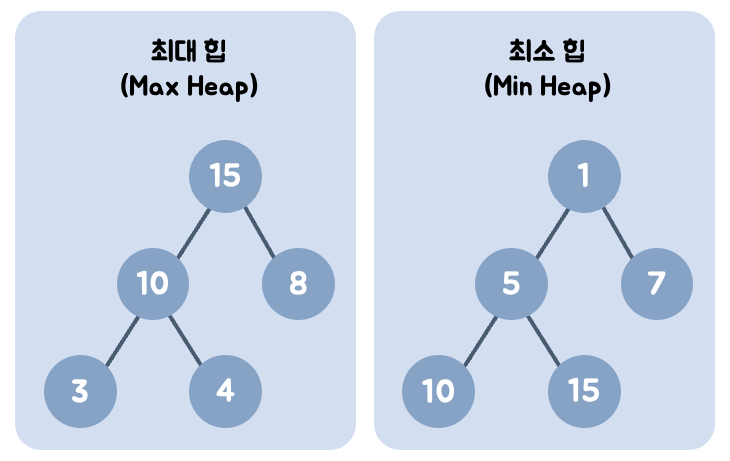
힙의 종류는 크게 두 가지로 최대 힙과 최소 힙이 존재한다.
Max Heap
최대 힙은 모든 노드에 대해 부모 노드의 값이 자식 노드의 값보다 크거나 같다. 즉, 루트 노드가 트리의 최대값이 되기 때문에 최댓값을 빠르게 찾을 수 있다.
최대 힙은 우선순위 큐와 같은 곳에 많이 응용되어 사용된다. 우선순위 큐는 가장 높은 우선순위를 가진 요소가 먼저 나오는 자료구조이며, 최대 힙을 사용하여 구현하면 삽입, 삭제 연산이 O(log n)의 시간 복잡도를 가진다.
Min Heap
최소 힙은 모든 노드에 대해 부모 노드의 값이 자식 노드의 값보다 작거나 같다. 즉, 루트 노드가 트리의 최솟값이 되기 때문에 최솟값을 빠르게 찾을 수 있다.
최소 힙도 최대 힙과 마찬가지로 우선순위 큐와 같은 곳에 응용해서 사용할 수 있다. 마찬가지로 최소 힙을 사용하여 구현하면 삽입, 삭제 연산이 O(log n)의 시간 복잡도를 가진다.
Heap Sort
이제 힙 자료구조와 힙의 특징에 대해서 알아봤으니 초기 힙 구성, 삽입, 삭제 시 발생하는 정렬 알고리즘에 대해서 알아보자.
-
n개의 노드에 대한 완전 이진 트리를 구성한다.
-
최대 힙을 구성한다. 자식 노드가 단말 노드인 부모 노드부터 구성하며, 아래부터 루트까지 올라오면서 순차적으로 만들어 간다.
-
만들어진 최대 힙의 루트 노드를 마지막 노드와 교환하면서 마지막 노드가 된 루트 노드를 제거한다. (제거된 루트 노드는 배열에 추가한다.)
-
최솟값이 된 루트 노드부터 자식 노드와 값을 비교해 교환하며 트리를 재조정한다.
-
3과 4를 반복해서 트리를 재조정하며 배열을 정렬한다.
아래 주소에서 힙 정렬의 과정을 눈으로 쉽게 확인할 수 있다.
Heap Sort Visualization
Heap Sort의 특징
힙 정렬은 일반적으로 다른 정렬 알고리즘에 비해 느린 편에 속하지만, 안정적인 추가 메모리를 요구하지 않고, 항상 일정한 시간 복잡도를 보장하는 특성 때문에 일부 특정한 상황에서 유용하게 사용될 수 있다.
힙 정렬은 추가적인 배열을 필요로 하지 않고, 입력 배열 내에서 정렬을 수행하므로 공간 복잡도가 O(1)이다. 또한 시간 복잡도는 O(n log n)으로, 힙을 구성하는 단계에서 O(n)의 시간이 소요되고, 각 루트 노드를 제거하고 재조정하는 과정이 최악의 경우 O(log n)의 시간이 소요된다.
-
In-place 정렬: 힙 정렬은 추가적인 배열을 필요로하지 않고, 입력 배열 내에서 정렬을 수행하므로 공간 복잡도가 O(1)이다.
-
비교 기반 정렬 알고리즘: 힙 정렬은 비교 기반의 정렬 알고리즘으로, 요소들 간의 비교를 기반으로 정렬한다. 이 때문에 정렬되는 요소들은 반드시 비교 연산이 가능해야 한다.
-
시간 복잡도: 힙 정렬의 시간 복잡도는 O(n log n)이다.
-
비안정적: 힙 정렬은 안정적인 정렬 알고리즘이 아니다. 동일한 키 값을 가진 요소의 상대적인 순서가 정렬 전과 정렬 후에 보장되지 않는다.
마무리
힙 정렬에 대해서 최대한 간략하게 추려서 정리했다. 아마 처음 공부하는 것이 아닌 복습용으로는 나쁘지 않은 것 같다.
아래 사이트에서 여러 복잡한 알고리즘을 쉽게 이해할 수 있다. 힙 정렬은 과정 한두번 보면 바로 다시 생각날 것이다.
