Graph

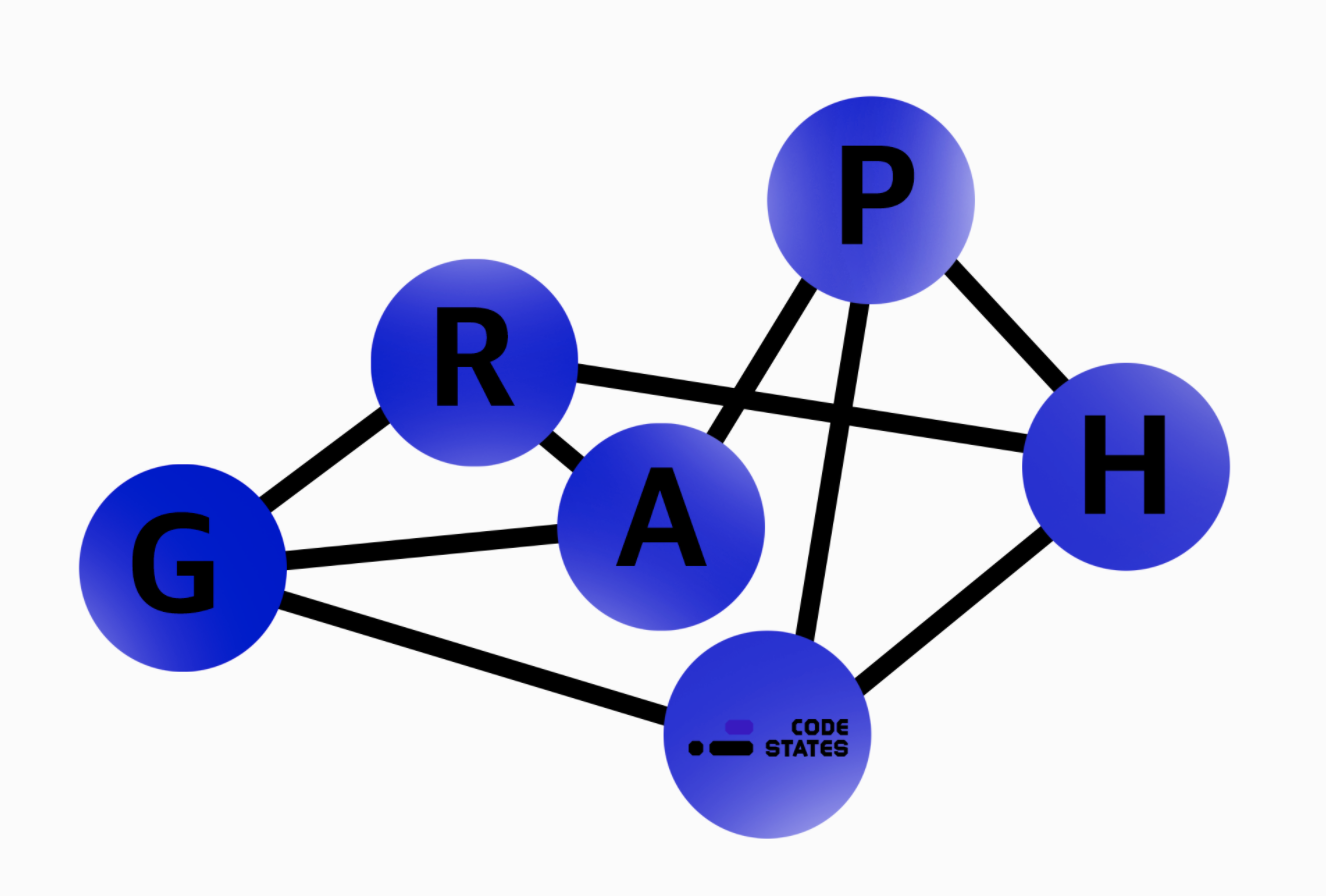
그래프, 위의 그림이 자료구조의 그래프다. 우리가 흔히 아는 그래프랑은 차원이 다르게 생겼다. 보자마자 머리가 아프게 생겼다. 그래프는 '여러개의 점들이 서로 복잡하게 연결되어 있는 관계를 표현한 자료구조'이다. 그래프는 여러개의 정점과 간선으로 구성되어 있다.

정점 : 그래프에 그려진 동그라미 부분, 하나의 대상 그 자체를 나타낸다.
간선 : 정점을 잇는 선들, 대상들이 관계를 가지고 있으면 이어진다.

간선의 표현 방식에 따라서 두가지 그래프로 나뉘어 진다.

• 가중치 그래프 : 간선에 두 정점 사이의 관계를 표시한 그래프
• 비가중치 그래프 : 관계는 표시하지 않고 간선만 이어 놓은 그래프

알아둬야 할 그래프 용어

• 무향그래프 : 방향이 없는 그래프를 말한다. 다시 말해 왕복이 가능한 그래프를 말한다. 반대로 방향그래프는 일방적인 관계를 가진 그래프를 말한다.
• 진입차수(In-degree) : 한 정점에 진입하는(들어오는) 간선의 수
• 진출차수(Out-degree) : 한 정점에서 진출하는(나가는) 간선의 수
• 인접(adjacency) : 두 정점이 간선 하나로 이어진 관계
• 자기 루프(self loop) : 진출한 간선이 바로 자기 자신에게 진입하는 것 (다른 정점 거침 X)
• 사이클(cycle) : 진출한 간선이 다른 정점을 거쳐서 다시 자기 자신에게 돌아오는 것

그래프의 표현 방식 : 인접 행렬, 인접 리스트

인접행렬

인접을 행렬로 나타낸 것, 모든 정점들을 행과 열로 나타내고 관계가 있으면 1을 없으면 0을 표기한다.

A : C와 관계를 가지고 있다.
B : A, C와 관계를 가지고 있다.
C : A와 관계를 가지고 있다.
인접 행렬이 대각선 방향으로 대칭을 이뤘을 때 값이 같다면 그 관계는 양방향을 나타낸다.

인접 행렬을 언제 사용하면 좋을까?

• 단순히 두 정점 사이의 관계를 유무를 파악할 때 용이, 가장 빠른 경로를 찾을 때 주로 사용

인접 리스트

각 정점의 관계를 리스트로 나타낸 것, 각 정점마다 하나의 리스트를 가지고 있고 그 리스트에는 인접한 다른 정점들이 담겨 있다.

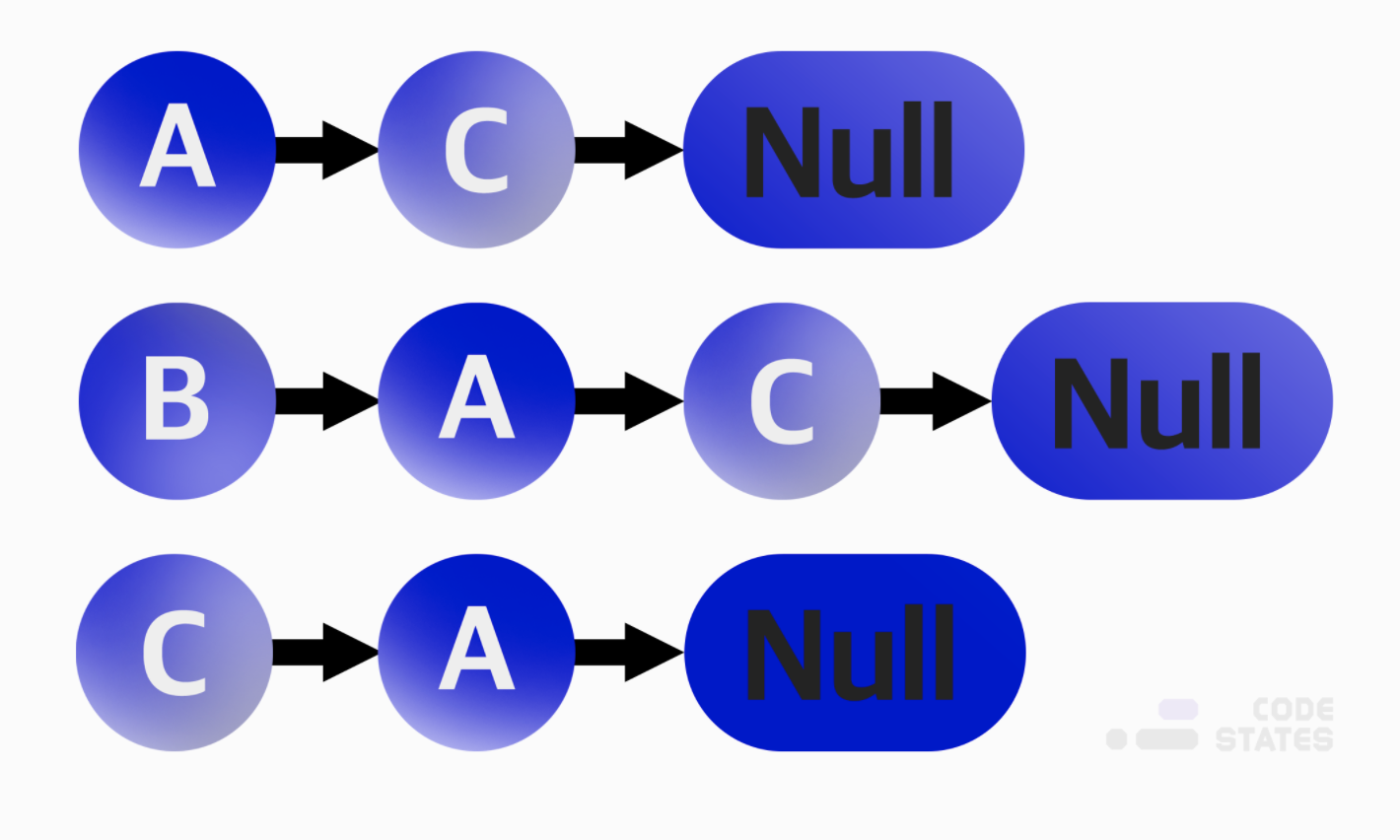
위 인접행렬을 리스트로 나타낸 것이다.
인접 리스트는 언제 사용하면 좋을까?

• 인접행렬은 모든 경우의 수를 저장하기 때문에 메모리를 많이 차지한다. 메모리를 효율적으로 사용할 때 인접 리스트를 사용한다.

Tree

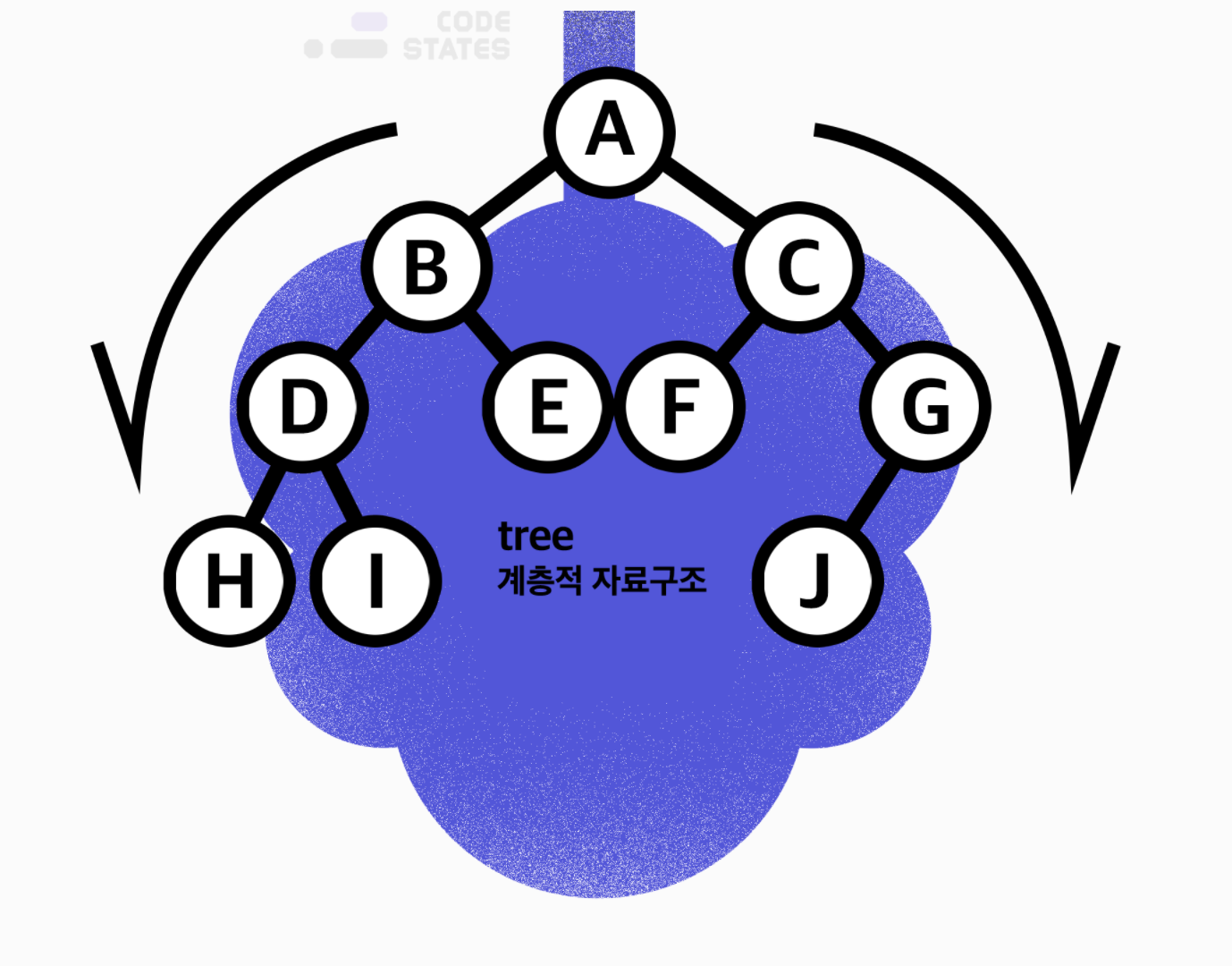
트리 구조는 사진과 같이 나무를 거꾸로 뒤집어 둔 것 같은 모양을 하기 때문에 트리 구조라 부른다. 트리구조는 하나 이상의 데이터가 단방향으로 연결되는 계층적 구조이다. 선형의 구조가 아닌 비선형 구조를 가지고 있다.

알아둬야 할 트리 용어

• 루트 : 트리의 최상위 노드
• 노드 : 트리에서 표현된 하나의 원
• 부모 노드 : 특정 노드의 상위 노드
• 자식 노드 : 특정 노드의 하위 노드
• 형제 노드 : 부모 노드가 같은 노드
• 리프 노드 : 하위 노드가 없는 노드

BST

BST(Binary Search Tree : 이진 탐색 트리)는 트리 구조에서 효율적인 탐색을 위해 사용합니다.

이진트리 : 자식 노드가 최대 두 개인 노드들로 구성된 트리

이진 탐색 트리의 값은 '왼쪽 노드 < 부모 노드 < 오른쪽 노드'의 특징을 가지고 있어야 한다.

여기서 탐색 방법은 3가지의 순회 방식을 가지고 각 순회 방식의 특징은 다음과 같다.

• 전위 순회(Preorder) : '부모 노드 -> 왼쪽 노드 -> 오른쪽 노드' 순서로 조회
• 중위 순회(Inorder) : '왼쪽 노드 -> 부모 노드 -> 오른쪽 노드' 순서로 조회
• 후위 순회(Postorder) : '왼쪽 노드 -> 오른쪽 노드 -> 부모 노드' 순서로 조회

다음과 같은 순회 방식을 취하고 있다. 부모 노드를 언제 조회 하느냐에 따라 명칭을 기억하고 이해한다면 한결 수월해진다.