🔗 링크
https://programmers.co.kr/learn/courses/30/lessons/62048
🔳 문제
가로길이 W, 세로 길이가 H인 직사각형에서 대각선 꼭지점 2개를 잇는 방향으로 선을 그었을 때,
선이 그어지지 않은 정사각형의 갯수를 구해야한다.
👀 예제로 문제 파악하기
입력 : w 8, h 12
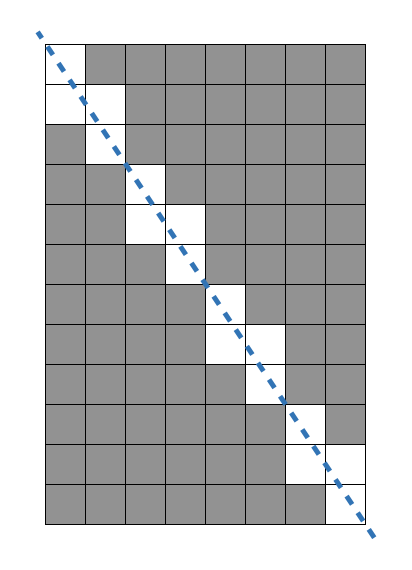
가로가 8, 세로가 12인 직사각형이 있고, 각 대각선 꼭지점에서 선을 그으면
위 사진처럼 잘리게 된다.
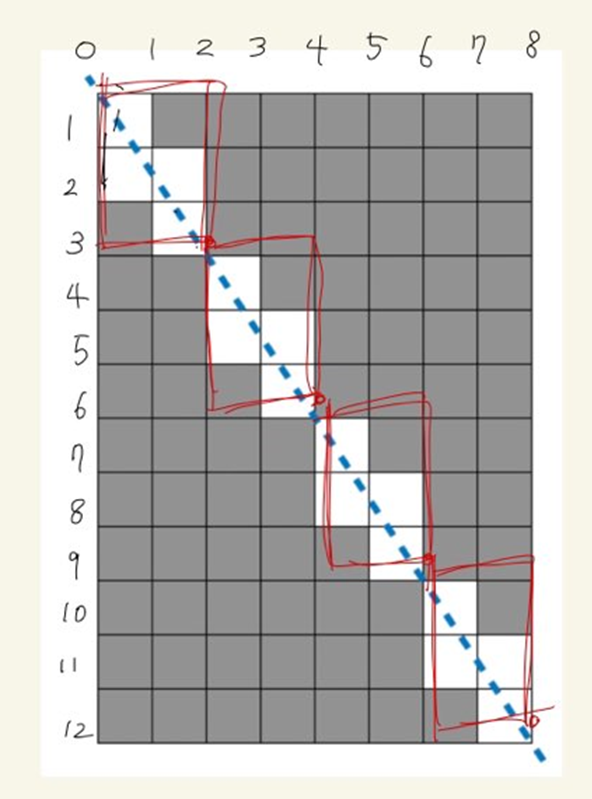
그리고 빨간색 펜으로 쳐져있는 것 처럼 반복되는 것을 확인할 수 있다.
이때 반복이 끝나는 지점의 좌표를 구하면 아래와 같이 나오게 된다.
[2, 3] / [4, 6] / [6, 9] / [8, 12]
x(총 길이 : 8)는 2씩, y(총 길이 : 12)는 3씩 증가하는 패턴을 찾을 수 있는데,
8 → 2
12 → 3으로 되는 조건을 찾아보니, 둘 다 4로 나눈 값인 것을 발견할 수 있었다.
그리고 4는 8과 12의 최대 공약수였다.
따라서 패턴 직사각형의 크기는 2(w/최대공약수)*3(h/최대공약수)가 된다.
그리고 패턴 직사각형에서 사용하지 못하는 정사각형을 빼야하는데,
이때 사용하지 못하는 정사각형을 구하기 위해서는
총 정사각형 갯수 - (가로 길이 + 세로길이 - 1)이 된다.
이 공식이 나온 이유는 아래와 같다.

패턴 직사각형이 다음 꼭짓점으로 도달하기 위해서는 가로 길이, 세로 길이만큼 움직여야하는데,
가로 길이, 세로 길이 중에 겹치는 부분(파란색 부분) 이 있기 때문에 1을 빼는 것이다.
그러면 한 패턴당 사용하지 못하는 정사각형의 갯수를 구했으니,
이 패턴이 몇 번 반복하는지 알아야하는데, 이 패턴은 최대 공약수(4)만큼 반복했다.
따라서 나온 공식은 이랬다.
(전체 크기) - (한 패턴 직사각형 당 사용하지 못하는 정사각형 크기 * 반복횟수)
(w * h) - (((w / 최대공약수) + (h / 최대공약수) - 1) * 최대공약수)
우연의 일치인가? 싶어서 다른 예제를 만들어보았다.
입력 : w 6, h 9
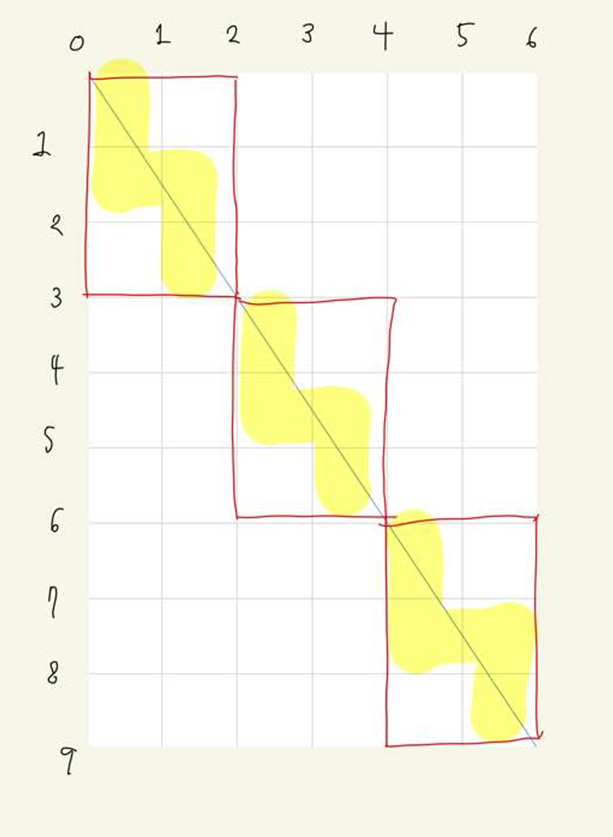
6과 9의 최대 공약수는 3이고,
패턴은 최대공약수만큼 반복했다.
따라서 공식에 그대로 대입해보면
(6 * 9) - ((6 / 3) + (9 / 3) - 1) * 3 = 54 - 12 = 42로, 정답이 제대로 나온다.
😮 알고리즘 풀이 순서
- w와 h의 최대 공약수(gcd)를 구한다.
(w * h) - (((w / gcd) + (h / gcd) - 1) * gcd)를 리턴한다.- 단, w와 h는 각각 1억까지 가능하기 때문에 계산 과정에서 long 타입으로 형변환을 해준다.
- 단, w와 h는 각각 1억까지 가능하기 때문에 계산 과정에서 long 타입으로 형변환을 해준다.
👨💻 코드
public class Solution {
public long solution(int w, int h) {
int gcd = BigInteger.valueOf(w).gcd(BigInteger.valueOf(h)).intValue();
return ((long) w * (long) h) - ((((long) w / gcd) + ((long) h / gcd) - 1) * gcd);
}
@Test
public void 정답() {
Assert.assertEquals(80, solution(8, 12));
Assert.assertEquals(80, solution(12, 8));
Assert.assertEquals(12, solution(4, 4));
}
}

조하요