[백준]2042_구간 합 구하기

https://www.acmicpc.net/problem/2042

Solved

✔ 자료구조 / 세그먼트 트리
✔ 문제 자체의 직관적 해결방법이 너무나도 세그먼트 트리/인덱스 트리의 동작 원리와 같다. 이번 풀이는 세그먼트 트리의 풀이
✔ 세그먼트 트리와 인덱스 트리

• 공통점: 각 구간의 대표값(ex. 합, 최대값 등)을 빠르게 구할 수 있는 자료구조
• 세그먼트 트리: 배열의 크기가 N일 때 임의의 구간에 대한 쿼리를 O(logN)에 수행할 수 있다.
• 인덱스 트리: 세그먼트 트리보다 간단하고 속도가 빠르다. 추가예정 참고

✔ 크기가 N인 배열이 존재할 때
→트리의 높이 = ceil(log2(N))
→트리의 높이가 H일 때, 세그먼트 트리의 크기 = 1 << (H + 1)

✔ 수의 최대 개수는 백만개(1,000,000), 트리의 높이 = log2(백만) = 20, 세그먼트 트리의 크기 1<<21

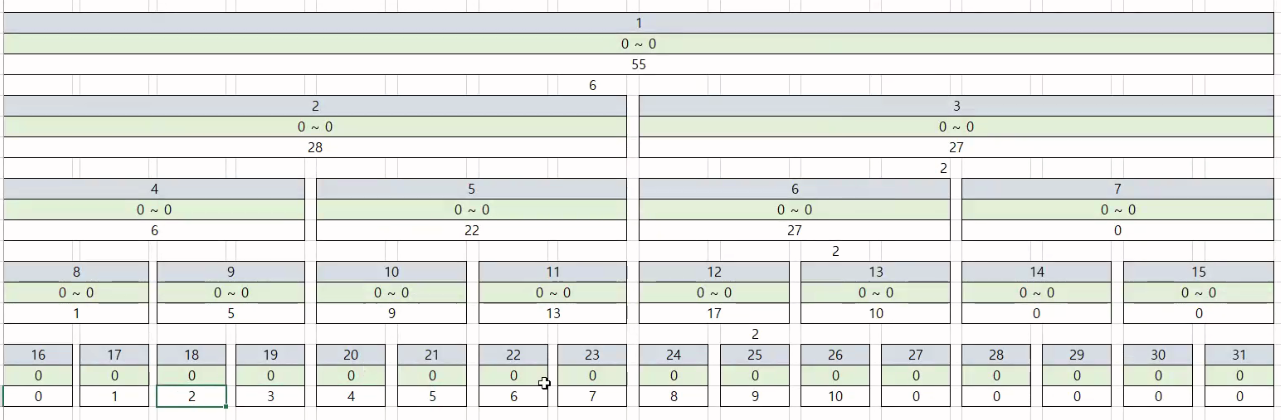
✔ 최초의 홀수/ 짝수 조상을 만난다 = 내가 원하는 구간을 벗어난는 범위를 가진 조상을 만난다. (사진보며 이해하자)

using namespace std;

#include <iostream>
#define MAX (1<<21)
#define PIV ((1 << 20)-1)
long long tree[PIV * 2];

void update(long long n, long long v) { //n번째 리프 노드값을 v로 바꾸기.
	n += PIV;
	tree[n] = v;
	//조상 노드들 값도 업데이트 하자
	while ((n = n / 2) > 0) { //조상에 다다를 때까지
		//내 윗 조상 = 왼쪽자식 + 오른쪽자식
		tree[n] = tree[n * 2] + tree[n * 2 + 1];
	}
}

long long query(long long l, long long r) { //l ~ r까지의 구간합
	l += PIV, r += PIV;
	long long ret = 0;
	while (l <= r) {
		if (l % 2 == 1) ret += tree[l++]; //l의 경우 최초의 홀수 조상의 노드를 만나면 tree[l+1]더하기
		if (r % 2 == 0) ret += tree[r--]; //r의 경우 최초의 짝수 조상의 노드를 만나면 tree[r-1] 더하기
		l /= 2, r /= 2;
	}
	return ret;
}
int main() {
	int n, m, k;
	long long a, b, c;

	cin >> n >> m >> k;
	for (int i = 1; i <= n; i++) {
		cin >> a;
		update((long long)i, a);
	}
	for (int i = 0; i < m + k; i++) {

		cin >> a >> b >> c;
		if (a == 1) update(b, c);
		else cout << query(b, c) << '\n';
	}

}