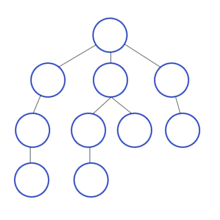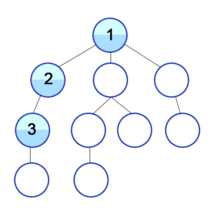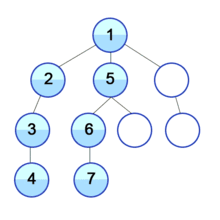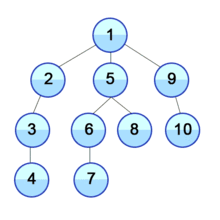
DFS (Depth-First Search)
: DFS는 맹목적 탐색방법의 하나로 탐색트리의 최근에 추가된 노드를 선택하고, 이 노드에 적용 가능한 동작자 중 하나를 적용하여 트리에 다음 수준(level)의 한 개의 자식노드를 추가하며, 추가된 자식 노드가 목표노드일 때까지 앞의 자식 노드의 추가 과정을 반복해 가는 방식이다.
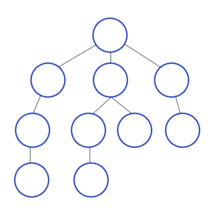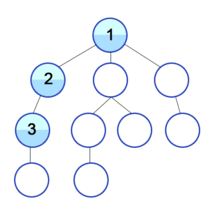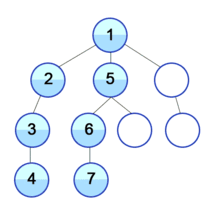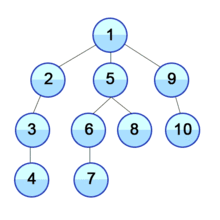
출처 : https://ko.wikipedia.org/wiki/%EA%B9%8A%EC%9D%B4_%EC%9A%B0%EC%84%A0_%ED%83%90%EC%83%89
1. 알고리즘
: 깊이 우선 탐색은 정점 v를 방문함으로써 시작된다.
다음으로 v에 인접하면서 아직 방문하지 않은 한 정점 w를 선택하여 이 w에서 다시 깊이-우선 탐색을 시작한다.
인접 정점들은 이미 모두 방문한 정점 u에 도달하면, 마지막으로 방문한 정점 중 아직 방문하지 않은 인접 정점 w를 가지고 있는 정점까지 되돌아가서 정점 w로부터 깊이-우선 탐색을 다시 시작한다.
이러한 탐색은 방문을 한 정점들로부터 방문하지 않은 정점으로 더 이상 갈 수 없을 때 종료된다.
2. Pseudo-code
virtual void Graph::DFS() //Driver
{
visited = new bool[n]; //visited는 Graph의 bool 데이타 멤버로 선언됨
fill(visitied, visitied+n, false);
DFS(0); //정점 0에서 탐색 시작
delete[] visited;
}
virtual void Graph::DFS(const int v) //workhorse
{ //정점 v에서 도달할 수 있는 모든 미방문 정점들을 방문
visitied[v] = true;
for(each vertex w adjacent to v) //실제 코드는 반복자를 사용
if(!visited[w])
DFS(w);
}3. 시간복잡도
: 그래프 G를 인접리스트로 표현할 경우 v에 인접한 정점들 w는 링크 체인을 따라가 결정할 수 있다.
DFS 알고리즘은 인접 리스트에 있는 노드들을 최대 한 번씩 조사하고, 리스트 노드의 수는 2e개 이므로 탐색을 완료하는 시간은 O(e)가 된다.
G를 인접 행렬로 표현했을 때 v에 인접한 모든 정점들을 결정하는 데는 O(n)의 시간이 걸린다.
최대 n개의 점을 방문해야 되므로 총 시간은 O(n^2)이다.
BFS (Breadth-First Search)
: 너비 우선 탐색(Breadth-first search, BFS)은 맹목적 탐색방법의 하나로 시작 정점을 방문한 후 시작 정점에 인접한 모든 정점들을 우선 방문하는 방법이다. 더 이상 방문하지 않은 정점이 없을 때까지 방문하지 않은 모든 정점들에 대해서도 너비 우선 검색을 적용한다. OPEN List는 큐를 사용해야만 레벨 순서대로 접근이 가능하다.
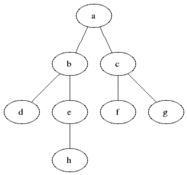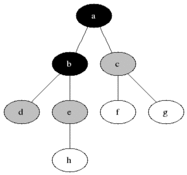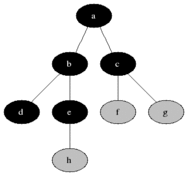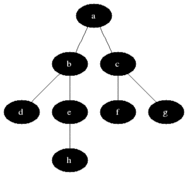
출처 : https://ko.wikipedia.org/wiki/%EB%84%88%EB%B9%84_%EC%9A%B0%EC%84%A0_%ED%83%90%EC%83%89
1. 알고리즘
: 너비-우선 탐색(BFS)은 시작 정점 v를 방문하는 것으로 시작한다.
다음으로 v에 인접한 방문하지 않은 모든 정점들을 방문한다.
그리고 다시 이 새로 방문한 정점들에 인접하면서 아직 방문하지 않은 정점들을 방문하는 방식으로 계속한다.
2. Pseudo-code
virtual void Graph::BFS(int v)
{ //너비-우선 탐색은 정점 v에서부터 시작한다.
//v를 방문하면 visitied[i]는 true로 설정된다. 이 함수는 큐를 이용한다.
visited = new bool[n];
fill(visited, visited +n, false);
visited[v] = true;
Queue<int> q;
q.push(v);
while(!q.IsEmpty())
{
v = q.Front();
q.Pop();
for(all verticies w adjacent to v) //실제 코드는 반복자를 사용
if(!visited[w])
{
q.push(w);
visited[w] = true;
}
}
delete [] visited;
}3. 시간복잡도
: 방문한 각 정점들은 큐에 오직 한 번만 들어가므로 while 루프는 최대 n번 반복된다.
인접 행렬이 사용되는 경우 방문하는 각 정점에 대해 루프는 O(n) 시간이 걸리므로 전체 시간은 O(n^2)이 된다.
인접 리스트가 사용되면 이 루프의 전체 비용은 d0 + ... + dn-1 = O(e)가 된다.
여기서 di는 정점 i의 차수이다.
DFS의 경우에서와 마찬가지로 방문한 모든 정점과 그것에 부속한 모든 간선들은 G의 연결요소가 된다.