conditional probability
the probability of one event calculated under the assumption that another event has occurred
let A,B events in S: P(A|B) is the probability of A given B, B is assumed to have occurred.
That is, A|B implies B occurs, A occurs only if A ∩ B occurs.
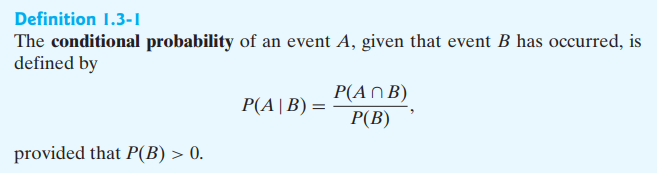
example
we have a batch of 100 parts where 15 are defective. Randomly select two parts without replacement.
let A1: "the 1st part is defective" and A2: "the 2nd part is defective"
1. Find the probability that the 2nd part is defective given that 1st is not defective.
2. Find probability that 2nd part is defective given 1st is defective.
3. what is the probability of 2nd part is defective?
풀이 방법 노트 참고
Independent events
Intuitively, two evnets are independent if knowing whether one event occurred(or did not) does not affect the probability of the other event will occur.
(i.e. the events don't contain information about each other = disjoint)

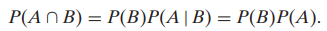
which also means that P(A) = P(A|B)
-
Suppose we call A is not-trivial if P(A)>0, two non-trivial events A&B are independent if and only if one of the following statements is true
1) P(A|B) = P(A)
2) P(B|A) = P(B)
3) P(A ∩ B) = P(A)*P(B)- if our probability model assumes independence, then we can assume statements 1) ~ 3) hold.
- if we went to show two events are independent, we need to show one of the three statements holds.
-
we can know whether event A and B are independent by comparing the result of P(A ∩ B) and P(A)*P(B)
-
In general, two events cannot be both independent and disjoint.

