[Algorithm]2차원 행렬 회전

AlBan·2021년 5월 20일

algorithm matrix rotate 알고리즘 행렬회전

Algorithm

목록 보기

3/4

Intro

가장 처음 행렬 회전을 요했던 문제는 백준의 Maaaaaaaaaze 문제 였다.

해당 문제에서는 2차원 배열을 회전하고, 회전한 배열을 다시 조합하여 길을 찾을 수 있는지 없는지에 대한 결과를 출력하는 문제였으며, 약간의 생각으로 간단하게 풀 수 있었다.

하지만, 최근에는 관련된 문제를 잘 안풀어서인지, 카카오 공채 코딩테스트에서 나온 문제인 자물쇠와 열쇠문제에서 제대로 구현해내지 못하고 헤매었고, 결국엔 풀어 냈기 때문에 정리차 포스팅을 한다.

행렬 회전

행렬의 회전은 사실 어려운 내용은 아니다. 머릿속의 시뮬레이션만으로 규칙을 찾아내는게 힘들다면, 종이와 펜을 준비해 그림을 그리고 유심히 본다면 규칙을 찾아낼 수 있다.

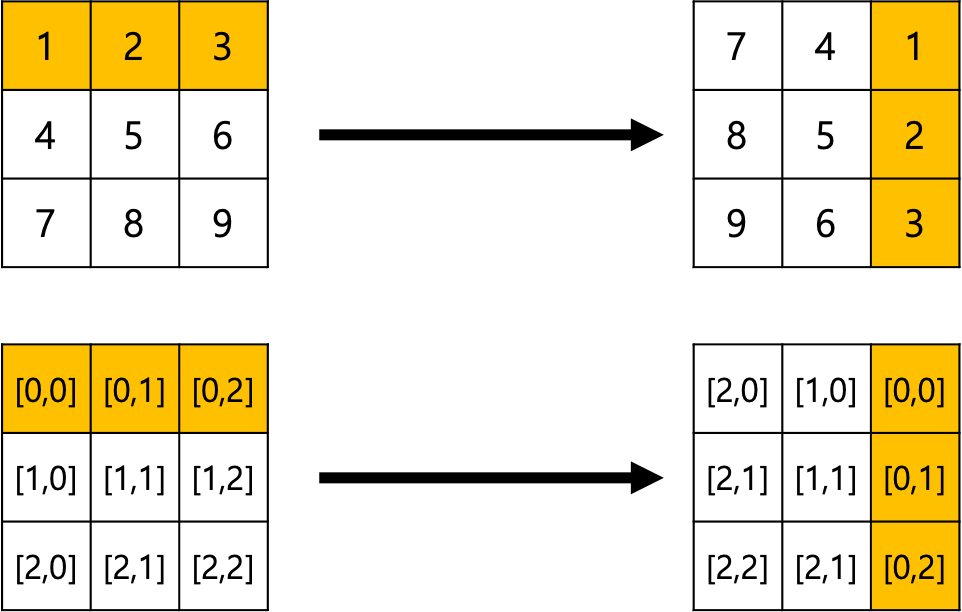
그림을 보면서 설명을 하자면, 다음과 같이 1~9까지 원소가 들어있는 $3 \times 3$ 행렬을 90도 회전시키려고 한다.
행렬 회전

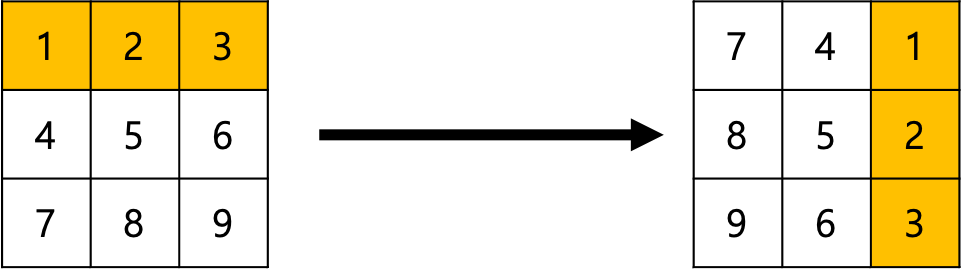
좀 더 알아보기 쉽게, 원소를 좌표값으로 바꾸면 다음과 같다.

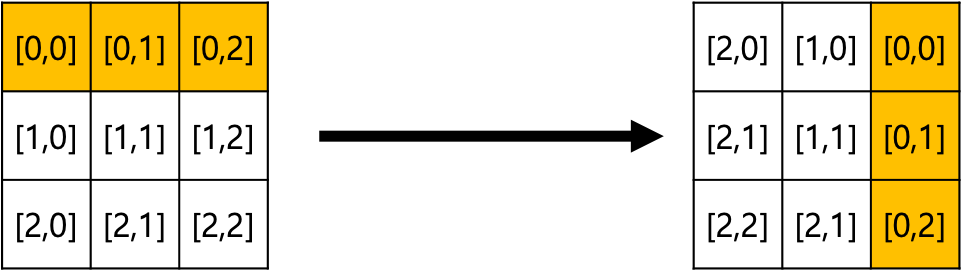
행렬 회전_좌표

[0, 0] 좌표의 원소가 [0, 2] 좌표로 옮겨갔고, [0, 1]좌표의 원소는 [1, 2]의 좌표로, [0, 2]는 [2, 2]의 좌표로 옮겨졌다.

정리하면,

[0, 0] ➡ [0, 2]
[0, 1] ➡ [1, 2]
[0, 2] ➡ [2, 2]

즉, 행렬의 길이가 N이라고 할 때, [y, x]은 [x, N - 1 - y]의 좌표로 옮겨지는 규칙을 발견할 수 있다.

행렬 회전의 규칙

before 배열의 x값 인덱스는 after 배열의 y값 인덱스로 바뀌고,
before 배열의 y값 인덱스는 after 배열의 N - i - 1 인덱스로 바뀐다.

그럼 위에서 발견하였던 규칙을 코드로 적용해보자.

행렬 회전 코드

위에서 발견한 규칙은 행렬의 원소 각 하나에 대해 적용할 수 있다. 그렇기 때문에, 원본 행렬의 모든 원소를 탐색하면서, 탐색한 원소의 인덱스에 규칙을 적용하여 얻은 좌표를 새롭게 생성할 행렬(회전이 적용된 행렬)에 적용하여 원소값을 대입시켜주어야 한다.

public static void main(){
	int[][] before = {{1,2,3}, {4,5,6},{7,8,9}};
    
	for(var arr : new Main().rotateMatrix(before){
		System.out.println(Arrays.toString(arr);
	}
}

public int[][] rotateMatrix(int[][] before){
	int N = origin.legnth;
	int[][] after = new int[origin.length][origint.length];
    
    for(int i = 0; i<N; i++){
    	for (int j = 0; j< N; j++){
        	after[j][N - i - 1] = before[i][j];
        }
    }

	return after;
}

180도 회전(flip)

위에서는 90도 회전에 대해서만 다뤘다. 행렬을 180도 회전(뒤집기)는 어떻게 할까?

물론, 90도 회전을 두번 실행하면 된다. 하지만, 행렬의 크기가 매우 클 경우 이렇게 나이브한 생각을 갖고 실행을 하면 낭패를 볼것이다. 그럼 역시, 규칙을 찾고 적용하는 방법이 가장 빠를것이다.

다시 그림을 보면서 규칙을 찾아보자

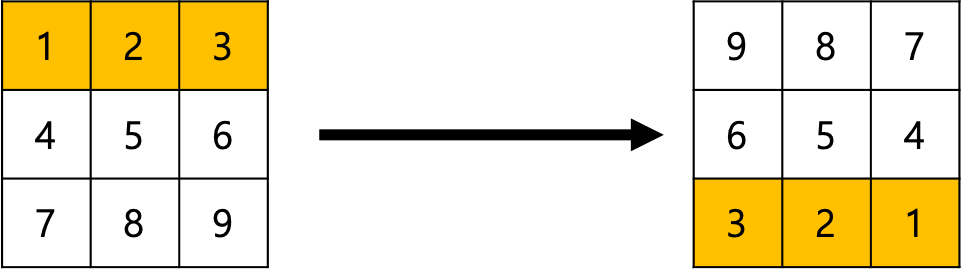
[0, 0] ➡ [2, 2]
[0, 1] ➡ [2, 1]
[0, 2] ➡ [2, 0]

위와같이 원소의 좌표가 변경되었다.
하지만 이정도로는 어떠한 규칙이 있는지 찾아내기 힘들다. 다른 좌표들 또한 어떻게 변경되었는지 확인해보자.

[1, 0] ➡ [1, 2]
[1, 1 ] ➡ [1, 1]
[1, 2] ➡ [1, 0]
[2, 0] ➡ [0, 2]
[2, 1 ] ➡ [1, 2]
[2, 2] ➡ [0, 0]

이제 규칙을 알아낼 수 있다.
Y좌표값은 전체 길이에서 자기 자신의 Y좌표를 뺀 값을, X좌표는 전체 길이에서 자기 자신의 X좌표를 뺀 값의 좌표를 갖는 곳으로 이동한다.

행렬의 좌표는 0부터 시작하므로, 전체 길이 N에서 1을 빼준값에서 각각 Y좌표값과 X좌표값을 빼주면 된다.

행렬 180도 회전(flip)의 규칙

y 좌표 값은 N - 1 - y로,
x 좌표는 N - 1 - x 좌표로 바뀐다.

코드

위에서 발견한 규칙을 기반으로 코드를 작성하면 다음과 같이 작성할 수 있다.

public int[][] flipMatrix(int[][] before){
	int N = origin.legnth;
	int[][] after = new int[origin.length][origint.length];
    
	for(int i = 0; i<N; i++){
		for (int j = 0; j< N; j++){
			after[N - 1 - i][N - 1 - j] = before[i][j];
		}
	}

	return after;
}