Inefficiency of the Base and Bound Approach
Base and Bound 문제점
한 프로세스의 address space를 physical memory로 mapping하면 address space의 Heap과 Stack 사이의 free space도 physical memory로 mapping된다.
-> physical memory의 낭비가 발생한다.
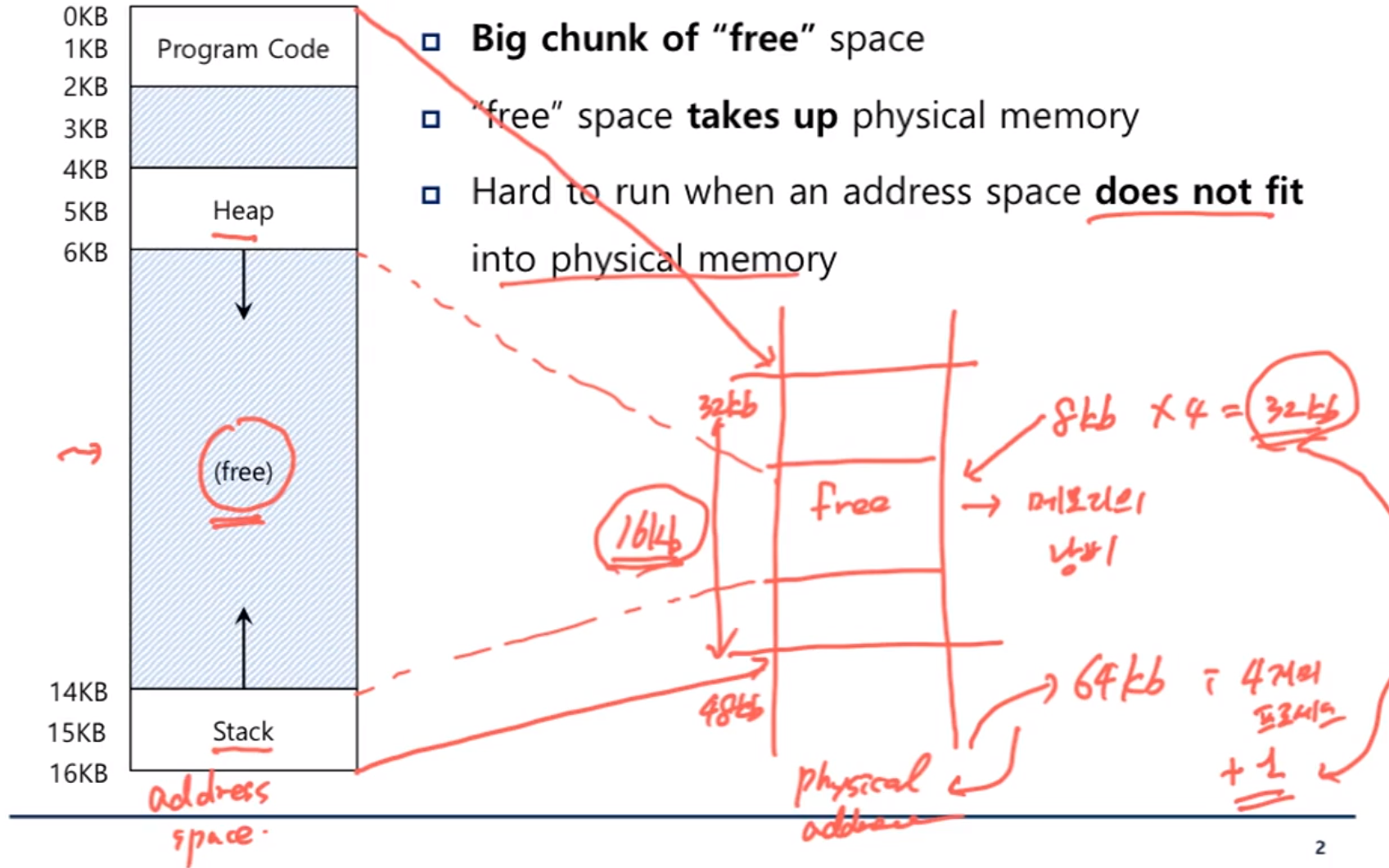
64KB의 physical address가 있다고 가정한다. 각각의 프로세스에는 대략 8KB의 free space가 존재한다. 4개의 프로세스가 physical address에 mapping된다면 32KB의 free space가 이 시스템에 존재하게 된다. 하지만 이러한 free space는 연속적인 공간이 아니어서 새로운 프로세스를 할당하지 못하는 문제가 발생한다.
Segmentation
Segment
address space에서 특정한 크기를 갖는 연속적인 주소공간
일반적으로 코드, 스택, 힙 세그먼트를 하나의 address space에서 가지게 된다.
각 세그먼트의 크기는 서로 달라도 되며, physical memory의 연속적인 공간에 놓이지 않아도 된다.
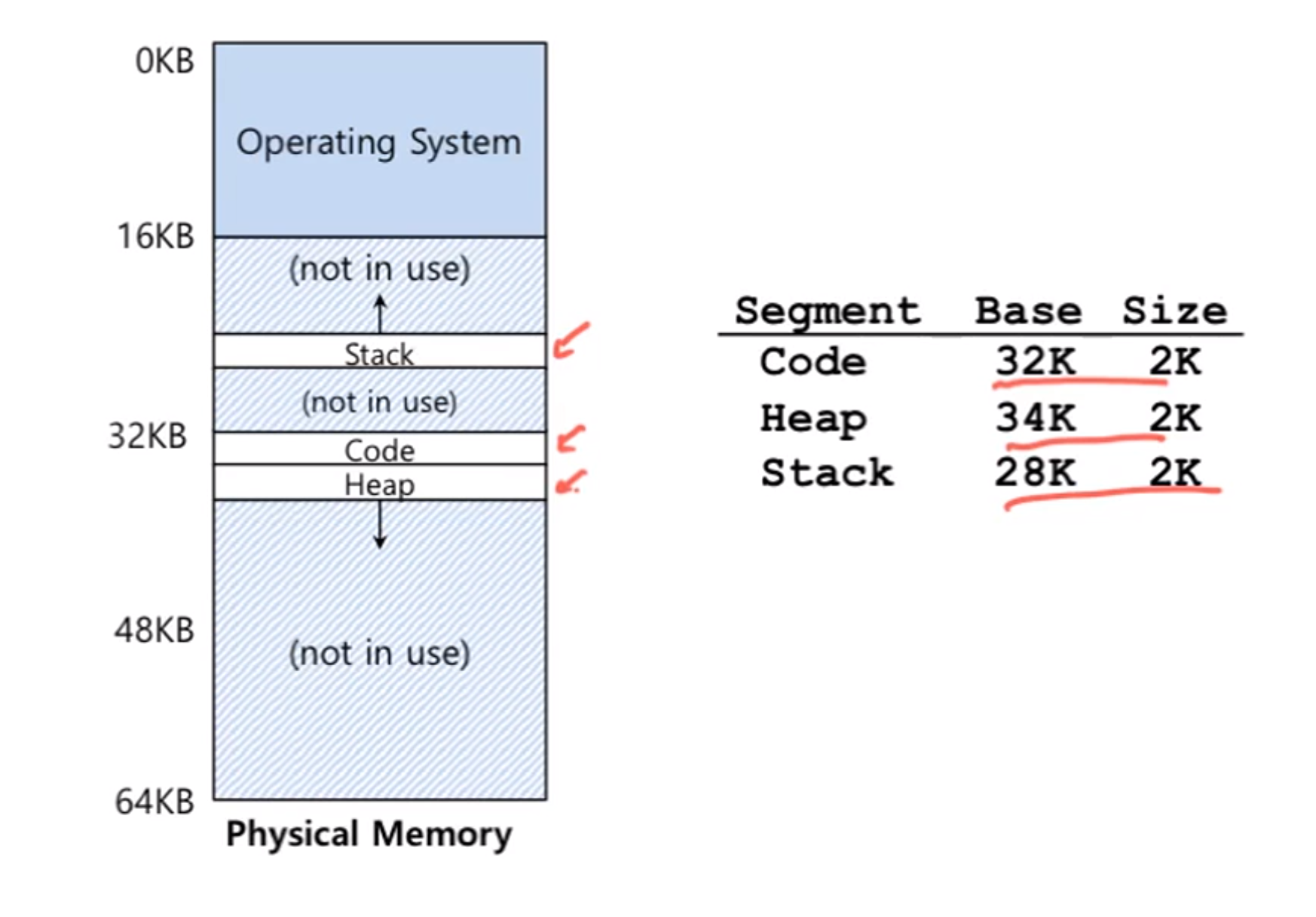
Base & Bound 기법에서 힙과 스택 사이의 free space를 메모리로 mapping하지 않아도 됨 -> physical memory 절약
Address Translation on Segmentation
physical address = Offset + Base
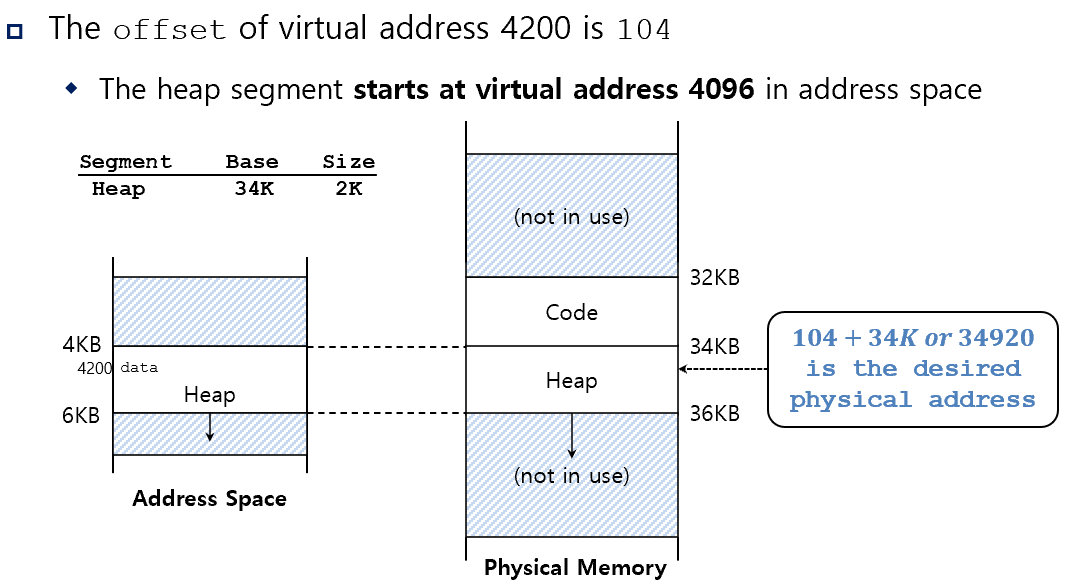
Offset = 4200 - (1024 * 4) = 104
Base = 34KB
physical address = 34KB + 104메모리 공간에 접근하다가 만약 7KB 주소에 접근하려고 하면 하드웨어가 허가받지 않은 공간임을 감지하고 운영체제에 Segmentation Fault를 발생시킨다.
Referring to Segment
Explicit approach
시스템 설계자들은 virtual address만 주어졌을 때, Offset과 Base 값을 빠르게 알기 위해서 Explicit approach를 개발했다.
4200번지를 Explicit approach에 맞게 가상주소로 변환해보자.
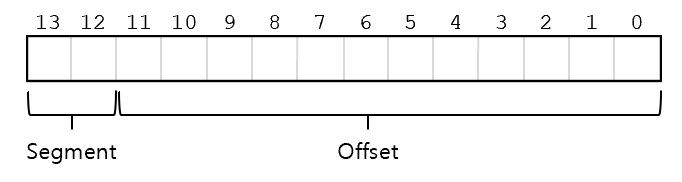
16KB = 2^14
0KB주소를 14비트로 표현 -> 00|000000000000
4KB주소를 14비트로 표현 -> 01|000000000000
8KB주소를 14비트로 표현 -> 10|000000000000
12KB주소를 14비트로 표현 -> 11|000000000000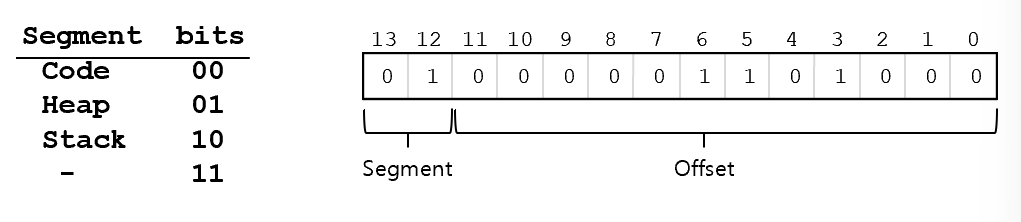
4200번지는 Heap영역에 소속되어 있는 번지이기 때문에 Segment는 01이 되어야 한다.
Offset은 104이며, 이진수로 바꾸면 00|000001101000이다
따라서, 4200번지를 Explicit approach로 표현하면 01|000001101000이 된다.
virtual address를 하드웨어가 어떻게 physical address로 변환하는지에 대해 pesudo로 보자.
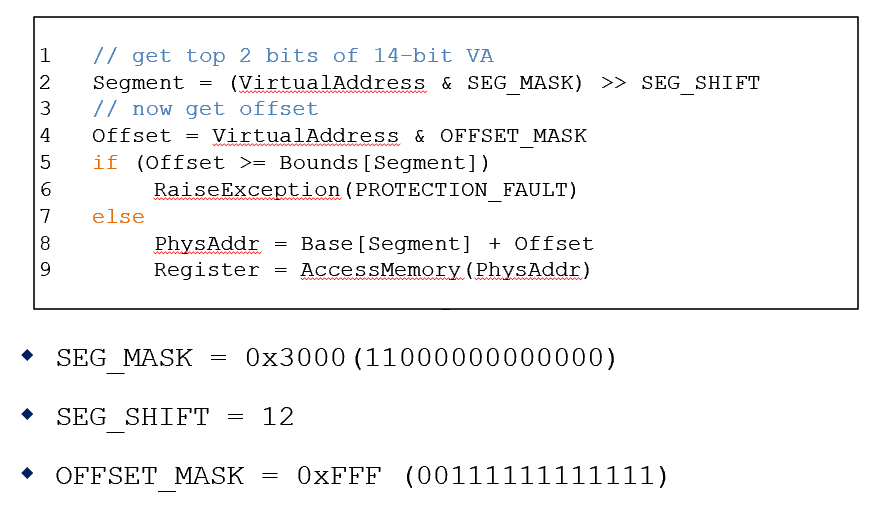
두번째 줄에서 virtual address와 SEG_MASK를 &연산하고, SEG_SHIFT만큼 오른쪽으로 SHIFT 하게 된다.
Segment
00|000001101000
&11|000000000000
----------------
01|00000000000001|000000000000 -> SEG_SHIFT -> 01|000000000000
-> Segment=01
Offset
01|000000000000
&00|111111111111
----------------
00|000001101000-> Offset=104
이제 relocation 정보를 보자.
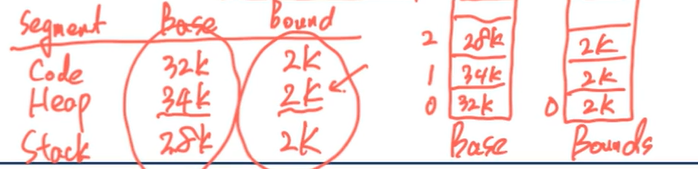
Heap의 경우 물리주소 34KB에 mapping이 되어있다.
Segment 하나의 최대 크기는 4KB이지만, Heap이 사용하는 Segment 크기는 2KB이다.
하드웨어는 Base와 Bound에 관한 정보들을 배열에 넣어서 저장하고 있다.
pseudo코드 5번째 줄을 보자.
여기에선 Segmentation Fault를 검사한다. 만약 Offset 값이 Segment의 Bounds를 넘었는지 검사한다.
Segment=01
Bound[Segment] = Bound[01] = 2KB
만약 Offset이 Bound[Segment]를 넘었는지 확인하고, 만약 넘었으면 허가받지 않은 공간에 접근하고 있는 거니 Segmentation Fault Error를 발생시킨다.
위에서 구한 Offset 값은 104이니 7번째 줄이 실행된다.
physical address를 계산하고 이 값을 통해 실제 물리 메모리에 접근하여 원하는 정보를 레지스터에 복사해 온다.
Referring to Stack Segment

Segmentation에서 Stack Segment의 physical address를 구하기 위해선 주의가 필요하다.
Stack은 주소가 증가하는 방향으로 자랄 수 있지만 감소하는 방향으로 자랄 수 있기 때문이다.
Stack의 특성을 지원하기 위해서 Extra hardware support가 필요하다.
하드웨어에서는 각각의 세그먼트가 자라는 방향을 기록할 수 있게 만든다.
Grow positive 1
physical address = Offset + Base
Grow positive 0
physical address = (Offset - Maximum_Segment_Size) + Base27KB의 Stack Data를 접근 (Grow positive = 0)
physical address = (3KB - 4KB) + 28KB = 27KB
Support for Sharing
Code sharing
하나의 프로그램을 가지고 여러 개의 프로세스를 만들면 만들어진 프로세스는 모두 같은 코드세그먼트 내용을 가지고 있다. Code sharing은 이러한 코드 세그먼트를 physical memory에 중복해서 놓는 게 아니라 sharing 기법을 통해서 하나의 코드 세그먼트를 공유해주게 하는 기법이다.

각각의 프로세스가 physical memory에 relocation 되면 1번과 4번 segment는 서로 내용이 같으니 physical memory에 중복해서 존재하는 것이 된다.
프로세스의 개수가 많아지면 중복되는 부분도 메모리에서 늘어나게 된다. 중복되는 코드세그먼트를 하나만 만들어놓고 여러 프로세스가 코드 세그먼트를 공유할 수 있게 한다면 물리 메모리의 사용량을 줄일 수 있다.
여기서 Code Segment는 Read-Execute 비트를 가져야 한다. 만약, Read-Write로 설정하면 같이 공유하고 있는 다른 프로세스가 코드의 내용을 바꿀 수 있고 그렇게 되면 프로그램 수행에 문제가 생긴다.
Fine-Grained and Coarse-Grained Segmentation
Coarse-Grained Segmentation은 하나의 프로세스에 관하여 작은 수의 세그먼트(보통 Code Segment, Heap Segment, Stack Segment)를 분할하는 것이며, Fine-Grained Segmentation은 세그먼트 개수 제한 없이 프로세스가 필요한 만큼의 세그먼트로 분할하는 것이다.
Fine-Grained Segmentation에서 많은 수의 세그먼트를 지원하기 위해서는 여러 세그먼트의 정보를 메모리에 저장할 수 있는 세그먼트 테이블 같은 하드웨어가 필요하다.
OS support: Fragmentation
External Fragmentation: 외부 단편화

physical memory에 24KB의 free space가 존재한다. 프로세스에서 20KB의 세그먼트를 할당해달라고 요청하게 되면 physical memory에서 연속적인 20KB의 공간을 찾을 수 없어 relocation 하지 못하는 문제가 발생하게 된다. 이러한 상황을 외부 단편화라고 한다.
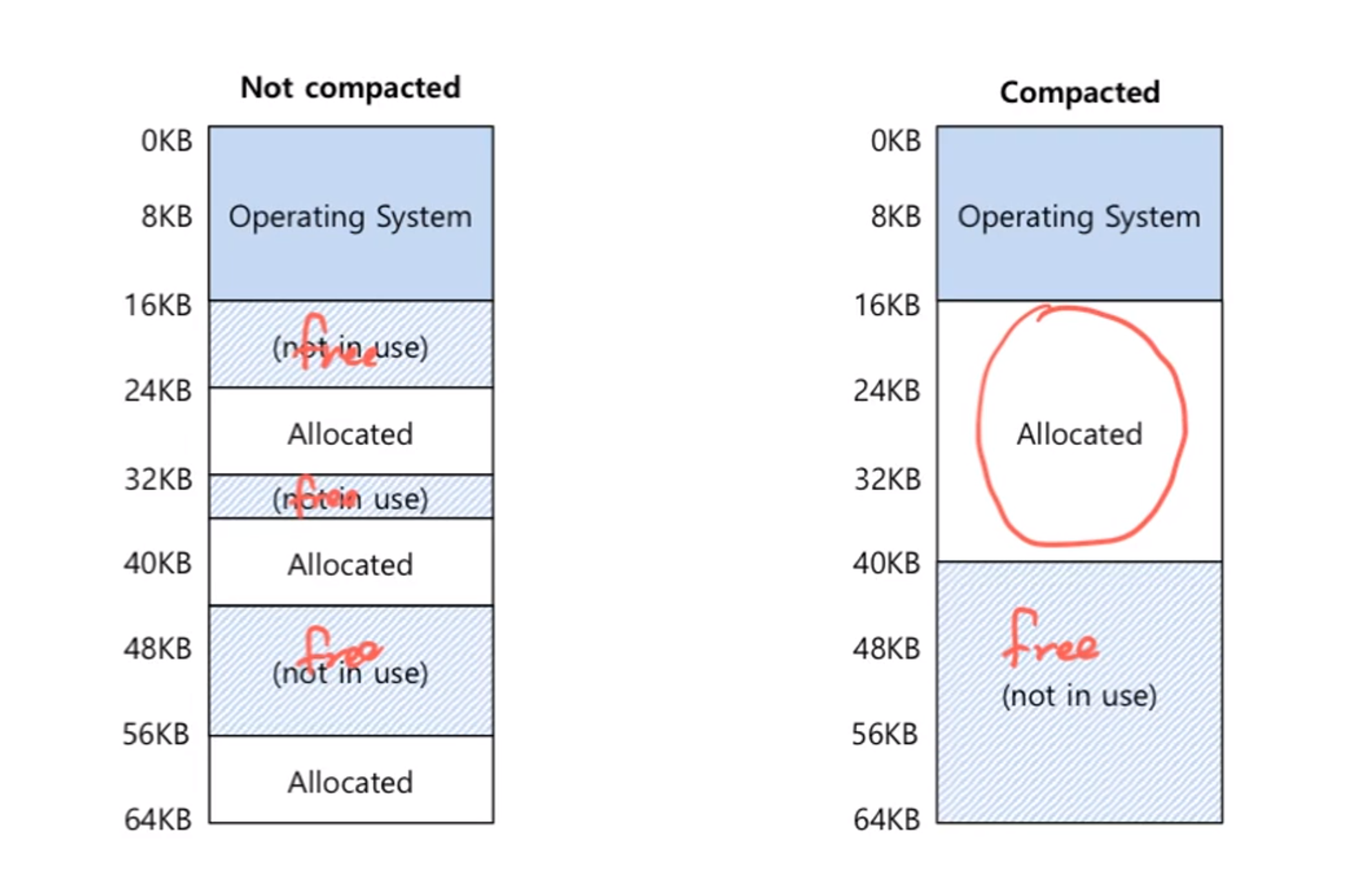
Compaction: 기존에 존재하던 세그먼트를 재배열한다.
1. 물리 메모리에 프로세스들이 접근하지 못하도록 프로세스를 멈춘다.
2. 데이터를 복사해서 physical memory에서 세그먼트를 옮긴다.
3. relocation 정보를 업데이트해 주어야 한다.
외부 단편화 문제는 해결될 수 있으나, 이 과정에서 프로세스의 성능이 크게 떨어질 수 있다.

와우@!