딥러닝이란?

🥚 딥러닝이란?

---

딥러닝은 컴퓨터가 데이터로부터 패턴을 배우는 방법 중 하나로 인간의 뇌에서 영감을 받은 것입니다.

딥러닝은 마치 마법과 같습니다.

한 마법사가 있고, 그에게는 마법봉이 있습니다. 마법사가 다양한 물건과 동물, 그리고 이상한 표지판들로 가득 찬 마을에 왔습니다. 그 마을에는 각각 다른 의미를 가진 여러 표지판들이 있습니다. 어떤 표지판은 맛집이 있는 곳을 가리키고, 다른 표지판은 범죄 소굴로 안내합니다.

마법사는 봉을 통해 표지판들을 읽고, 이 마을의 모든 비밀을 알아내기 시작합니다. 그는 봉을 흔들고, 표지판들을 읽는다. 그러면서 각 표지판의 뜻을 이해하고 마을을 더 잘 이해하게 됩니다.

여기서 마법사가 딥러닝의 모델입니다, 마법봉은 데이터의 패턴을 학습하는 도구, 표지판들은 데이터, 그리고 표지판이 가리키는 정보들이 데이터의 패턴입니다.

딥러닝 모델은 데이터를 통해 패턴을 찾아내고, 이것은 마법사가 마을의 표지판을 통해 비밀을 해독하는 것과 비슷합니다. 모델은 데이터를 보면서 점차적으로 더 높은 수준의 패턴을 파악하게 됩니다. 마법사가 더 많은 마을을 탐험하면서 봉을 더 많이 흔들어 경험을 쌓듯이, 딥러닝 모델도 더 많은 데이터로 학습하고 경험을 통해 더 나은 예측을 하게 됩니다.

대중에 알려진 딥러닝은 대표적으로 알파고가 있습니다. 이미지에서 얼굴을 찾아내거나, 음성을 이해하거나, 알파고와 같이 게임을 이해하고 사람을 이길 수 있는 것 같이 다양한 문제를 해결하는데 사용됩니다.

🐣 딥러닝의 기초: 선형 모델의 한계

처음에 배운 선형회귀와 논리회귀는 1차 함수를 사용하여 데이터를 모델링합니다. 이러한 선형 모델은 많은 문제에 적용 가능하지만, 현실 세계의 많은 문제는 직선 하나로는 설명할 수 없는 문제들이 훨씬 많습니다.

이 문제를 해결하기 위해, 선형 회귀를 여러 번 반복하여 비선형성을 추가하려고 시도했지만, 이렇게 반복해도 결과는 여전히 선형적이었습니다. 여러 번의 선형 변환을 쌓아도 결국 선형 변환으로 표현됩니다.

그래서 선형회귀 사이에 비선형성을 추가해야 한다고 판단했습니다. 이를 위해 층(Layer)을 여러 개 쌓아보았고, 이런 다층 구조로 모델을 구성하니 데이터를 더 잘 이해하고 복잡한 문제를 풀 수 있게 되었습니다. 층을 깊게 쌓는 것으로 "딥러닝(Deep Learning)"이라는 용어가 만들어졌습니다.

• 딥러닝의 다른 용어 표현

1. 딥러닝(Deep learning) : 가장 널리 사용되는 용어로, 다층 구조의 신경망을 통해 복잡한 패턴을 학습하는 기술
2. Deep neural networks : 딥러닝을 구성하는 다층 신경망 구조
3. Multilayer Perceptron(MLP) : 여러 층으로 구성된 신경망

• 딥러닝의 주요 개념과 기법
  • 배치 사이즈와 에폭 : 모델 학습 시 데이터를 어떻게 나누어 학습시키는지와 학습 횟수를 정의합니다.
  • 활성화 함수 : 뉴런의 활성화를 조절하는 함수로, 비선형성을 추가하여 모델의 표현력을 향상시킵니다.
  • 과적합과 과소적합 : 모델이 너무 복잡하면 과적합이 발생하고, 너무 단순하면 과소적합이 발생합니다. 최적의 모델을 만들기 위한 기법들이 필요합니다.
  • 데이터 증강 : 데이터를 인위적으로 확장하여 모델의 성능을 향상시키는 방법입니다.
  • 드랍아웃 : 학습 중에 일부 뉴런을 무작위로 비활성화하여 모델을 더 견고하게 만드는 기법입니다.
  • 앙상블 : 여러 모델을 결합하여 성능을 향상시키는 기술입니다.
  • 학습률 조정 : 학습률을 동적으로 조절하여 모델의 수렴 속도와 성능을 최적화하는 방법입니다.

🐤 딥러닝의 역사

머신러닝의 초기 단계에서는 AND, OR와 같은 간단한 논리 문제를 풀면서 시작했습니다.

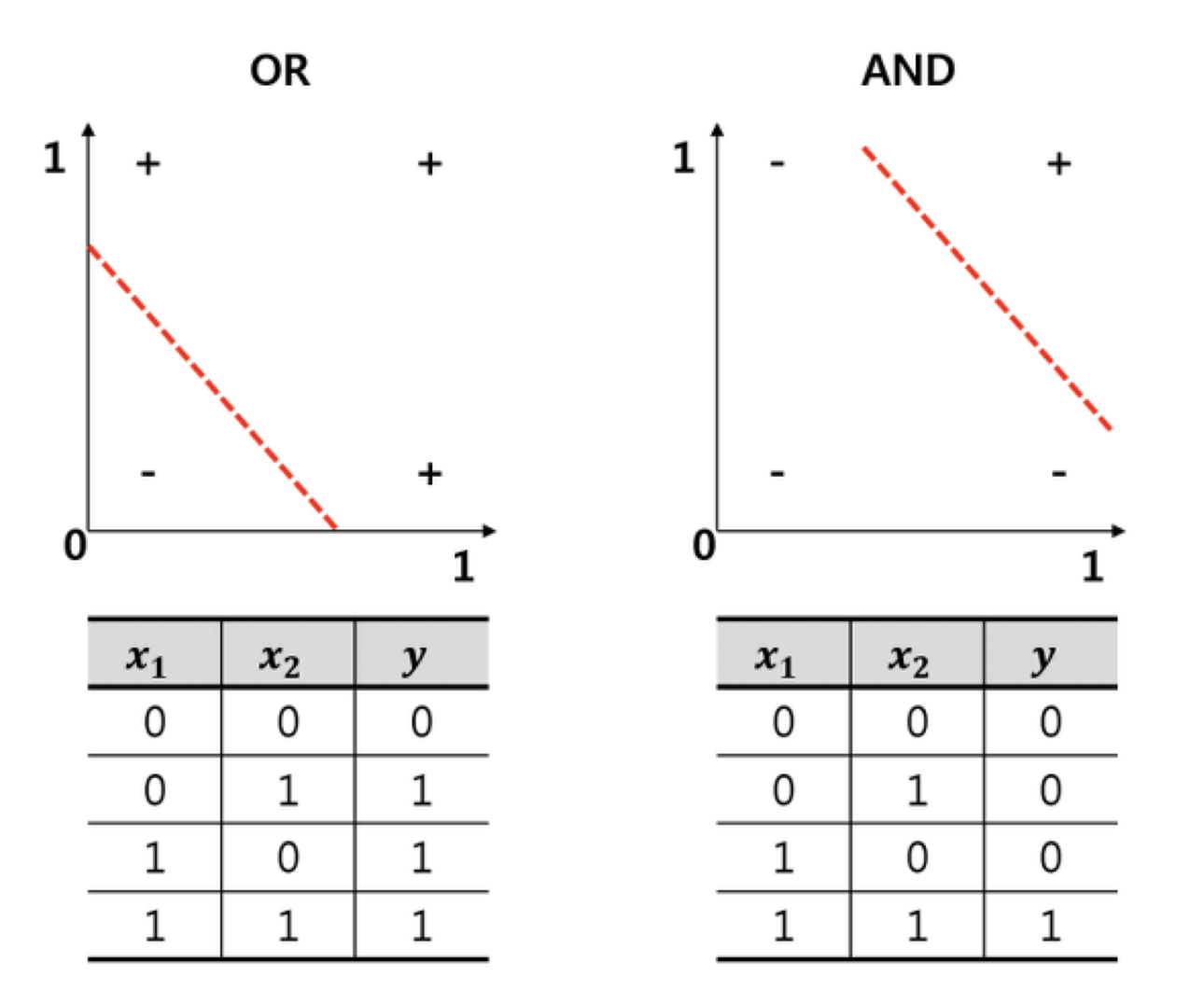
이러한 문제는 선형 함수를 사용하여 쉽게 해결할 수 있었습니다. 예를 들어, AND 논리 연산은 선형 함수로 쉽게 모델링할 수 있는데, 이를 퍼셉트론(Perceptron)이라고 부릅니다.

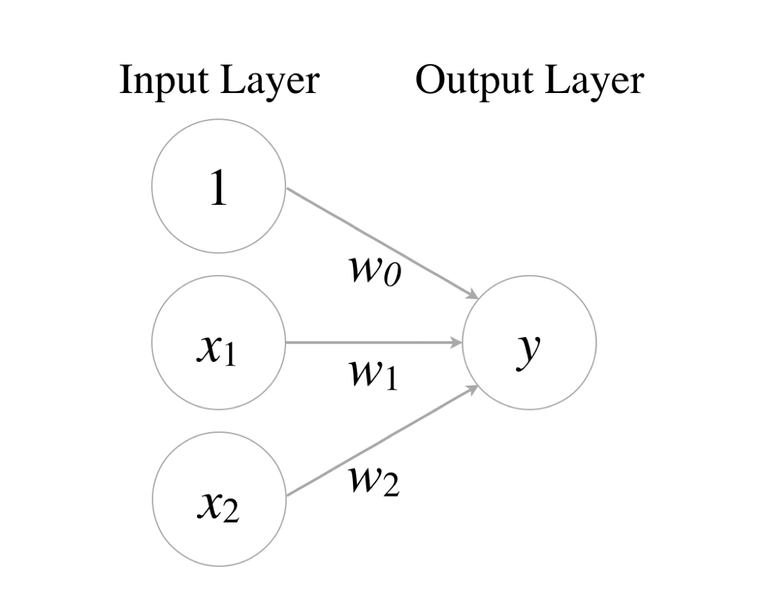
위와 같이 w0, w1, w2 의 값만 잘 지정해주면 원하는 출력을 계산할 수 있었기 때문에 AND, OR 문제를 잘 조합하면 생각하는 기계를 만들 수 있겠다는 생각을 하게 됩니다.

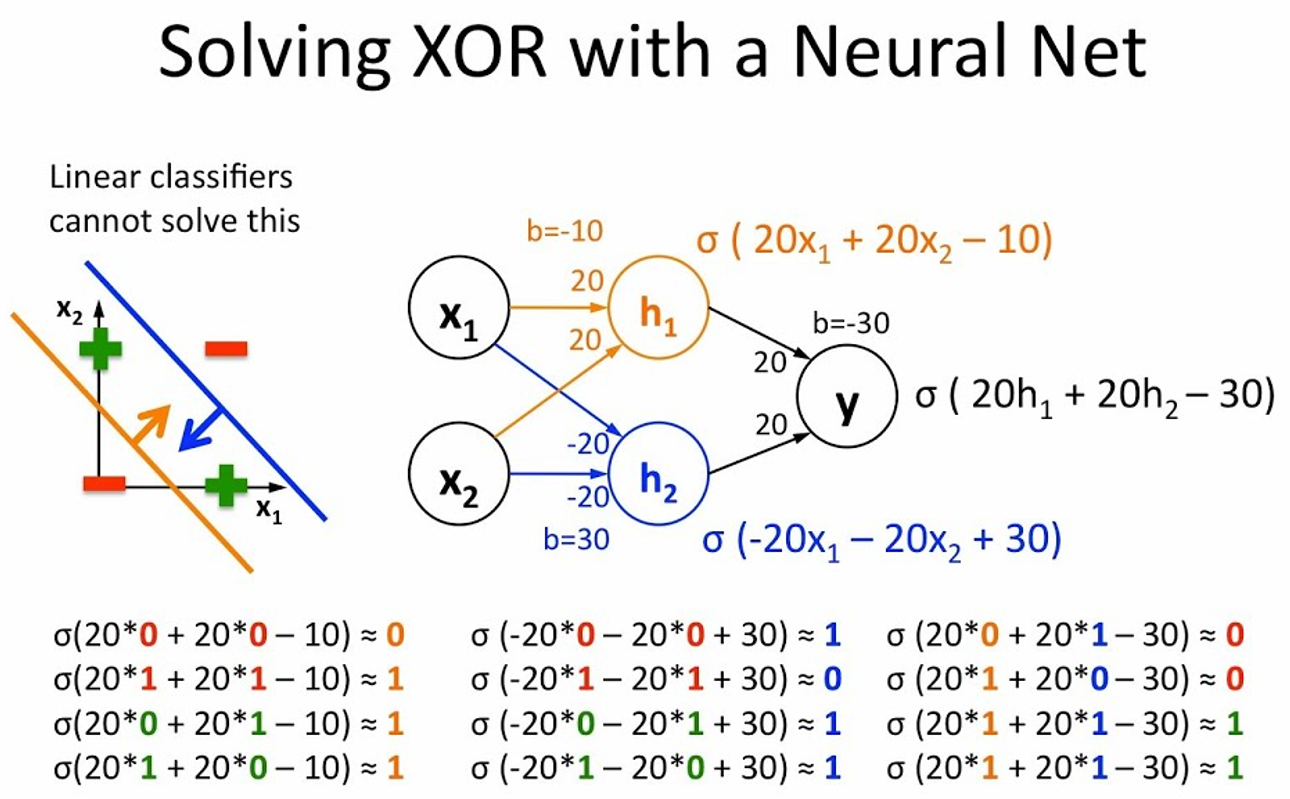
그러나 XOR 문제와 같이 입력값을 비선형적으로 분리해야 하는 경우, 단순한 퍼셉트론과 선형 모델만으로는 문제를 해결할 수 없었습니다.

• XOR(배타적 논리합) 문제
  두 개의 이진(binary) 입력값(0 또는 1)을 받아 하나의 출력값을 반환하는 것을 목표로 하고 입력 A와 B 중 하나만이 1일 때 결과가 1이 되는 것으로, 비선형적인 관계를 갖는 문제입니다.

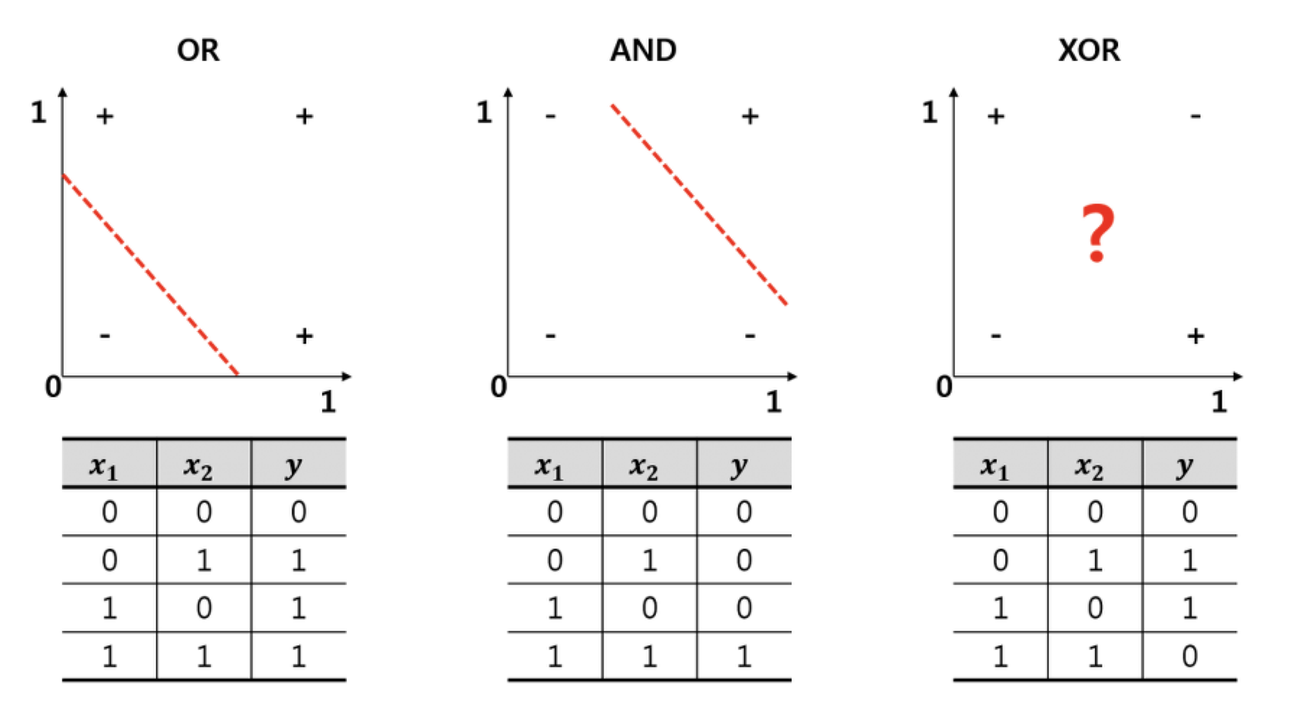
선형 모델의 경우, 출력 변수의 변화는 입력 변수의 변화에 비례하여 직선 형태로 나타납니다. XOR 연산의 결과는 불연속적인 값(0 또는 1)을 가집니다. 선형 모델은 연속적인 값에 대한 회귀나 분류에는 적합하지만, "하나만 1이면 1"과 같이 입력 변수를 비선형적으로 분리하는 비선형 논리 관계를 나타내기 어렵습니다. 즉, 불연속적인 결과를 직선으로 정확하게 모델링하기 어렵습니다.

그래서 XOR 연산과 같은 비선형 논리를 정확하게 모델링하기 위해서 Perceptron을 여러개 붙인 MLP(Multilayer Perceptrons)와 같은 다층 신경망이라는 개념을 도입해서 문제를 풀어보려고 했습니다.

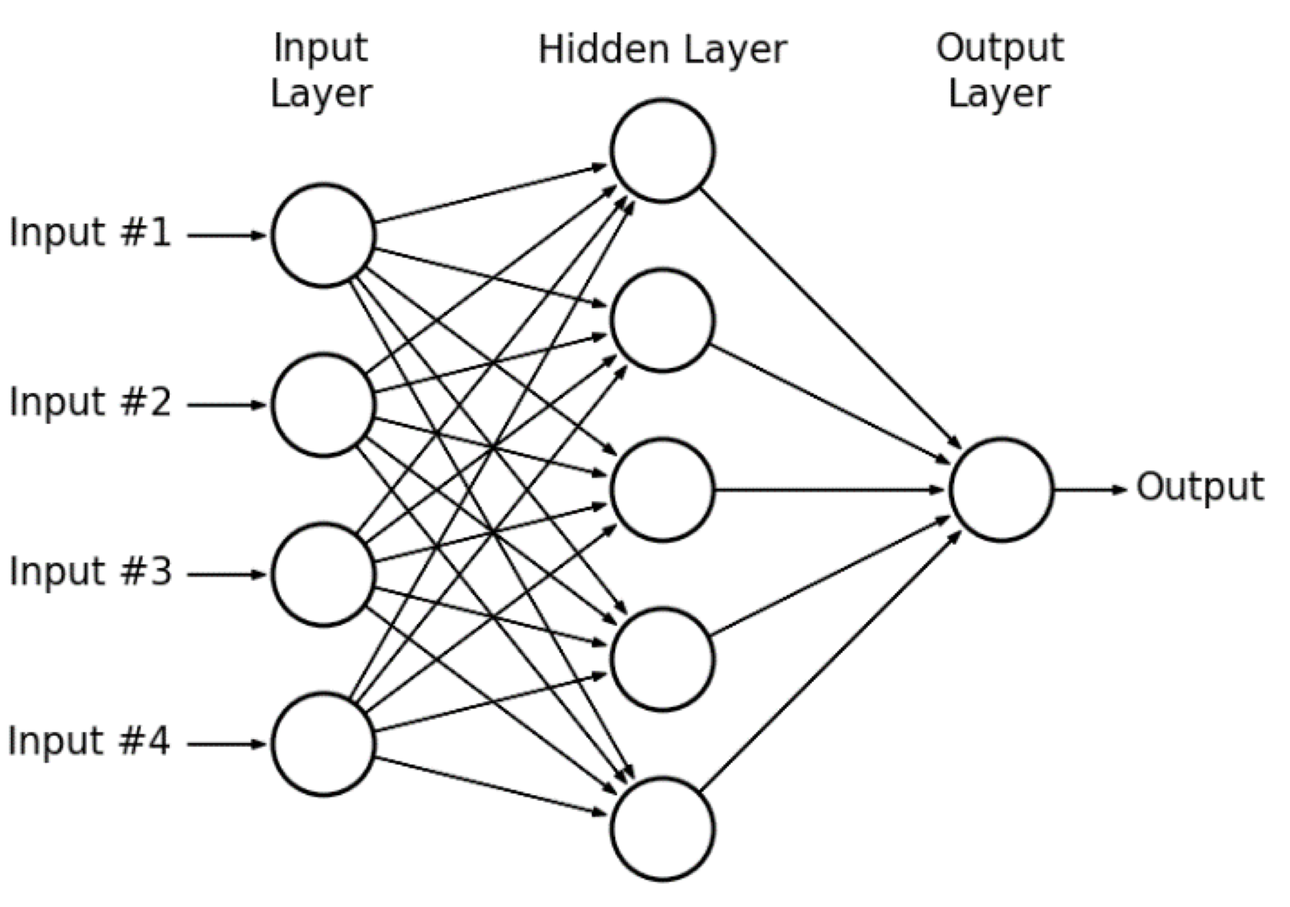
그러나 많은 사람들이 MLP로 XOR 문제를 풀기 위해 도전했지만 Marvin Minsky는 하나의 Perceptron으로는 XOR 문제를 해결할 수 없다고 주장했습니다. 그는 MLP를 사용해야 하지만, 각각의 weight와 bias를 학습시키는 데 너무 많은 계산이 필요하고 당시의 기술로는 불가능하다고 주장했습니다. 이러한 주장으로 인해 많은 사람들이 딥러닝 분야에서 비관적으로 돌아섰고, 딥러닝의 발전은 일시적으로 후퇴하게 되었습니다.

🐥 딥러닝의 후발주자와 역전파(Backpropagation) 알고리즘의 등장

계속 되어온 딥러닝의 침체기는 1974년에 발표된 Paul Werbos(폴)이라는 사람의 박사 논문 덕분에 끝이 나게 됩니다. 그의 주장은 이렇습니다.

1. 우리는 가중치(weight)와 편향(bias)를 이용해서 주어진 입력을 가지고 출력을 만들어 낼 수 있다.
2. 그런데 MLP가 만들어낸 출력이 정답값과 다를 경우 W와 b를 조절해야한다.
3. 그것을 조절하는 가장 좋은 방법은 출력에서 Error(오차)를 발견하여 뒤에서 앞으로 점차 조절하는 방법이 필요하다.

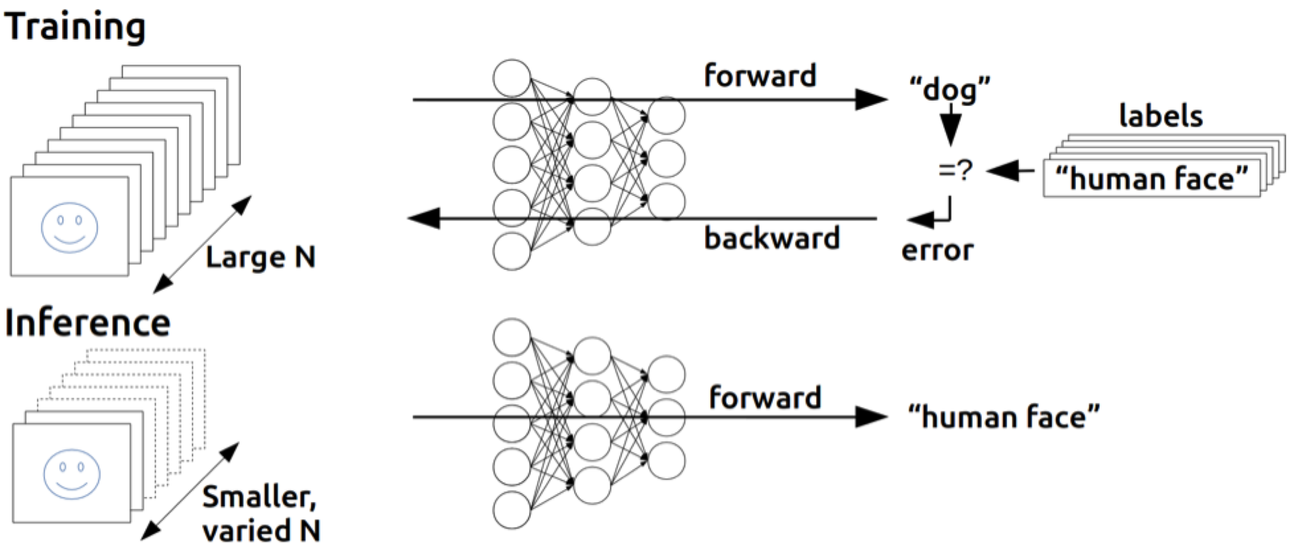
=> 출력(dog)이 정답값(human Face)와 다를 경우, 모델이 잘못 예측했으니 다시 돌아가서 weight와 bias를 조절

- 가중치(weight)

가중치는 입력 데이터에 대한 중요도를 나타내는 매개변수입니다. 입력층 데이터를 다음 노드로 넘길 때, 각 입력 데이터는 해당 가중치와 곱해지고(중요도를 적용) 이 곱샘 결과가 신경망의 뉴런에 전달됩니다. 가중치는 각 연결마다 고유하게 설정되며, 학습 과정에서 신경망이 입력 데이터를 올바르게 처리하도록 조정합니다. 만약 가중치(중요도)가 없다면 신경망에 전달되는 값은 모두 같을 것입니다. 게임 랭킹으로 예를 들면, 랭킹이 입력 데이터이고 전적이 가중치가 될 것입니다. 따라서, 가장 최근 전적에 대한 중요도를 가장 높다고 보고 최근 전적을 적용한 게임 랭킹을 알 수 있습니다.

- 편향(bias)

편향은 뉴런이 활성화되는 임계값을 조절하는 매개변수입니다. 쉽게 예를 들면, 옷을 사고 싶어하는 A와 B가 있다고 해봅시다. 이 둘의 중요도가 같다고 가정하기 위해 둘 다 사고 싶은건 꼭 사야하는 성격이라고 해보겠습니다. A는 저축을 통해 돈을 모아서 옷을 사려고 하고 있고, B는 일단 지르고 보자는 생각을 하고 있습니다. 이럴 경우 둘이 옷을 사는 과정에 대한 결과가 결코 같다고 볼 수 없습니다. 이때, 추가해주는 것이 바로 편향(성향 = b)입니다.

이 알고리즘으로 XOR 문제는 개선된 MLP로 풀 수 있게 되어 해결될 수 있었고 그 핵심 해결 방법은 바로 역전파 알고리즘의 발견이었습니다.

이러한 발전으로 딥러닝은 다시 주목받기 시작하며, 다층 신경망을 기반으로한 복잡한 문제들을 풀어내는 데 성공하였습니다. 딥러닝은 이후 계속해서 성장하고 발전하여 현재는 많은 분야에서 활용되고 있으며, 머신러닝 분야의 중요한 분야 중 하나로 자리 잡게 되었습니다.

🐓 Deep Neural Networks 구성 방법

---

앞서 나온 것처럼 딥러닝은 다양한 데이터와 복잡한 문제를 모델링하기 위해 여러 층의 인공 신경망을 쌓는 방식으로 이루어집니다.

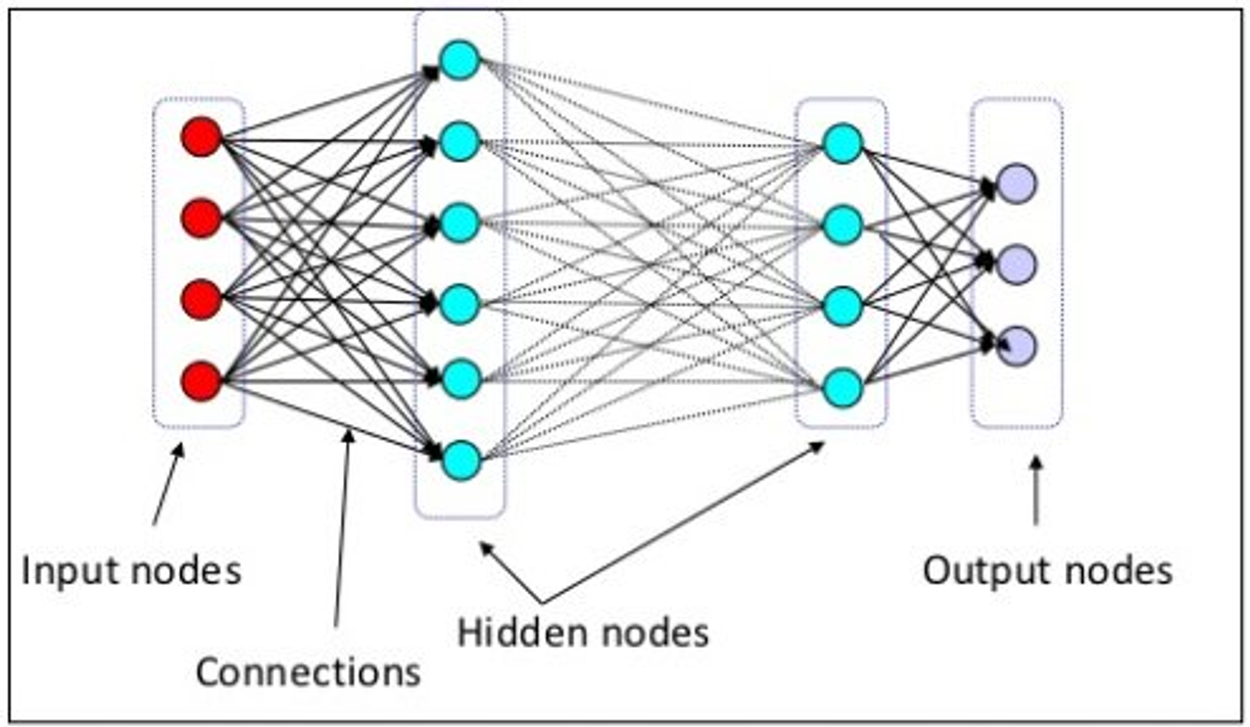
딥러닝에서 네트워크의 구조는 크게 3가지로 나누어집니다.

1. Input layer(입력층) : 네트워크의 시작점인 입력 부분으로 학습시키고 싶은 x 값을 입력합니다. 이 층은 데이터의 특성을 나타내며, 입력 데이터의 특성 수에 따라 입력 뉴런의 수가 결정됩니다.

2. Output layer(출력층) : 딥러닝 모델의 마지막 부분인 출력 부분으로, 모델의 최종 예측 값인 y 값입니다. 이진 분류에서는 하나의 뉴런을 사용하고, 다중 클래스 분류에서는 클래스 수와 동일한 수의 뉴런을 사용합니다.

3. Hidden layers(은닉층) : 딥러닝에서 가장 중요한 부분 중 하나는 여러 개의 은닉층을 쌓는 것입니다. 은닉층은 입력층과 출력층 사이에 위치하며, 각 은닉층은 여러 개의 뉴런으로 이루어져 있습니다. 은닉층은 데이터의 추상적인 특징을 학습하고 복잡한 패턴을 인식하는 역할을 합니다. 은닉층은 비선형성을 도입하여 모델이 비선형 관계를 학습할 수 있게 합니다.

• 활성화 함수 : 각 뉴런은 활성화 함수를 사용하여 입력을 출력으로 변환합니다. 이 활성화 함수는 은닉층 바로 뒤에 위치하여 활성화를 조절하고 비선형성을 도입하여 네트워크가 비선형 관계를 학습할 수 있게 합니다.
  

• 손실 함수 : 이 손실 함수는 모델의 예측과 실제 값 사이의 차이를 측정하고, 학습 중에 이 차이를 최소화하기 위해 가중치와 편향을 조절합니다.

입력층과 출력층의 모양은 풀어야하는 문제에 따라 정해져 있습니다. 입력층은 주로 모델에 입력되는 데이터의 특성 수에 따라 결정됩니다. 예를 들어, 이미지를 다루는 경우 이미지의 크기나 색상 채널 수에 따라 입력층의 노드 수가 정해집니다. 출력층은 모델이 수행하는 작업에 따라 달라집니다. 이진 분류 문제에서는 하나의 뉴런을 사용하고, 다중 클래스 분류 문제에서는 클래스 수에 맞는 뉴런을 가지게 됩니다. 회귀 문제에서는 출력층에 하나의 뉴런이 있고 연속적인 수치 값을 출력합니다.

은닉층은 데이터의 추상적인 특징을 학습하고 복잡한 패턴을 인식하는 데 사용됩니다. 이 층은 여러 개의 뉴런(또는 노드)으로 구성되며, 각 뉴런은 입력과 가중치를 곱하고 활성화 함수를 통과하여 출력값을 계산합니다. 뉴런들은 서로 연결되어 있으며 이를 통해 복잡한 관계를 학습할 수 있습니다.

은닉층의 넓이는 모델의 표현력을 결정하는 중요한 요소 중 하나입니다. 일반적으로, 은닉층을 더 넓게 만드는 것은 더 많은 뉴런을 포함하는 것을 의미하며, 이는 모델이 데이터의 복잡한 패턴을 학습할 수 있도록 돕습니다. 더 많은 뉴런을 사용하면 모델은 데이터의 다양한 특징을 포착하고 다룰 수 있게 됩니다. 예를 들어, 첫 번째 은닉층에 8개의 뉴런, 두 번째 은닉층에 16개의 뉴런, 세 번째 은닉층에 8개의 뉴런을 사용하는 것이 가능합니다. 이러한 구성은 모델이 데이터를 효과적으로 학습하고 표현하도록 돕습니다.

활성화 함수는 주로 은닉층 바로 뒤에 위치합니다. 이 위치에서 활성화 함수가 적용되면 뉴런의 선형 조합의 결과를 비선형 출력으로 변환합니다. 이것은 신경망이 데이터의 복잡한 관계를 학습할 수 있게 합니다.

네트워크의 Width(너비)와 Depth(깊이)

실무에서는 네트워크의 너비와 깊이를 바꾸면서 실험을 많이 합니다. 더 넓은 네트워크는 다양한 데이터 패턴을 학습할 수 있고, 더 깊은 네트워크는 데이터의 복잡한 계층적 패턴을 학습할 수 있습니다. 이로 인해 모델은 더 정확한 예측을 할 수 있습니다.

적당한 연산량을 가진, 적당한 정확도의 딥러닝 모델이 있다고 가정합시다.

모델의 크기는 다음과 같습니다:

• 입력층: 4
• 첫 번째 은닉층: 8
• 두 번째 은닉층: 4
• 출력층: 1

다양한 문제에 최적화된 모델 아키텍처를 찾기 위해 모델의 너비와 깊이를 가지고 테스트를 할 수 있는데

1. 네트워크의 너비를 늘리는 방법
   네트워크의 은닉층의 개수를 그대로 두고 은닉층의 노드 개수를 늘리는 방법입니다. 예를 들어, 너비를 베이스라인 모델의 2배로 늘리는 실험을 하겠다고 하면 아래와 같습니다.

• 입력층: 4
• 첫 번째 은닉층: 8 * 2 = 16
• 두 번째 은닉층: 4 * 2 = 8
• 출력층: 1

2. 네트워크의 깊이를 늘리는 방법
   네트워크의 은닉층의 개수를 늘리는 방법입니다.

• 입력층: 4
• 첫 번째 은닉층: 4
• 두 번째 은닉층: 8
• 세 번째 은닉층: 8
• 네 번째 은닉층: 4
• 출력층: 1

3. 너비와 깊이를 전부 늘리는 방법
   위에서 했던 두 가지의 방법을 모두 사용합니다.

• 입력층: 4
• 첫 번째 은닉층: 8
• 두 번째 은닉층: 16
• 세 번째 은닉층: 16
• 네 번째 은닉층: 8
• 출력층: 1

노가다 작업이기는 하지만 과적합과 과소적합을 피하기 위해서나 모델의 성능 향상을 위해서는 꼭 필요한 작업입니다.

🐔 딥러닝의 주요 개념

---

1. Batch size, Epoch (배치 사이즈, 에폭)

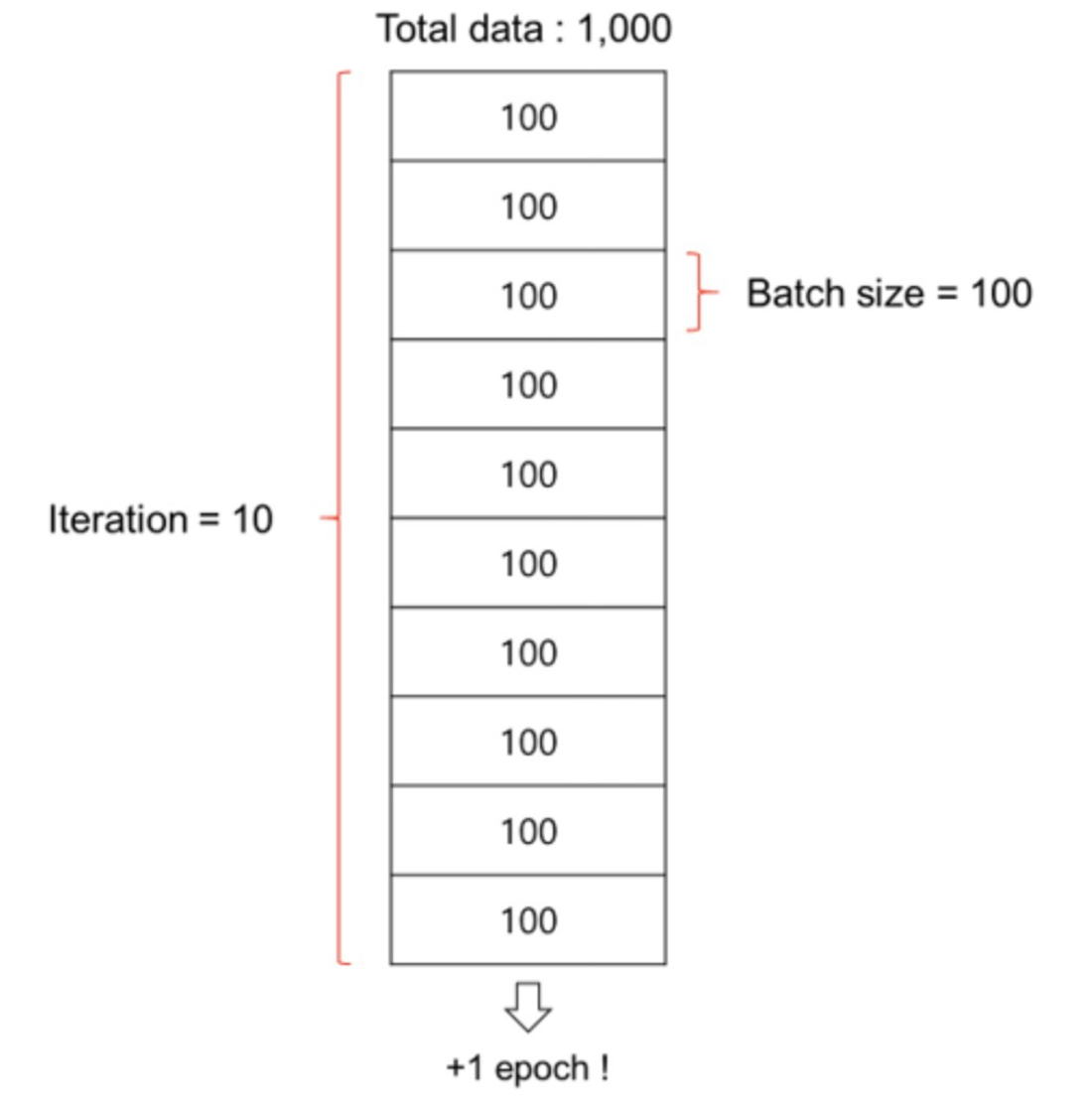
• batch(배치)와 iteration(이터레이션)
  만약 우리가 10,000,000개의 데이터셋을 가지고 있다고 가정합시다. 만약 우리가 10,000,000개의 데이터셋을 가지고 있다고 가정합시다. 10,000,000개의 데이터셋을 한꺼번에 메모리에 올리고 학습시키려면 엄청난 용량을 가진 메모리가 필요하고 그 메모리를 사는데 (메모리가 없다면 개발하는데) 천문학적인 비용이 들 것입니다. 따라서 우리는 이 데이터셋을 작은 단위로 쪼개서 학습을 시키는데 쪼개는 단위를 배치(Batch)라고 부릅니다. 예를 들어, 1,000만개의 데이터셋을 1,000개 씩으로 쪼개어 10,000번을 반복하는 것입니다. 이 반복하는 과정을 Iteration(이터레이션)이라고 부릅니다.

• epoch(에폭)
  이 과정은 우리가 수능시험을 대비해서 모의고사 문제를 여러 번 풀어보는 과정하고 비슷합니다. batch를 몇 개로 나눠놓았냐에 상관 없이 전체 데이터셋을 한 번 돌 때 한 epoch이 끝납니다.

=> 따라서 1천만개의 데이터셋을 1천개 단위의 배치로 쪼개면, 1만개의 배치가 되고, 이 1만개의 배치를 100에폭을 돈다고 하면 1만 * 100 = 100만번의 이터레이션을 도는 것이 됩니다.

2. Activation functions (활성화 함수)
   연구자들은 뉴런의 신호전달 체계를 흉내내는 함수를 수학적으로 만들었는데, 전기 신호의 임계치를 넘어야 다음 뉴런이 활성화 한다고해서 활성화 함수라고 부릅니다.

활성화 함수는 비선형 함수여야 합니다. 비선형 함수의 대표적인 예가 바로 시그모이드 함수입니다. 따라서 비선형 함수 자리에 시그모이드를 넣으면 아래와 같이 됩니다.

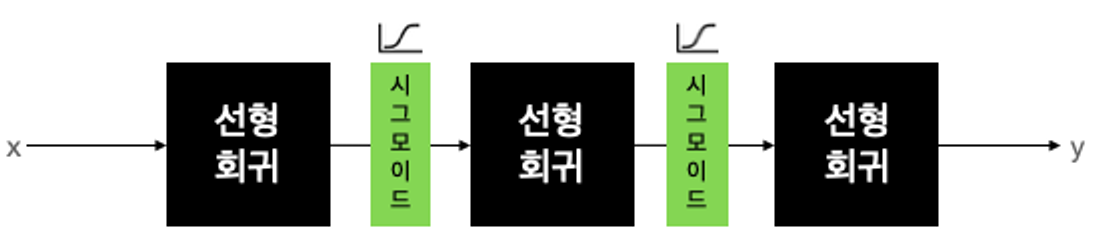
• 시그모이드 함수
  

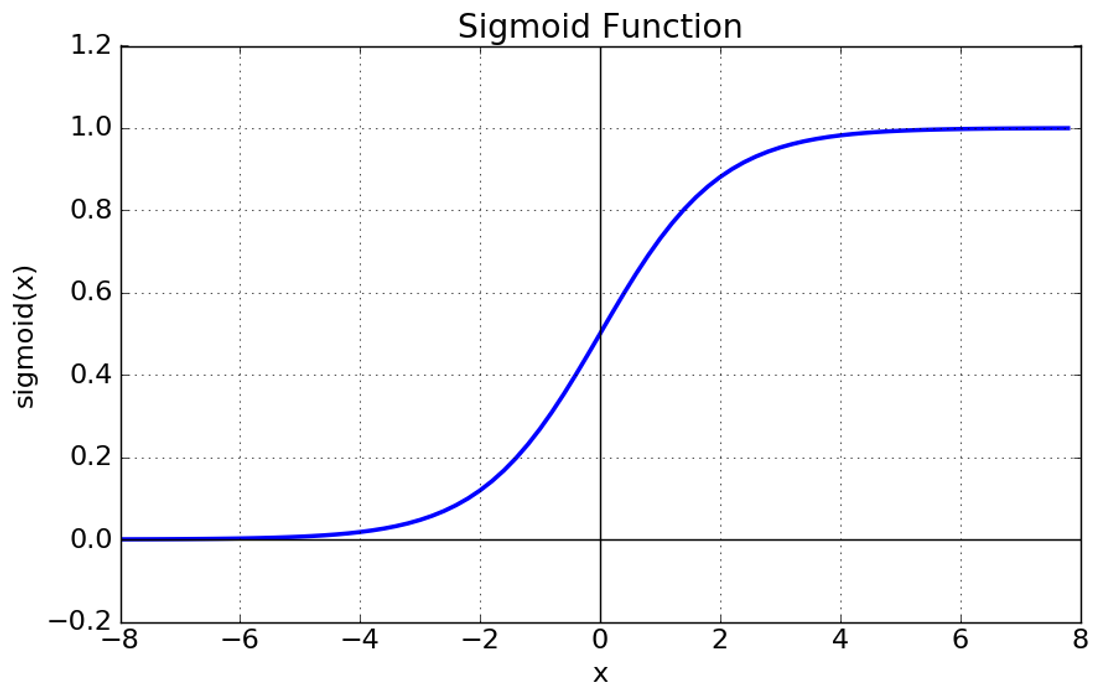
시그모이드 함수는 x가 -6보다 작을 때는 0에 가까운 값을 출력으로 내보내서 비활성 상태를 만듭니다. 반대로 x가 6보다 클때는 1에 가까운 값을 출력으로 내보내서 활성 상태로 만듭니다.

• 활성화 함수의 여러가지 종류
  
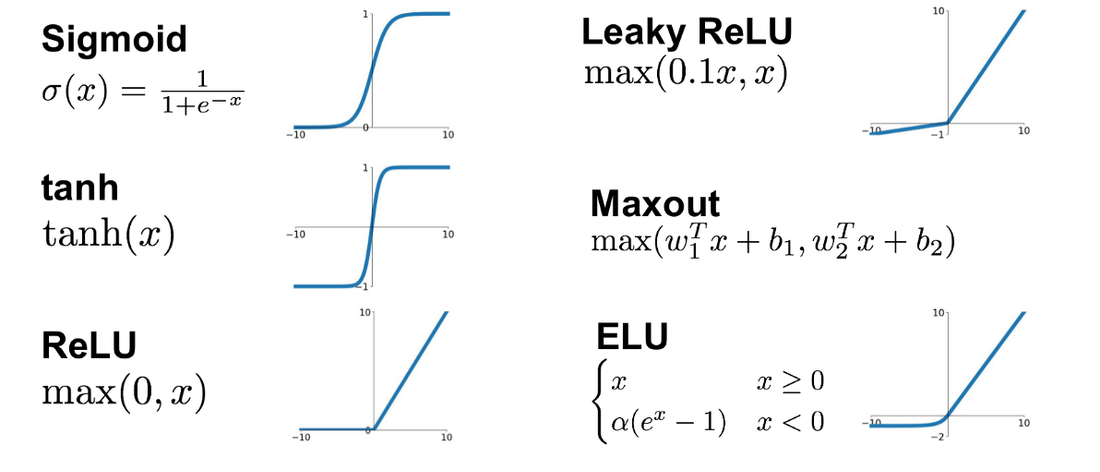
  딥러닝에서는 ReLU(렐루) 함수가 다른 활성화 함수에 비해 학습이 빠르고, 연산 비용이 적고, 구현이 간단하기 때문에 가장 보편적으로 쓰입니다. 대부분 딥러닝 모델을 설계할 때는 ReLU를 기본적으로 많이 쓰고, 여러 활성화 함수를 교체하는 노가다를 거쳐 최종적으로 정확도를 높이는 작업을 동반합니다. 이러한 노가다의 과정을 모델 튜닝이라고 부릅니다.

3. Overfitting, Underfitting (과적합, 과소적합)

딥러닝 모델을 설계/튜징하고 학습시키다 보면 가끔씩 Training loss는 점점 낮아지는데 Validation loss가 높아지는 시점이 있습니다. 이런 현상을 과적합 현상이라고 합니다.

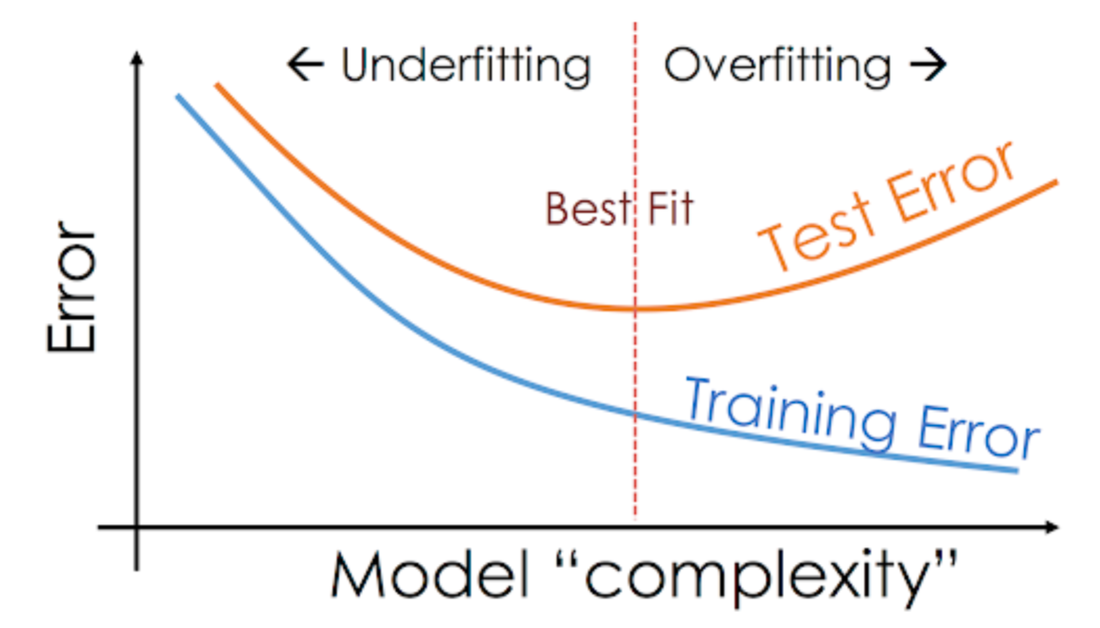
풀어야하는 문제의 난이도에 비해 모델의 복잡도(Complexity)가 클 경우 가장 많이 발생하는 현상입니다.

반대로 풀어야하는 문제의 난이도에 비해 모델의 복잡도가 낮을 경우 문제를 제대로 풀지 못하는 현상을 과소적합이라고 합니다.

따라서 우리는 적당한 복잡도를 가진 모델을 찾아야 하고 수십번의 튜닝 과정을 거쳐 최적합(Best fit)의 모델을 찾아야합니다.

딥러닝 모델을 학습시키다보면 보통 과소적합보다는 과적합때문에 골치를 썩는 경우가 많습니다. 과적합을 해결하는 방법에는 여러가지 방법이 있지만 대표적인 방법으로는 데이터를 더 모으기, Data augmenation, Dropout 등이 있습니다.

🐔 딥러닝의 주요 스킬

---

1. Data augmentation (데이터 증강기법)
   과적합을 해결할 가장 좋은 방법은 데이터의 개수를 늘리는 방법입니다. 하지만 실무에서는 데이터가 넘쳐나기는 커녕 부족한 경우가 매우 많습니다. 부족한 데이터를 보충하기위해 우리는 데이터 증강기법이라는 꼼수를 사용합니다. 데이터 증강기법은 이미지 처리 분야의 딥러닝에서 주로 사용하는 기법입니다.

원본 이미지 한 장을 여러가지 방법으로 복사를 합니다. 사람의 눈으로 보았을 때 위의 어떤 사진을 보아도 사자인 것처럼 딥러닝 모델도 똑같이 보도록 학습시킵니다. 이 방법을 통해 더욱 강건한 딥러닝 모델을 만들 수 있습니다.

=> 데이터 증강은 데이터를 인위적으로 확장하며, 학습 데이터의 다양성을 높이고 모델의 성능을 향상시킵니다.

2. Dropout (드랍아웃)

Dropout(드랍아웃)은 신경망 모델에서 과적합을 방지하기 위한 정규화 기법 중 하나입니다. Dropout은 단어에서도 의미를 유추할 수 있듯이 각 노드들이 이어진 선을 빼서 없애버린다는 의미가 있습니다. 신경망의 일부 뉴런을 임의로 비활성화시키는 방식으로 작동하며, 이를 통해 모델이 일반화 능력을 향상시키고 과적합을 감소시킵니다.

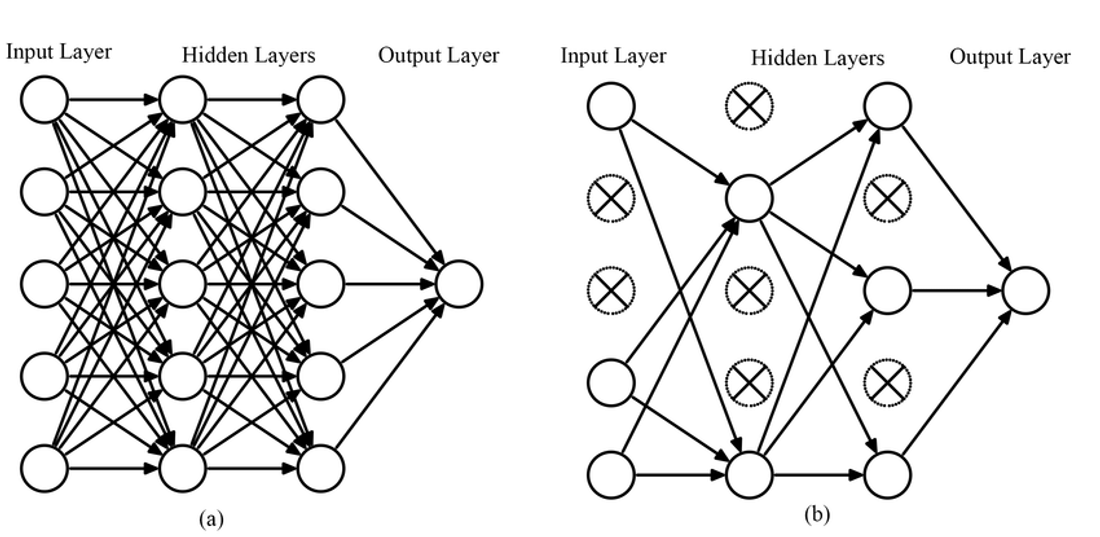
오른쪽 그림처럼 각 노드의 연결을 끊어버리는 작업을 하는데, 각 배치마다 랜덤한 노드를 끊어버립니다. 즉 다음 노드로 전달할 때 랜덤하게 출력을 0으로 만들어버리는 것과 같습니다.

"사공이 많으면 배가 산으로 간다"라는 속담처럼 과적합이 발생했을 때 적당한 노드들을 탈락시켜서 더 좋은 효과를 낼 수 있습니다.

예를 들어, 한 치과에 너무 많은 치과의사들이 있다고 가정해봅시다. 이들 중 일부만 있어도 충분히 치과는 돌아갈 것입니다. 이렇게 일부 의사들만 선출한다면 오히려 더 균형잡힌 운영이 가능성이 높습니다.

3. Ensemble (앙상블)
   Ensemble (앙상블)은 여러 모델을 각각 학습시킨 후 결합하여 단일 모델보다 우수한 예측 성능을 얻는 방법을 말합니다. 컴퓨팅 파워만 충분하다면 시도해볼만한 방법입니다. 여러 개의 모델에서 나온 예측을 결합하여 가장 많이 나온 클래스를 선택를 하는 방법도 있고, 평균 예측값을 구하는 방법도 있고, 마지막에 결정하는 레이어를 붙이는 경우 등 다양한 방법으로 응용이 가능합니다.

4. Learning rate decay (Learning rate schedules)
   Local minimum에 빠르게 도달하고 싶을 때 사용합니다. 학습률을 에보크마다 일정한 비율로 감소시킴으로써 모델이 더 정교하게 수렴하도록 돕습니다.

Keras에서는 tf.keras.callbacks.LearningRateScheduler() 와 tf.keras.callbacks.ReduceLROnPlateau() 를 사용하여 학습중 Learning rate를 조절합니다.

---

🥚🐣🐤🐥🐓🐔