[핸즈온 머신러닝] ch6. 결정트리

결정 트리 decision tree 는 랜덤 포레스트의 기본 구성 요소이고, 분류/ 회귀 / 다중 출력 작업까지 가능한 다목적 알고리즘이다.
따라서, 이번 장에서는 결정 트리의 훈련 , 시각화, 예측 방법, 규제, 제약 사항 등을 다루고자 한다.

1) 결정 트리 학습과 시각화

• 결정 트리 모델 DecisionTreeClassifier 훈련

  from sklearn.datasets import load_iris
  from sklearn.tree import DecisionTreeClassifier
  
  iris = load_iris(as_frame=True)
  X_iris = iris.data[["petal length (cm)", "petal width (cm)"]].values
  y_iris= iris.target
  
  tree_clf = DecisionTreeClassifier(max_depth=2, random_state=42)
  tre_clf.fit(X_iris, y_iris)

  • sklearn은 이진 트리만 만드는 CART 알고리즘을 사용함. 따라서, 분할 노드는 항상 두개의 자식 노드를 가짐
  • max_depth 조절을 통해 더 깊은 트리를 만들 수 있음

• 결정 트리 시각화
  1) export_graphviz() 를 통해 그래프 정의를 .dot 파일로 추출

  from sklearn.tree import export_graphviz
  
  export_graphviz(
  		tree_clf,
          	out_file="iris_tree.dot",
          	feature_names=["꽃잎 길이 (cm)", "꽃잎 너비 (cm)"],
            class_names=iris.target_names,
            rounded=True, # 박스의 모서리 둥글게 여부
            filled=True, # 노드의 색칠 여부
  		)

  2) graphviz.Source.from_file() 통해 시각화

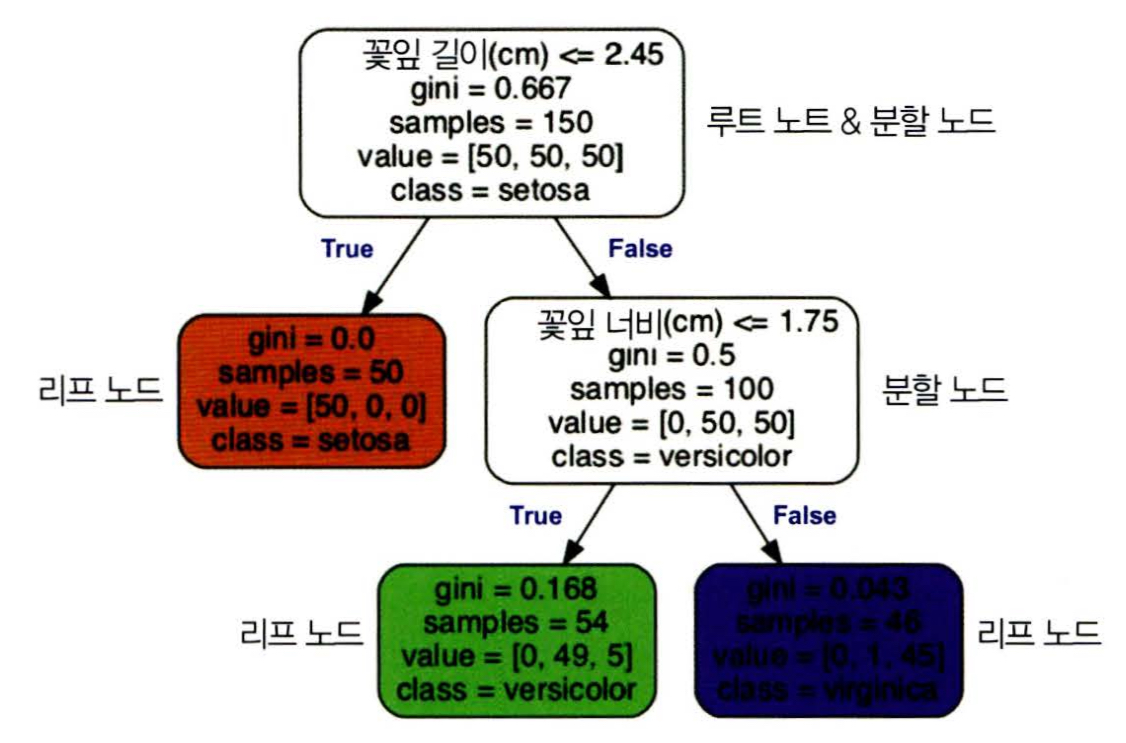
  • graphviz 는 오픈소스 그래프 시각화 소프트웨어 패키지로 .dot 파일을 pdf나 png 등과 같은 다양한 형식으로 변환하는 도구가 포함되어 있음

    from graphviz import Source
    
    Source.from_file("iris_tree.dot")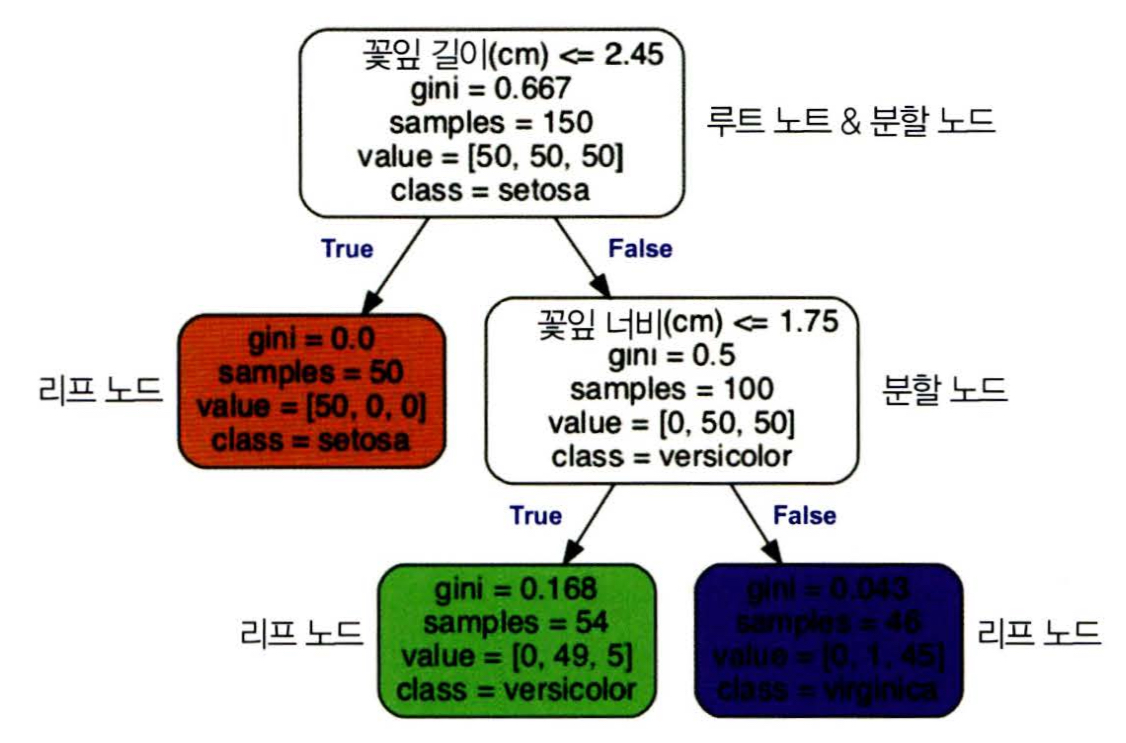

    

---

2) 예측

결정트리에서 예측 경로

• 루트 노드부터 조건에 부합하는지 여부를 확인하다가 리프노드( 더 이상 자식이 없는 노드 )를 만날 경우 최종 클래스를 예측
  
• 데이터 전처리( 특성의 스케일을 맞추거나, 평균을 원점에 맞추는 작업 )이 필요하지 않음

지니 불순도

$Gini = 1 - \sum_{k=1}^{K} p_k^2$

• 지니 불순도는 노드 안에 있는 샘플들의 클래스 혼합 정도를 나타내는 값
  • 따라서 모든 샘플이 같은 클래스에 속한다면 이 노드를 순수, 즉 gini=0

• 위에 시각화한 그림에서 초록색 노드를 예시로 들어서 설명해 보면,
  • samples = 54 : 54개의 샘플이 해당 노드에 해당
  • value=[0, 49, 5] : class 0으로 분류된 샘플이 0개, class 1로 분류된 샘플이 49개, class 2로 분류된 샘플이 5개
  • 해당 노드의 지니 불순도 = $1-{(0/54)}^2-{(49/54)}^2-{(5/54)}^2$

---

3) 클래스 확률 추정

• 결정 트리는 sample이 특성 클래스 k에 속할 확률 추정할 수 있음

>>> tree_clf.predict_proba[,15]]).round(3)
array([[0. , 0.907, 0.093]])
>>> tree_clf.predict([[5,1.5]])
array[1]

• predict_proba : 각 클래스의 속할 확률을 리스트로 return
• predict : 확률이 가장 높은 클래스를 return

---

4) CART 훈련 알고리즘

• 루트 노드에서 이진 ( True / False )로 구분하기 위해서는 1. 특성 k 와 2. 특성 k의 임계값을 설정해야함

• 가장 적합한 k와 임계값을 찾기 위한 CART 비용 함수
  

• 최대 깊이가 되거나, 불순도를 줄이는 조합을 찾을 수 없을 때 이 과정을 멈추게 됨

• CART는 현재 단계에서 즉시 가장 좋은 분할만 선택하기 때문에 탐욕 알고리즘임

탐욕 알고리즘 greedy algorithm

• 맨위 루트노드에서 최적의 분할을 찾고, 이어지는 단계에서 이 과정을 반복
• 몇 단계를 거치는 지에 대한 고려는 없음. 따라서 최적의 솔루션을 보장하지 않음
  • 최적의 트리 찾기 = NP-완전 문제

---

5) 계산 복잡도

훈련 알고리즘

• n개의 특성에 대해 m개의 노드를 비교하면 비교를 진행하게 되면 $O(n*m\log_{2} m)$

탐색 알고리즘

• 일반적인 결정 트리는 균형을 이루고 있기 때문에 $O(\log_{2} m)$

---

6) 결정 트리 평가

지니 불순도

• DecisionTreeClassifier 클래스는 기본적으로 지니 불순도 사용
• 가장 많이 차지하는 클래스가 누구냐에 집중 → 특정 클래스가 우세하면 그쪽으로 쉽게 치우침

엔트로피

• 전체 클래스 분포의 균형을 강조 → 작은 클래스까지 고려하여 분할

그렇다면 어떤 지표가 더 우세한 지표인가?

• 제곱 연산은 컴퓨터가 아주 빠르게 계산할 수 있지만, 로그 연산은 제곱보다 계산량이 많고 비용이 크기 때문에 지니 불순도가 일반적으로 계산이 조금 더 빠름
• 엔트로피를 사용하면, 소수 클래스까지 반영되어 트리가 조금 더 균형 잡히는 경향이 있음

---

7) 규제 매개변수

• 결정 트리는 훈련 데이터에 대한 제약사항( ex. 데이터가 선형 )이 거의 없기 때문에 과대적합되기 쉬움

• 결정트리는 훈련 전 파라미터 수가 결정되지 않으므로 비파라미터 모델 nonparametric model

  • 모델 구조가 데이터에 맞춰지므로 고정되지 않고 자유로움(과대적합될 가능성 높아짐)

  규제

• 과대 적합을 피하기 위해 결정 트리의 자유도를 제한 !

• scikit_learn에서는 max_depth 로 자유도를 제한

  • max_depth 를 줄이면 모델을 규제하고 과대적합의 위험을 감소시킴

• 추가 파라미터

   max_features : 각 노드에서 분할에 사용할 특성의 최대 수
    max_leaf_nodes : 리프 노드의 최대 수 
    min_samples_split : 분할되기 위해 노드가 가져야 하는 최소 샘플 수 
    min_samples_leaf : 리프 노드가 생성되기 위해 가지고 있어야할 최소 샘플 수 
    min_weight_fraction_leaf : 기능은 min_samples_leaf와 같지만, 가중치가 부여된 샘플 수에서의 비율을 고려
  

  • min_의 값을 증가시키거나, max_의 값을 감소시키면 규제 증가

• 예시

  from sklearn.datasets import make_moons
   X_moons, y_moons = make_moons(n_samples=150, noise=0.2, random_state=42)
     
   tree_clf1 = DecisionTreeClassifier(random_state=42)
   tree_clf2 = DecisionTreeClassifier(min_samples_leaf=5, random_stat=42)
   tree_clf1.fit(X_moons, y_moons)    	
   tree_clf2.fit(X_moons, y_moons)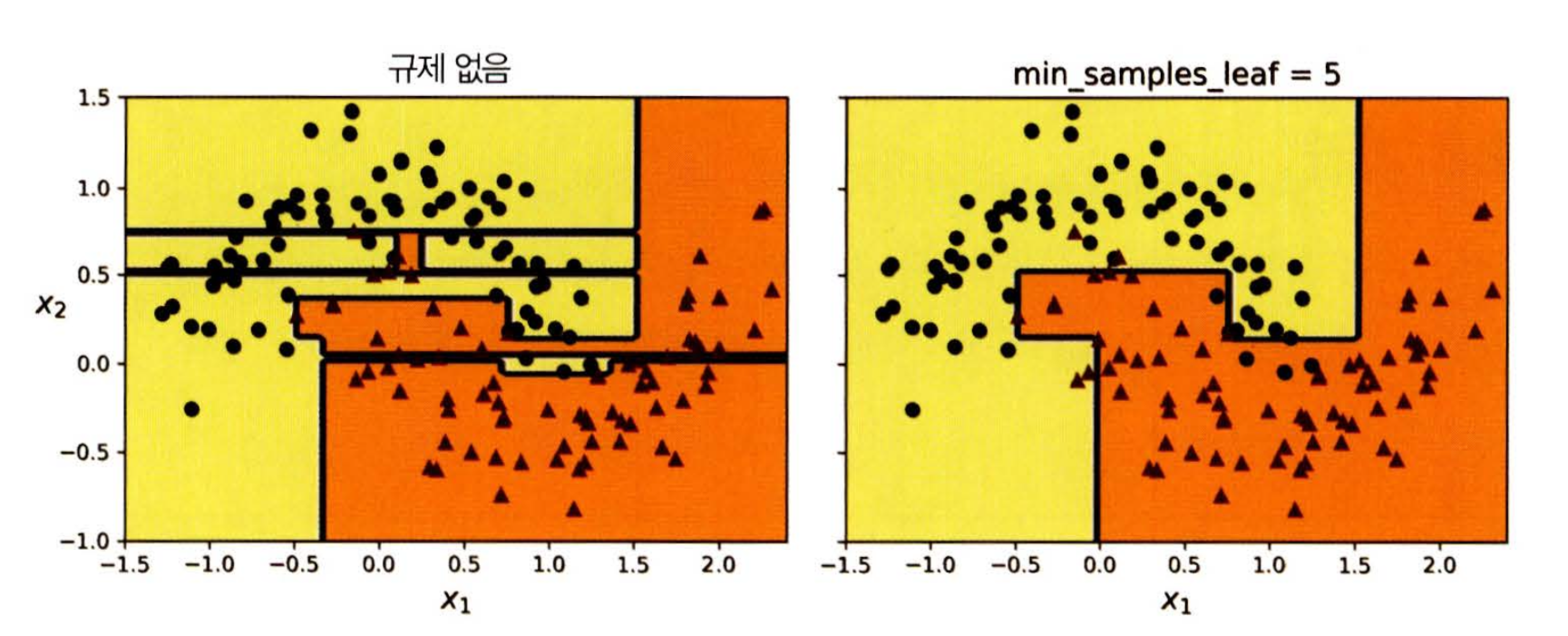

  

  X_moons_test, y_moons_test = make_moons(n_sampes=1000, noise=0.2, random_state=43)
  ....
  ...
  >>> tree_clf1.score(X_moons_test, y_moons_test)
  0.898
  >>> tree_clf2.score(X_moons_test, y_moons_test)
  0.92

  • clf1보다 clf2의 score가 더 높음 > 규제가 없는 것이 과대적합 확률이 더 높음

---

8) 회귀

• 결정 트리는 회귀 문제에서도 사용됨 DecisionTreeRegressor

import numpy as np
from sklearn.tree import DecisionTreeRegressor

np.random.seed(42)
X_quad = np.random.rand(200, 1) - 0.5 # 랜덤한 하나의 입력 특성
y_quad = X_quad ** 2 +0.025 * np.random.randn(200,1)

tree_reg = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg.fit(X_quad, y_quad)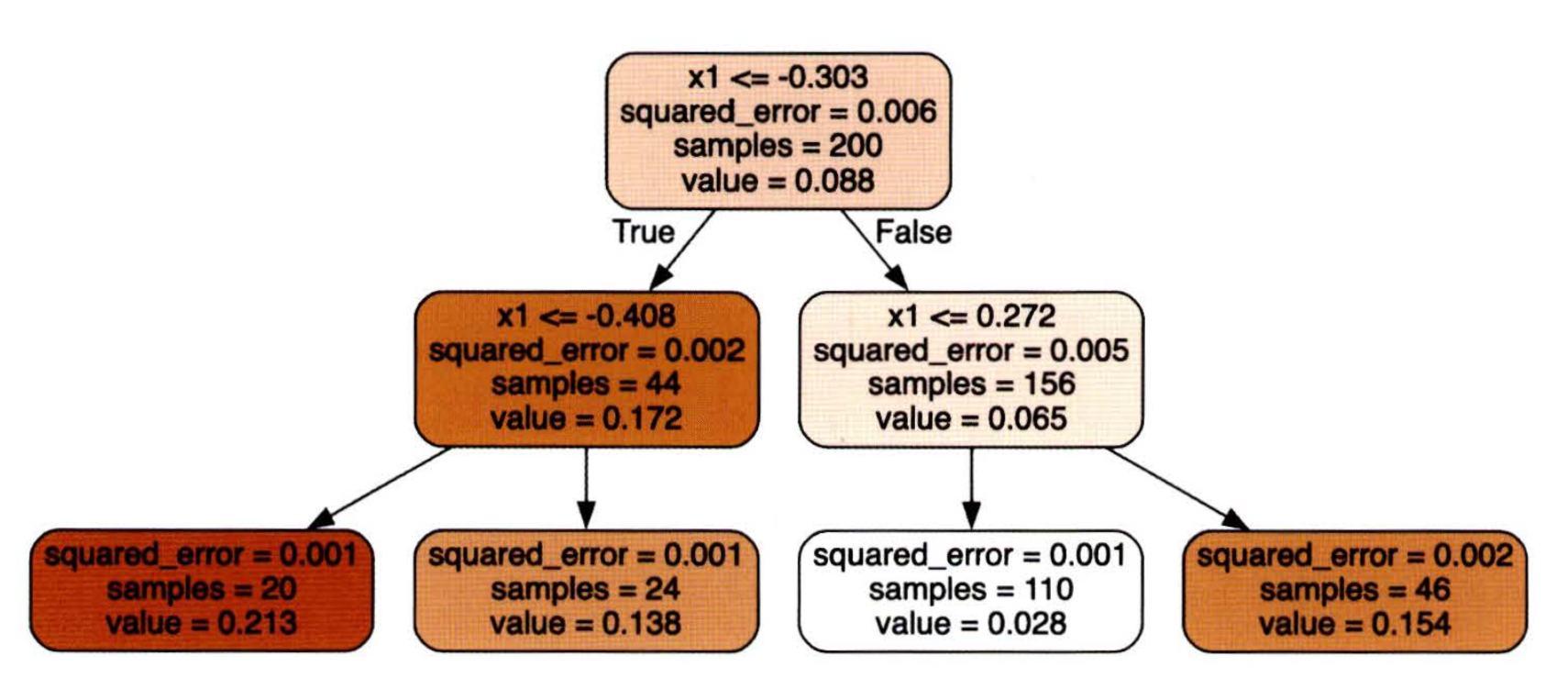

• 분류와 유사하지만, 특정 클래스를 예측하는 것 대신 어떤 값을 예측

회귀를 위한 CART 비용 함수

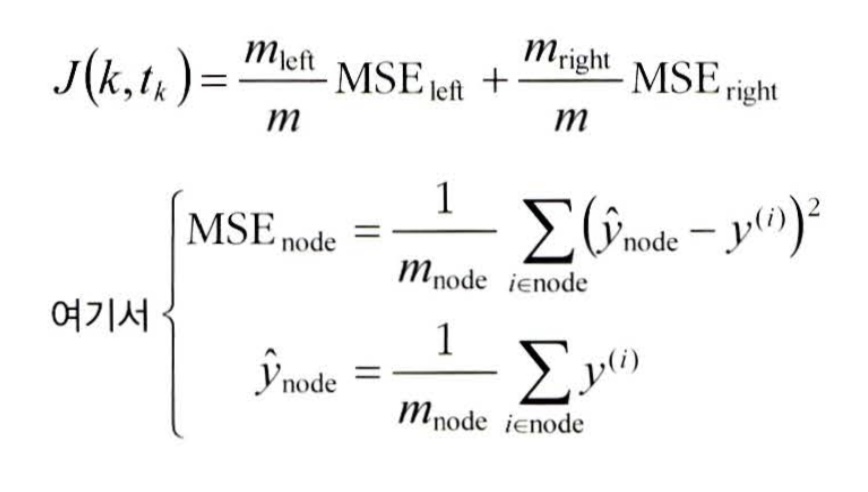
회귀 결정트리 과대적합

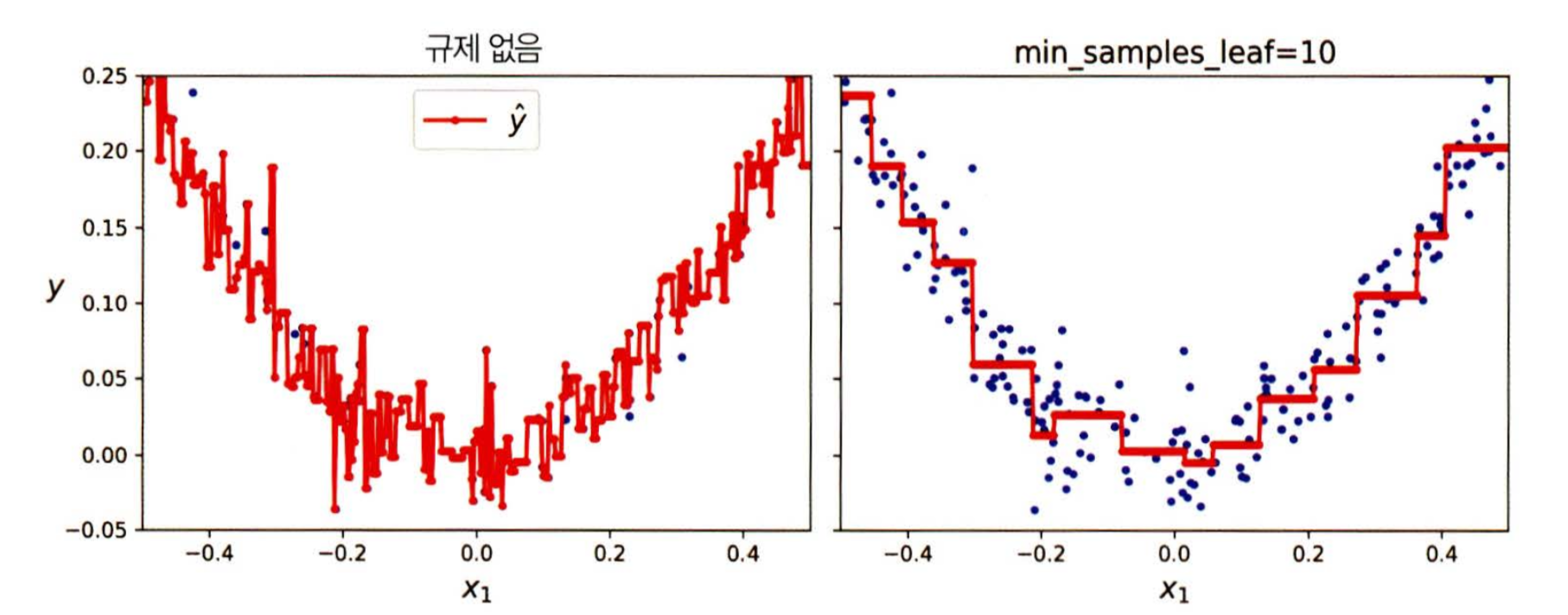
• 회귀 결정트리 역시 과대적합되기 쉬우므로 규제를 사용하는 것이 좋음

---

9) 축 방향에 대한 민감성

• 결정 트리는 계단 모양의 결정 경계를 생성하므로, 데이터의 방향에 민감

• 더 좋은 일반화를 위해서 PCA(주성분분석) 변환을 적용

  • 스케일 조정 & 데이터 회전

from sklearn.decomposition import PCA
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler

pca_pipeline = make_pipeline(StandardScaler(), PCA())
X_iris_rotated = pca_pipeline.fit_transform(X_iris)
tree_clf_pca = DecisionTreeClassifier(max_depth=2, random_state=42)
tree_clf_pca.fit(X_iris_rotated, y_iris)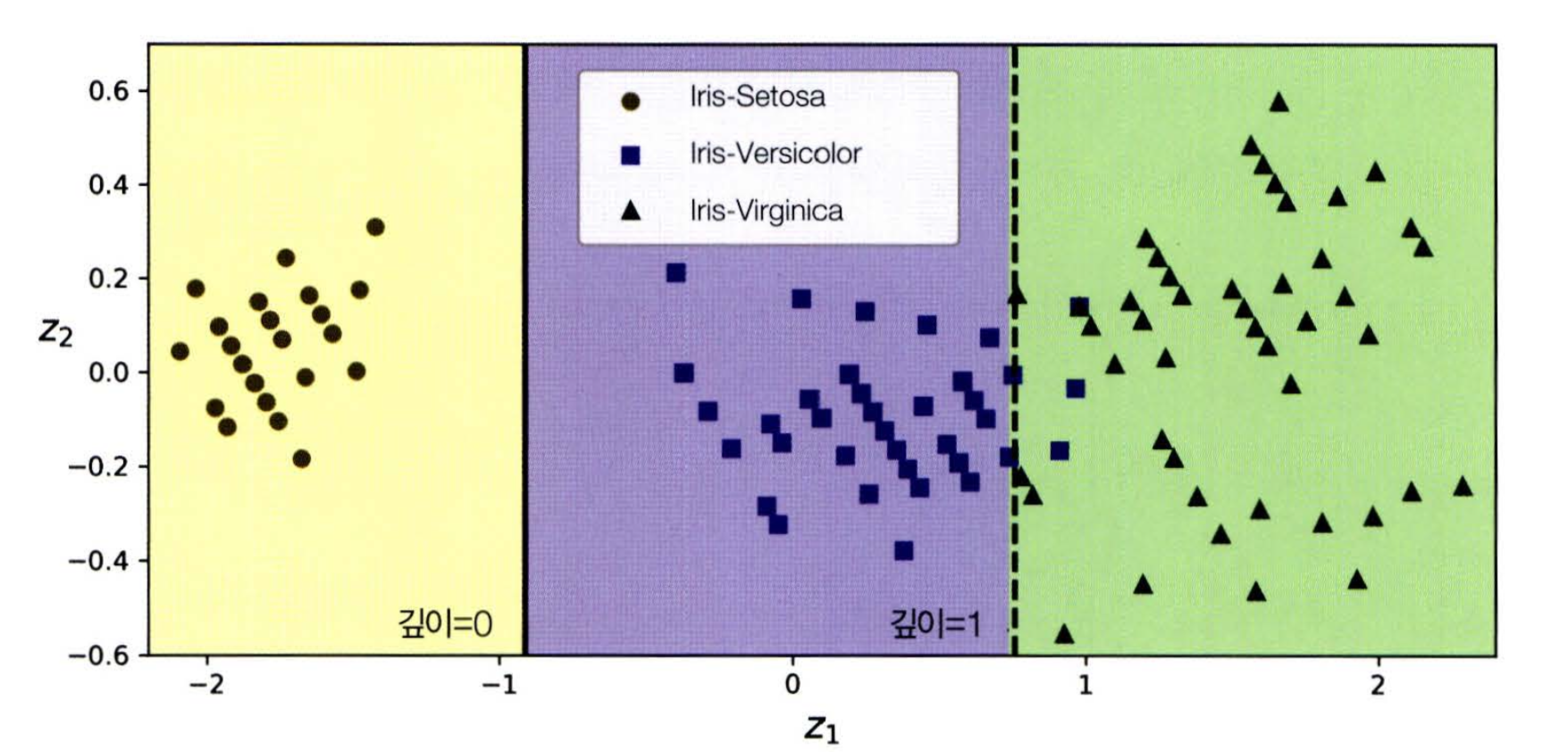

• PCA에 대해서는 8장에서 더 자세히 다룰 예정

---

10) 결정 트리의 분산 문제

• 결정 트리는 분산이 크다는 문제가 있음
  • 따라서 하이퍼파라미터, 데이터를 조금만 변경해도 전혀 다른 모델이 생성될 수 있음
  • random_state 매개변수 설정하지 않는 한 매우 다른 모델이 생성될 수도 있음
• 따라서, 여러 결정 트리의 예측의 평균(앙상블)을 사용하고, 이를 랜덤 포레스트라고 함
• 랜덤 포레스트에 대해서는 7장에서 더 자세히 다뤄볼 예정