[핸즈온 머신러닝] ch8. 차원축소

HOML (HandsOnMachineLearning)

목록 보기

7/7

대부분의 경우 머신러닝 문제는 훈련 샘플이 수천~수백만 개의 특성을 가지고 있다.
이러한 특성은 훈련을 느리게 할 뿐 아니라 좋은 솔루션을 찾기 어렵게 만든다.
이를 해결하기 위해 특성수를 크게 줄여서 문제를 해결하기도 한다. (차원축소)
오늘은 차원 축소에 사용되는 두가지 접근과, 차원 축소 기법에 대해 알아보도록 하겠다.

1) 차원의 저주

우리는 3차원 세계에 살고 있기 때문에 고차원 공간을 직관적으로 이해하기 어렵다. 또한, 고차원은 많은 공간을 가지고 있기 대문에 두 점이 같은 단위 초입방체에 놓여있더라도 멀리 떨어져 있을 수 있다. 따라서, 저차원일 때보다 예측이 더 불안정하다.

즉, 과대적합될 위험이 크다.

이론적으로, 차원의 저주를 해결하는 방법는 훈련 세트의 크기를 키운다. (현실적으로 불가능)

2) 차원 축소에 사용되는 접근법

2-1) 투영

실전의 문제는 훈련 샘플이 모든 차원에 걸쳐 균일하게 퍼져 있지 않다. 즉, 고차원 공간 안의 저차원 부분 공간에 대부분 놓여있다.

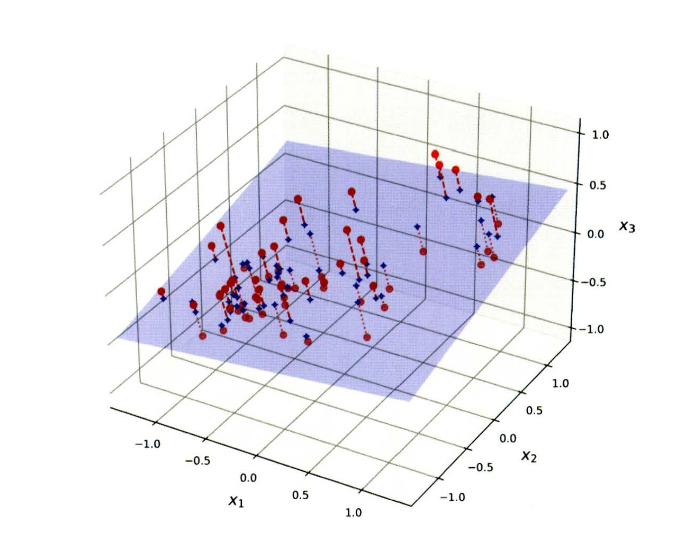
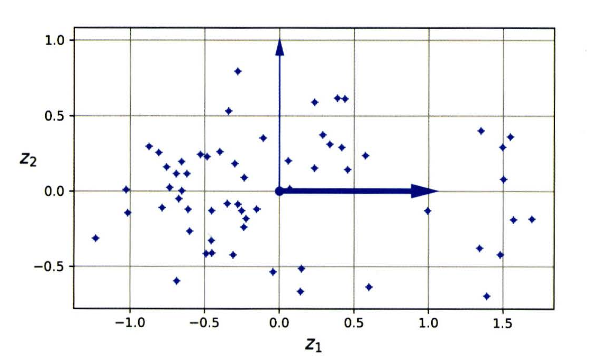
2차원에 가깝게 배치된 3차원 데이터셋

이 데이터셋은 거의 평면 형태로 놓여있다.
3D 공간에 있는 저차원(2D)로 볼 수 있다.

이를 투영하면 2D 데이터셋을 얻을 수 있다.

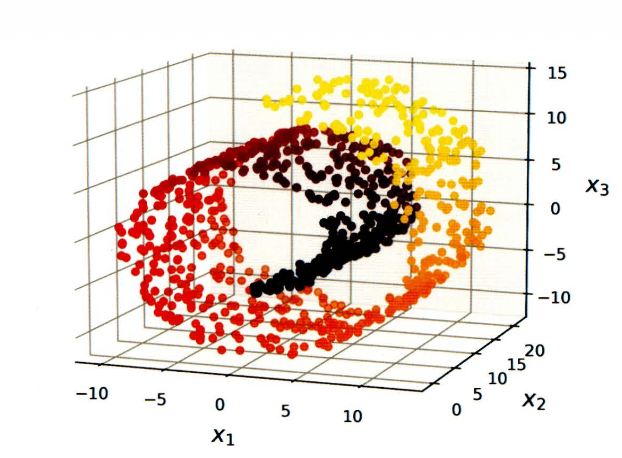
스위스롤 데이터셋

부분공간이 뒤틀리거나 휘어있는 데이터셋을 의미한다.

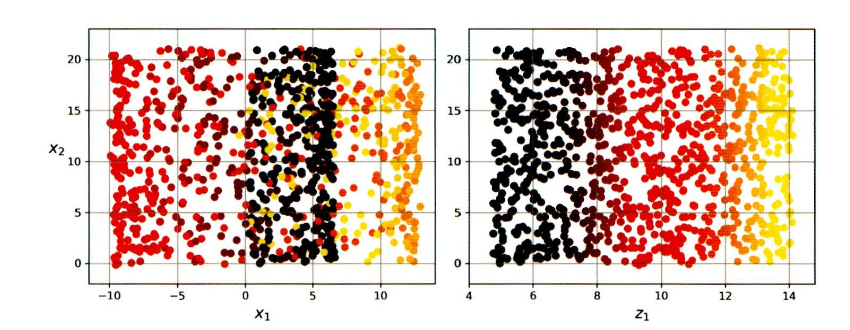
왼쪽) 투영결과, 오른쪽) 스위스 롤을 펼친 모습

이처럼 투영만으로는 원하는 결과를 얻기 어려울 때도 있다.

2-2) 매니폴드 학습

고차원 공간 속에 존재하지만 국소적으로는 d차원 평면처럼 보이는 구조

가정 : 실제 고차원 데이터는 더 낮은 차원의 매니폴드 위에 놓여 있다는 가정

학습

데이터가 있는 매니폴드를 학습해 차원을 줄이는 알고리즘
차원을 줄이면 훈련 속도가 향상된다.

하지만 이 원칙은 항상 성립하는 것은 아니다. 최종 성능은 데이터 구조에 따라 달라진다.

3) 주성분 분석 Principal component analysis (PCA)

가장 인기 있는 차원 축소 알고리즘으로, 데이터에 가장 가까운 초평면을 정의한 후에, 데이터를 이 평면에 투영 시킨다.

그렇다면 올바른 초평면을 고르는 것은 매우 중요한 일이다.

3-1) 분산 보존

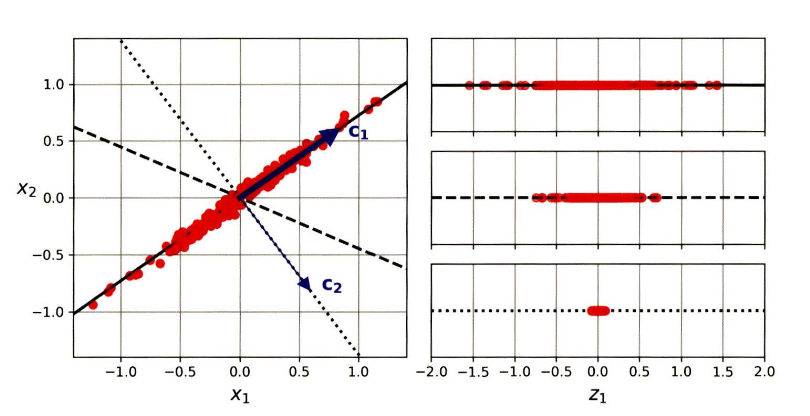
분산이 최대로 보존되는 축을 선택하는 것이 정보가 가장 적게 손실된다.
이는 원본 데이터셋과 투영된 것 가이의 평균 제곱 거리를 최소화하는 축이다.

3-2) 주성분

따라서, PCA는 훈련세트에서 분산이 최대인 축을 찾는다.
그리고, 첫번째 축에 직교하면서 남은 분산을 최대한 보존하는 두번째 축을 찾고, 이를 계속 반복하면서 n번째 축을 찾는다.

주성분을 찾을 때는 특잇값 분해라는 분해 기술을 활용한다.

import numpy as np

x= [...] # 3D 데이터셋이라고 가정
X_centered = X - X.mean(axis=0)
U, s, Vt= np.linalg.svd(X_centered)
c1 = Vt[0]
c2 = Vt[1]

pca 모델을 사용해 데이터셋의 차원을 줄이는 코드

from sklearn.decomposition import PCA
pca = PCA(n_components=2)
X2D = pca.fit_transform(X)

설명된 분산의 비율

      » pca.explained_variance_ratio_
      array([0.7578477, 0.15186921])

데이터셋의 분산의 76%가 첫번째 축을 따라 놓여 있고, 15%는 두번째 축을 따라 놓여 있음을 의미한다.
따라서, 세번째 축에는 9% 미만 (즉, 아주 적은 양의 정보)가 들어있을 것이다.

적절한 차원 선택

축소할 차원을 임의로 정하기보다 충분한 분산이 될 때까지 더해야 할 차원수를 선택한다.

from sklearn.datasets import fetch_openml


mnist = fetch_openml('mnist_784', as_frame=False)
X_train, y_train = mnist.data[:60_000], mnist.target[:60_000]
X_test, y_test = mnist.data[60_000:], mnist.target[60_000:]

pca = PCA()
pca.fit(X_train)
cumsum = np.cumsum(pca.explained_variance_ration_)
d = np.argmax(cumsum >= 0.95) + 1 # 차원

# 보존하려는 비율로 n_components를 설정
pca = PCA (n_components=0.95)
X_reduced = pca.fit_transform(X_train)

pca.n_components_ # 훈련 중 주성분 개수는 이 속성에 저장

3-3) 압축을 위한 PCA

압축된 데이터셋에 PCA 투영의 변환을 반대로 적용해서 다시 고차원으로 되돌릴 수도 있다.
하지만, 일정량의 정보는 잃어버렸기 때문에 완전히 복원시키는 어렵다.

X_recovered = pca.inverse_transform(X_reduced)

왼쪽) 원본, 오른쪽) 압축 후 복원

3-4) 다양한 PCA

랜덤 pca

확률적 알고리즘을 사용해 d개의 주성분에 대한 근사값을 찾음
$O(m \times d^2) + O(d^3)$ 의 계산 복잡도

rnd_pca = PCA(n_components=154, svd_solver= ”randomized", random_state=42)
X_reduced = rnd_pca.fit_transfonn(X_train)

점진적 pca

PCA 구현의 문제는 SVD 알고리즘을 실행하기 위해 전체 훈련 세트를 메모리에 올려야 한다는 것이다.
점진적 PCA(IPCA)는 훈련 세트를 미니 배치로 나눈 뒤 IPCA 알고리즘에 한 번에 하나씩 주입한다.


from sklearn.decomposition import IncrementalPCA

n batches = 100
inc_pca = IncrementalPCA(n_components=154)
for X_batch in np.array_split(X_train, n_batches):
  inc_pca.partial_fit( X_batch )
X_reduced = inc_pca.transform(X_train)

filename = ”my_mnist.mmap ”
X_mmap = np.memmap (filename, dtype='float32’, mode='write’, shape=X_train.shape) 
X_mmap[:] = X_train # 대신 반복을 사용해 데이터를 한 정 크씩 저장할 수 있습니다 .
X_mmap.flush ()

memmap 파일을 로드하고 일반적인 넘파이 배열처럼 사용할 수 있다.

X_mmap = n.memmap (filename, dtype='float32', mode='readonly').reshape(-1,784)
batch_size=X_mmap.shape[0] // n_batches
inc_pca = IncrementalPCA(n_components=154, batch_size=batch_size)
inc_pca .fit (X_mmap)

4) 랜덤 투영

랜덤한 선형 투영을 사용해 데이터를 저차원 공간에 투영한다.
이는, 윌리엄 B.존슨, 요람 린덴스트라우스에 의해 수학적으로 증명되어 있다.
랜덤 투영은 고차원 데이터에는 적합하지만, 저차원 데이터에 대해서는 잘 작동하지 않는다.

랜덤한 투영은 실제로 거리를 상당히 잘 보존할 가능성이 매우 높고, 따라서 투영 후에도 비슷한 두개의 샘플은 비슷한 채로 남고 매우 다른 두개의 샘플은 매우 다른 채로 남는다.

허용 오차 이상으로 변하지 않도록 보장하기 위한 최소 차원 수를 결정하는 방정식을 생각해 냈다.
johnson_lindenstrauss_min_dim()에 구현되어 있다.

from sklearn.random_projection import johnson_lindenstrauss_min_dim
m, ε = 5_000, 0.1
d = johnson_lindenstrauss_min_dim(m, eps=ε)
>>> d
7300

각 항목을 평균 , 분산 $1/d$ 의 가우스 분포에서 랜덤 샘플링한 [d,n] 크기의 랜덤 행렬 P를 생성하고 이를 사용하여 데이터셋을 n → d차원으로 투영할 수 있다.

n = 20_000
np.random.seed(42)
P = np.random.randn(d,n) / np.sqrt(d) # 표준편차

X = np.random.randn(m, n)
X_reduced = X @ P.T

사이킷런은 두 번째 랜덤 투영 변환기도 제공한다.

5) 지역 선형 임베딩

지역 선형 임베딩 locally linear embedding(LLE)은 비선형 차원 축소 기술이다.
투영에 의존하지 않는 매니폴드 학습이다.
LLE는 먼저 각 훈련 샘플이 최근 접 이웃에 얼마나 선형적으로 연관되어 있는지 측정하고, 국부적인(어느 한 부분에만 한정되는) 관계가 가장 잘 보존되는 훈련 세트의 저차원 표현을 찾는다.

스위스 롤을 만들고 LocallyLinearEmbedding을 사용해 펼쳐본다.

from sklearn.datasets import make_swiss_roll
from skleanr.manifold import LocallyLinearEmbedding

X_swiss, t = make_swiss_roll(n_samples=1000, noise=0.2, random_state=42)
llle = LocallyLinearEmbedding(n_components=2, n_neighbors=10, random_state=42)
X_unrolled = lle.fit_transform(X_swiss)

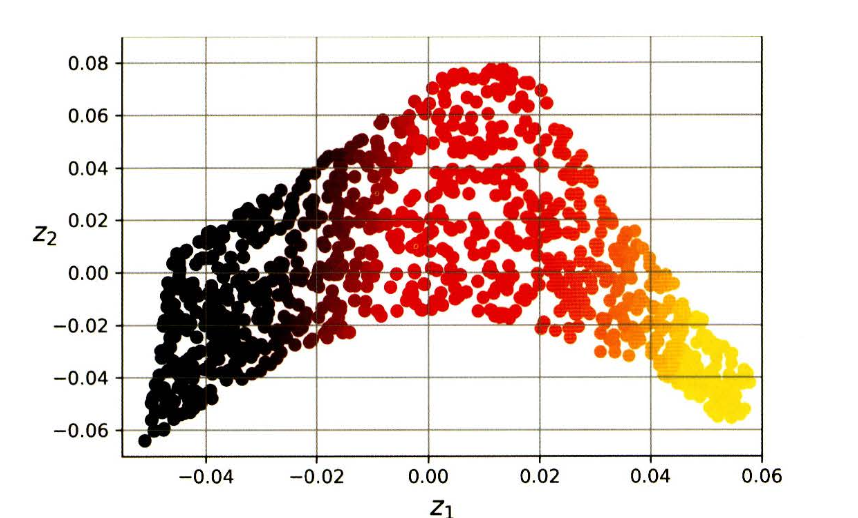
LLE를 사용해 펼친 스위스롤

LLE 작동 방식

알고리즘이 각 훈련 샘플(X)에 대해 K개의 최근접 이웃을 찾는다.
이 이웃에 대한 선형 함수로 X를 재구성한다.
- $x^i$ 와 $∑_{j=1}^m w_{i,j} x^j$ 사이의 제곱 거리가 최소가 되는 $w_{i,j}$ 를 찾는 것이다.
- 여기서 $x^j$ 가 $x^i$ 의 가장 가까운 k개 이웃 중 하나가 아닐 경우에는 $w_{i,j} = 0$ 이 된다.
가중치 행렬 W는 훈련 샘플 사이에 있는 지역 선형 관계를 담고 있다.
- 여기서는 가능한 이 관계가 보존되도록 훈련 샘플을 d차원으로 매핑한다.

2,3 단계는 비슷해 보이지만 2단계는 샘플을 고정하고 최적의 가중치를 찾는 과정이고, 3단계는 저차원 공간에서 샘플 이미지의 최적의 위치를 찾는다.
scikitlearn에서 제공하는 LLE 구현의 계산복잡도는
1. 이웃 탐색: $( O(m \log m + n \log k))$
2. 가중치 최적화: $( O(m n k^5) )$
3. 저차원 표현 생성: $( O(d m^2))$

6) 추가적인 차원 축소 기법

6-1) 다차원 스케일링 multidimensional scaling(MDS)

샘플 간의 거리를 보존하면서 차원을 축소한다.

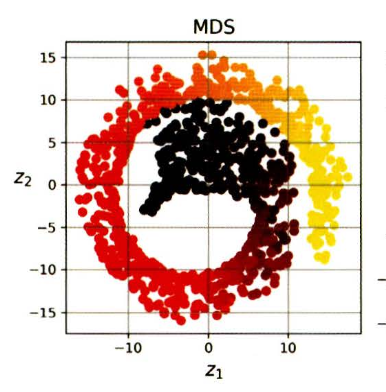
MDS를 활용해 스위스롤을 2D로 축소

6-2) Isomap

각 샘플을 가장 가까운 이웃과 연결하는 식의 그래프를 만들고, 샘플 간 지오데식 거리를 유지하면서 차원을 축소한다.
두 노드 사이의 지오데식 거리는 두노드 사이의 최단 경로를 이루는 노드의 수이다.
스위스롤의 곡률을 완전히 없앤다. (클러스터를 강조하기 위해 롤을 분해한다.)

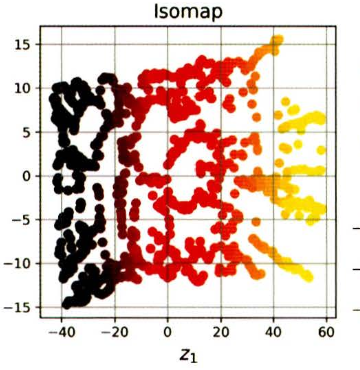
Isomap를 활용해 스위스롤을 2D로 축소

6-3) t-SNE

비슷한 샘플은 가까이, 비슷하지 않은 샘플은 멀리 떨어지도록 하면서 차원을 축소한다.
시각화에 많이 사용되고, 특히 고차원 공간에 있는 샘플의 군집을 시각화할 떄 많이 사용된다.

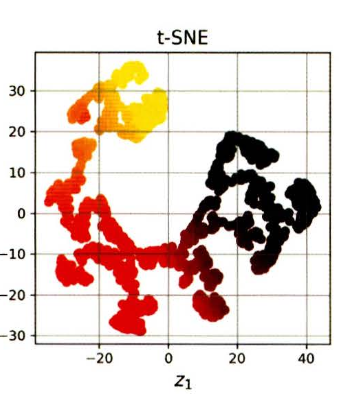
t-SNE 활용해 스위스롤을 2D로 축소

6-4) 선형 판별 분석 (LDA)

선형 분류 알고리즘으로, 훈련 과정에서 클래스 사이를 가장 잘 구분하는 축을 학습한다.
그리고 이 축을 데이터가 투영되는 초평면을 정의하는데 사용한다.
이 알고리즘은 투영을 통해 가능한 한 클래스를 멀리 덜어지게 유지시키므로, 다른 알고리즘을 적용하기 전에 차원 축소하기 용이함.

인공지능세포

이전 포스트