1. 개요
원본 문제 링크: https://www.acmicpc.net/problem/6549
문제 접근법: 분할정복, 그리디 알고리즘
2. 코드
# parameters are index of input array
def solve(start, end):
global input_arr
left_idx = start
mid_idx = (start + end) // 2
right_idx = end
#print('left_idx: {}, right_idx: {}'.format(left_idx, right_idx))
if start == end:
#print('returned: {}'.format(input_arr[start]))
return input_arr[start]
area = max(solve(start, mid_idx), solve(mid_idx + 1, end)) # to be determined
#if left_idx == 0 and right_idx == len(input_arr)-1:
# print('this is root case')
left_idx = right_idx = mid_idx
minH = input_arr[mid_idx]
lborder_flag = False
rborder_flag = False
# There's only one idx displacement per loop
while lborder_flag == False or rborder_flag == False:
if left_idx == start:
lborder_flag = True
if right_idx == end:
rborder_flag = True
# case 1 : if mid_idx is surrounded with higher heights -> proceed both idx's
if lborder_flag == False:
if input_arr[left_idx - 1] >= input_arr[left_idx]:
left_idx -= 1
area = max(area, minH * (right_idx - left_idx + 1))
continue
elif rborder_flag == False:
if input_arr[right_idx + 1] >= input_arr[right_idx]:
right_idx += 1
area = max(area, minH * (right_idx - left_idx + 1))
continue
# case 2 : if mid_idx is surrounded with lower heights
# -> compare left_idx and right_idx and proceed the higher idx
if lborder_flag == True and rborder_flag == False:
right_idx += 1
minH = min(minH, input_arr[right_idx])
area = max(area, (right_idx - left_idx + 1) * minH)
continue
elif lborder_flag == False and rborder_flag == True:
left_idx -= 1
minH = min(minH, input_arr[left_idx])
area = max(area, (right_idx - left_idx + 1) * minH)
continue
elif lborder_flag == False and rborder_flag == False:
if input_arr[left_idx - 1] <= input_arr[right_idx + 1]:
right_idx += 1
minH = min(minH, input_arr[right_idx])
area = max(area, (right_idx - left_idx + 1) * minH)
continue
elif input_arr[left_idx - 1] >= input_arr[right_idx + 1]:
left_idx -= 1
minH = min(minH, input_arr[left_idx])
area = max(area, (right_idx - left_idx + 1) * minH)
continue
#print('returned: {}'.format(area))
return area
input_arr = []
while True:
arr = list(map(int, input().split()))
input_arr = arr[1:]
if arr[0] == 0:
break
ans = solve(0, len(input_arr)-1)
print(ans)3. 풀이 메모
언뜻보면 부분 문제 풀이가 전체 문제풀이로 귀결되지 않는 것처럼 보여 분할 정복이 가능한지는 확신이 잘 안 선다. 일단 분할 정복이 가능하다고 가정하고, 입력을 반으로 나눴을 때 직사각형의 최대 넓이가 나오는 유형은 다음 중 하나라고 볼 수 있다.
- 왼쪽 구역에서의 직사각형의 최대 넓이
- 오른쪽 구역에서의 직사각형의 최대 넓이
- 중간 경계에 걸쳐있는 직사각형의 최대 넓이
만약 3번째 경우만 어떻게든 해결한다면 분할 정복이 적용 가능할 것이다. 각 구역의 중간 지점을 정하고, 좌우 방향으로 2개의 포인터를 선언하고 그 포인터가 가리키는 지점을 중앙으로부터 점점 넓혀 나가며 최대 넓이를 갱신하면 된다. (앞으로 이 글에서는 동일한 논리를 적용할 때는 '중앙 그리디 알고리즘' 이라 표기한다)
이 넓혀나가는 기준은 그리디 알고리즘을 따를 수 있다. 이러한 근거는 다음과 같다.
- 탐욕적 선택 속성(Greedy Choice Property)
중앙에서 좌우 포인트를 넓혀 나간다 하더라도 막대들의 높이는 변하지 않을 뿐더러, 이전에 긴 막대를 골랐다고 바로 다음에는 반드시 어떤 특정한 길이의 막대를 골라야만 한다던가 하는 규칙도 없다. 따라서 현재의 선택이 이후의 선택에 영향을 주지 않게 된다.- 최적 부분 구조(Optimal Substructure)
중앙에서 포인터를 좌우로 넓혀 가는 하나 하나의 step은 독립적이다. 좌우 포인터의 이동은 '보이는 시야의 넓힘'으로 비유할 수 있다.
이처럼 초기 상태에서 시야를 한칸씩 넓혀간다고 볼 수 있다. 현재 step에서 보이는 최대 넓이를 고려하며 탐욕스럽게 좌우 포인터를 끝까지 진행한다면, 최종적으로는 '중앙에서 시작했을 때 최대 넓이' 라는 문제에 한해서는 정답에 도달할 수 있게 된다.
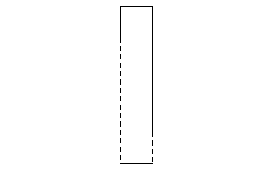
정말 이걸로 충분할까? 다음과 같이 운 나쁘게 중앙 포인터가 다음과 같이 지정된다면 그냥 망하는거 아닐까?
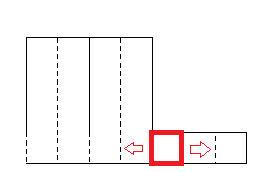
당연히 이 경우는 너비가 7인 납작한 사각형의 넓이를 최대라고 판단할 것이다. 여기서 그리디 알고리즘의 도입은 실패라고 생각할 수 있다. 그리고 언뜻 보면, 모든 입력 요소에 대해서 중앙 그리디 알고리즘을 적용해야만 비로소 최종 정답에 도달할 수 있는 것처럼 보인다.
하지만 여기서 분할정복과 그리디 알고리즘의 기묘한 케미가 발휘된다. 혹시 하나하나 모든 요소에 적용하는게 아니라, 분할된 각 구역마다 중앙 그리디 알고리즘을 적용하는 것만으로도 충분하지 않을까? 확신이 없으니 일단 각각의 경우를 따져가며 상황이 어떻게 변해가는지 관찰해보자.
1. 구역 내 요소가 1개인 경우
자기 자신을 최대 넓이값으로 리턴한다.
2. 구역 내 요소가 2개인 경우
결과인 최대 넓이는 너비1인 직사각형 넓이거나, 너비2인 직사각형 넓이거나 둘 중 하나밖에 없다. 여기서 중앙 그리디 알고리즘을 적용하면 모든 경우의 수에 대해서 고려해줄 수 있다. (중앙은 둘 중 하나가 되며, 좌우 인덱스는 딱 한칸만 진행하고 끝이 날 것이다)
3. 구역 내 요소가 3개인 경우
구역 내 요소가 2개인 경우와 1개인 경우로 분할이 된다. 각 분할 구역에서의 최대 넓이를 받아서 '왼쪽 구역 최대 넓이' / '오른쪽 구역 최대 넓이' 로 별도의 변수에 저장하고, 중앙에서 그리디 알고리즘을 적용해 '중앙 최대 넓이' 를 별도의 변수에 저장한다. 이렇게 계산된 3개의 값을 모두 취합해 최대값을 구해 리턴하면, 구역 내 요소가 3개인 경우에 대한 최대 넓이를 고려하는 작업이 끝난다.
area = max(왼쪽 구역 최대 넓이, 오른쪽 구역 최대 넓이, 중앙 최대 넓이) return area4. 구역 내 요소가 4개인 경우
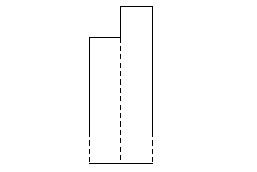
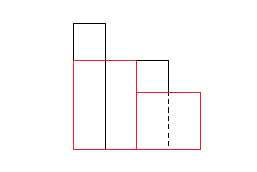
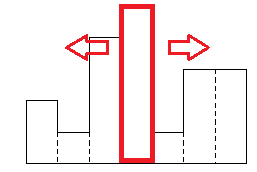
구역 내 요소가 2개인 경우와 2개인 경우로 분할이 된다. 아래 그림에서 중앙을 두번째 막대라고 가정하고 논의를 시작해보자.
(스케일은 무시하자. 정 거슬린다면 붉은색 직사각형들의 넓이는 4보다 크다고 가정하자)
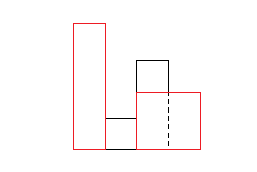
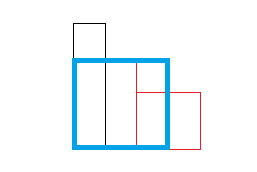
붉은색으로 강조된 직사각형은 각 분할 구역(좌우로 2칸씩 나눔)에서 얻어낸 최대 넓이에 해당하는 직사각형들이다. 여기선 중앙 그리디 알고리즘을 적용해서 중앙(두번째 막대)에서 인덱스를 이동시켜가며 최대 넓이값을 얻어도, 왼쪽 구역과 오른쪽 구역에서 얻은 최대 넓이 직사각형보다는 작다. 따라서 위 그림에서의 최대 넓이는 그대로 왼쪽 구역, 혹은 오른쪽 구역에서의 최대 넓이 직사각형이 될 것이다.area = max(왼쪽 구역 최대 넓이, 오른쪽 구역 최대 넓이, 중앙 최대 넓이) return area # area는 왼쪽 구역 최대 넓이 혹은 오른쪽 구역 최대 넓이가 나옴다음의 경우는 어떨까?
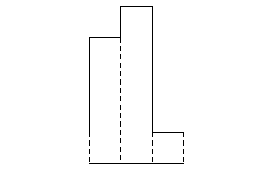
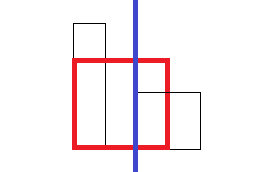
바로 위 그림에서 두번째 막대의 길이만 바꿨다. 중앙 그리디 알고리즘을 두번째 막대에서 적용하면, 다음을 최대 넓이라고 계산할 것이다.
이전과는 다르게, 왼쪽 구역과 오른쪽 구역을 동시에 침범하며 직사각형의 넓이가 계산된다. 따라서 최대 넓이는 중앙 최대 넓이로 갱신된다.area = max(왼쪽 구역 최대 넓이, 오른쪽 구역 최대 넓이, 중앙 최대 넓이) return area # area는 중앙 최대 넓이가 된다.
대충 정리가 되었다고 본다. 중앙 지점에서 출발한 좌우 포인터는 무엇을 최대 직사각형으로 잡을 지는 다음 두 경우밖에 없다.
1) 두 구역을 걸쳐있는 직사각형
2) 한 구역에만 걸쳐있는 직사각형
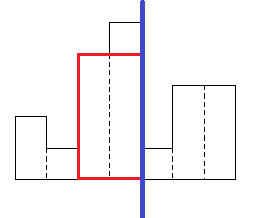
하지만 한 구역에만 걸쳐있는 직사각형의 최대 넓이는 이미 분할 정복을 통해서 고려된 값이다. 다시 말해, 다음과 같은 오른쪽에 엄청 큰 직사각형이 '숨어 있는' 경우는 이미 고려가 됐으니 걱정을 안해도 된다는 뜻이다.
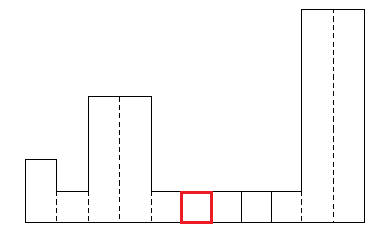
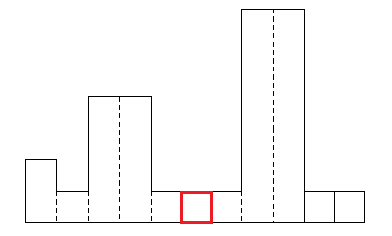
각 분할 구역에서 최대 직사각형 넓이를 내놓을 것이고, 그 과정에서 오른쪽 큰 직사각형 넓이는 여전히 최상위 트리 노드에 갈 때까지 '오른쪽 5칸을 대표하는 최대값' 으로 남겨져 올라오게 될 것이다.
area = max(왼쪽 구역 최대 넓이, 오른쪽 구역 최대 넓이, 중앙 최대 넓이)
return area각 분할 구역에 대해서 그리디 알고리즘을 적용한다면 logN 회 그리디 알고리즘이 실행되며, 그 실행 과정에서 모든 배열 요소를 한번씩 순회하므로 N을 곱해주면 된다. 따라서 시간 복잡도는 O(NlogN)이 된다.
4. 정리
중앙 그리디 알고리즘이 계산하는 최대 넓이 직사각형은 다음 두 가지 종류밖에 없다.
1) 두 구역을 걸쳐있는 직사각형
2) 한 구역에만 걸쳐있는 직사각형
만약 중앙 그리디 알고리즘의 결과값이 한 구역에만 걸쳐있는 직사각형이 나온다면, 이것은 그 구역에 해당하는 분할 정복에서 이미 한번 고려된 값일 것이다. 반면 두 구역에 걸쳐있는 직사각형의 넓이가 새롭게 계산된다면, 이 값을 해당 구역을 대표하는 최대값으로 갱신될 가능성을 가진 완전히 새로운 값이라 볼 수 있다.
결국 반복하지만, 이 중앙 그리디 알고리즘의 결과가 한 구역만을 점유하는 직사각형이 되는 경우는 분할 정복 내에서 이미 고려가 됐을 것이라는 사실이 중요하다. 이는 다시 말해 '1) 두 구역을 걸쳐있는 직사각형' 의 계산 값만이 유용한 정보이다 고 볼 수 있다.
가장 처음에 적었던 경우의 수를 다시 살펴보자.
- 왼쪽 구역에서의 직사각형의 최대 넓이
- 오른쪽 구역에서의 직사각형의 최대 넓이
- 중간 경계에 걸쳐있는 직사각형의 최대 넓이
1번과 2번은 분할 정복으로 계산됐다. 중앙 그리디 알고리즘은 3번을 고려하기 위한 알고리즘이다. 앞서 살펴본 대로 중앙 그리디 알고리즘은 기묘하게도 위 경우 1,2,3을 모두 고려할 잠재성을 갖고 있지만, 실제 유용한 정보를 내놓는 경우는 3번밖에 없다. 다시 말해, 중앙 그리디 알고리즘은 '1번과 2번 경우는 잘 모르겠지만, 3번 경우에 한해서는 확실한 답을 내놓는다' 고 정리할 수 있다.
따라서 이상의 논리로 1, 2, 3 모든 경우가 온전하게 고려가 됐다고 볼 수 있다.
5. 코멘트
쓰고보니 너무 당연한 내용 같긴 한데 처음 문제를 봤을 때는 이렇게까지 고민해볼 수가 없었다. 그래도 글로 남기니 머리 속에서 어느 정도 정리가 되는 것 같다.
한편 그리디 알고리즘은 가장 간단하고 검사가 빠른 방법인 만큼, 문제를 풀 때는 항상 1순위로 고려해봐야 할 것 같다.