[알고리즘] | 부분집합(Subset)

부분집합이란?

집합에 포함된 원소들을 선택하는 것.

N개의 원소를 포함한 집합에서 부분집합을 찾는다고 생각해보자.

이 경우 자기자신과 공집합을 포함한 모든 부분집합(power set)의 개수는 2ⁿ개이다.

예를들어, {1, 2, 3, 4}의 집합이 있다고 가정하면 이 집합의 부분집합의 개수는 각 원소를 부분집합에 포함하는 경우 그리고 포함하지 않는 경우가 각각 존재하기 때문에 2*2*2*2 = 16 가지의 부분집합이 존재한다.

여기서 한가지 더 알수있는 사실은 부분집합의 개수는 집합의 원소의 수(n)가 증가하면 지수적으로 증가한다는 것이다.

부분집합 생성방법

1. 재귀와 방문처리를 사용한 부분집합 생성
2. 바이너리 카운팅을 사용하여 사전적 순서로 생성

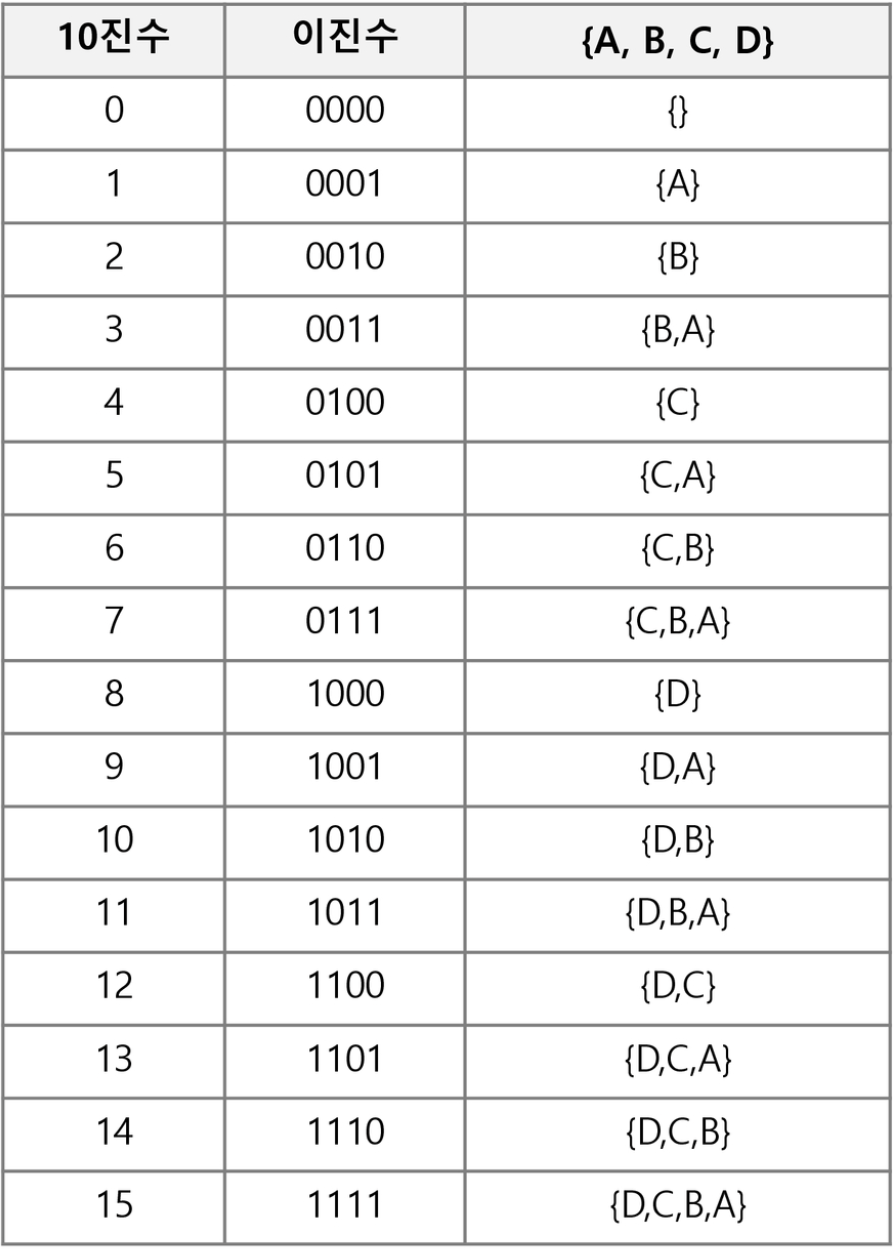
바이너리 카운팅을 사용한 부분집합 생성방법

1. 원소 수에 해당하는 N개의 비트열을 이용한다.
2. n번째 비트값이 1이라면 해당요소는 부분집합에 포함되었음을 의미한다.
   

예제코드

[재귀와 방문처리를 사용한 부분집합 생성]

public class SubsetTest {

    public static void main(String[] args) throws IOException {
        final BufferedReader bufferedReader = new BufferedReader(new InputStreamReader(System.in));
        final int inputNumberCount = Integer.parseInt(bufferedReader.readLine());

        final int[] input = new int[inputNumberCount];
        final boolean[] isSelected = new boolean[inputNumberCount];

        StringTokenizer stringTokenizer = new StringTokenizer(bufferedReader.readLine());

        for (int i = 0; i < inputNumberCount; i++) {
            input[i] = Integer.parseInt(stringTokenizer.nextToken());
        }

        generateSubset(input, isSelected, 0);
        System.out.println();
    }

    private static void generateSubset(final int[] input, final boolean[] isSelected, final int count) {
        if (count == input.length) {
            for (int i = 0; i < input.length; i++) {
                if (isSelected[i]) {
                    System.out.print(input[i] + " ");
                }
            }

            System.out.println();

            return;
        }

        isSelected[count] = true;
        generateSubset(input, isSelected, count + 1);
        isSelected[count] = false;
        generateSubset(input, isSelected, count + 1);

    }

}

[바이너리 카운팅을 사용한 부분집합 생성]

public class SubsetTest_Binary {

    public static void main(String[] args) throws IOException {
        final BufferedReader bufferedReader = new BufferedReader(new InputStreamReader(System.in));
        final int inputNumberCount = Integer.parseInt(bufferedReader.readLine());

        final int[] input = new int[inputNumberCount];

        StringTokenizer stringTokenizer = new StringTokenizer(bufferedReader.readLine());

        for (int i = 0; i < inputNumberCount; i++) {
            input[i] = Integer.parseInt(stringTokenizer.nextToken());
        }

        generateSubset(input);
        System.out.println();
    }

	// 만약 배열 input의 요소의 개수가 3일경우 부분집합이 나올 수 있는 경우의 수는 2의 3제곱 즉, 8이된다.
    // 경우의 수 8을 이용하여 0~7의 값을 비트마스킹으로 사용한다.
    // 000, 001, 010, 100, 011, 101, 110, 111
    // 3자리 비트중 비트가 1인 경우 해당 위치의 배열의 원소가 부분집합에 포함된 것이다.
    private static void generateSubset(final int[] input) {
		for (int i = 0; i < (1 << input.length); i++) {
            for (int j = 0; j < input.length; j++) {
                if((i & 1<<j) == 0){
                    continue;
                }

                System.out.print(input[j] +" ");
            }

            System.out.println();
        }

    }

}