순열이란?
서로 다른 것들 중 몇개를 뽑아서 한줄로 나열하는 것이다.
- 서로 다른 n개중 r개를 택하는 순열은
nPr이라고 표현한다. nPr은 다음 식이 성립한다.nPr = n * (n-1) * (n-2) * ... * (n-r+1)
nPn은n!이라고 표기하며 Factorial이라고 부른다.
순열을 생성하는 방법
- 재귀호출을 통한 순열 생성 (방문처리를 위해
boolean배열 사용) - 비트마스킹을 통한 순열생성 (정수와 비트연산자를 이용)
- 현 순열에서 사전순으로 다음 순열 생성 (NextPermutation)
비트마스킹을 통한 순열생성
- 순열의 첫번째 요소를 반복문을 돌면서 선택한다.
- 순열의 다음 요소를 선택한다. 이때,
flag변수를 사용해 이미 선택된 원소인지 확인한다. (자료형의 bit개수만큼 숫자의 사용여부를 판단할 수 있다.)
2-1.and연산과shift연산을 통해flag가0인지 확인해준다. (조건판단)
2-2.flag가0일경우 해당 원소는 이미 순열에 포함된 원소이므로 선택하지 않고 넘어간다.
2-3. 다음 원소를 선택하기 위해 다시 함수를 호출한다. 이때,or연산을 통해 기존 비트열(flag)에 상태를 누적해준다. - 순열에 선택된 원소의 개수가 종료조건을 만족하면 종료한다.
NextPermutation을 이용한 순열생성
- 주어진 배열을 오름차순으로 정렬해 가장 작은 순열을 한번에 처리한다.
- 사전순으로 다음으로 큰 순열을 생성한다. (가장 큰 내림차순 순열을 만들때까지 반복한다.)
2-1. 뒤쪽부터 탐색하면서 교환위치(i - 1)를 찾는다. (꼭대기i-> 가장 큰i)
2-2. 뒤쪽부터 탐색하면서 교환위치(i - 1)와 교환할 큰 값(j) 즉,i-1보다 큰 값을 갖는 위치를 찾는다. 이때,array[i-1] < array[i]이기 떄문에j를 못찾는 경우는 없다.
2-3. 두 위치값(i - 1,j)을 교환한다.
2-4. 다음 순열을 찾기위해 현재 꼭대기 위치(i)부터 맨뒤까지 오름차순 정렬한다.
만약, 주어진 배열이
5 4 3 2 1이라면0번째 인덱스인5가 꼭대기가 된다. 즉, 꼭대기가0번째 인덱스가 되는 순간이 순열의 마지막 순서이다.
또한, 항상 다음순열이 되는 값의 특징은 이전 순열보다 값이 크다.
NextPermutation을 이용한 순열 생성의 장단점
- 장점:
- 재귀로 짜여진 순열과 달리 시간복잡도가 낮다.
- 순열과 조합을 모두 사용할 수 있다.
- 단점:
- nPr과 같이 특정 개수의 숫자를 뽑아 순열을 만드는 것이 불가능하다.
순열 생성 시간복잡도
- 재귀와 방문처리를 이용한 순열 생성 시간복잡도:
O(n!) - NextPermutation을 이용한 순열 생성 시간복잡도:
O(n)
순열 사용시 주의사항
n개의 요소들에 대하여n!개의 순열이 존재하는데 이때n>12인 경우, 시간복잡도가 엄청나게 증가한다. 따라서n의 크기를 잘 확인해야한다.
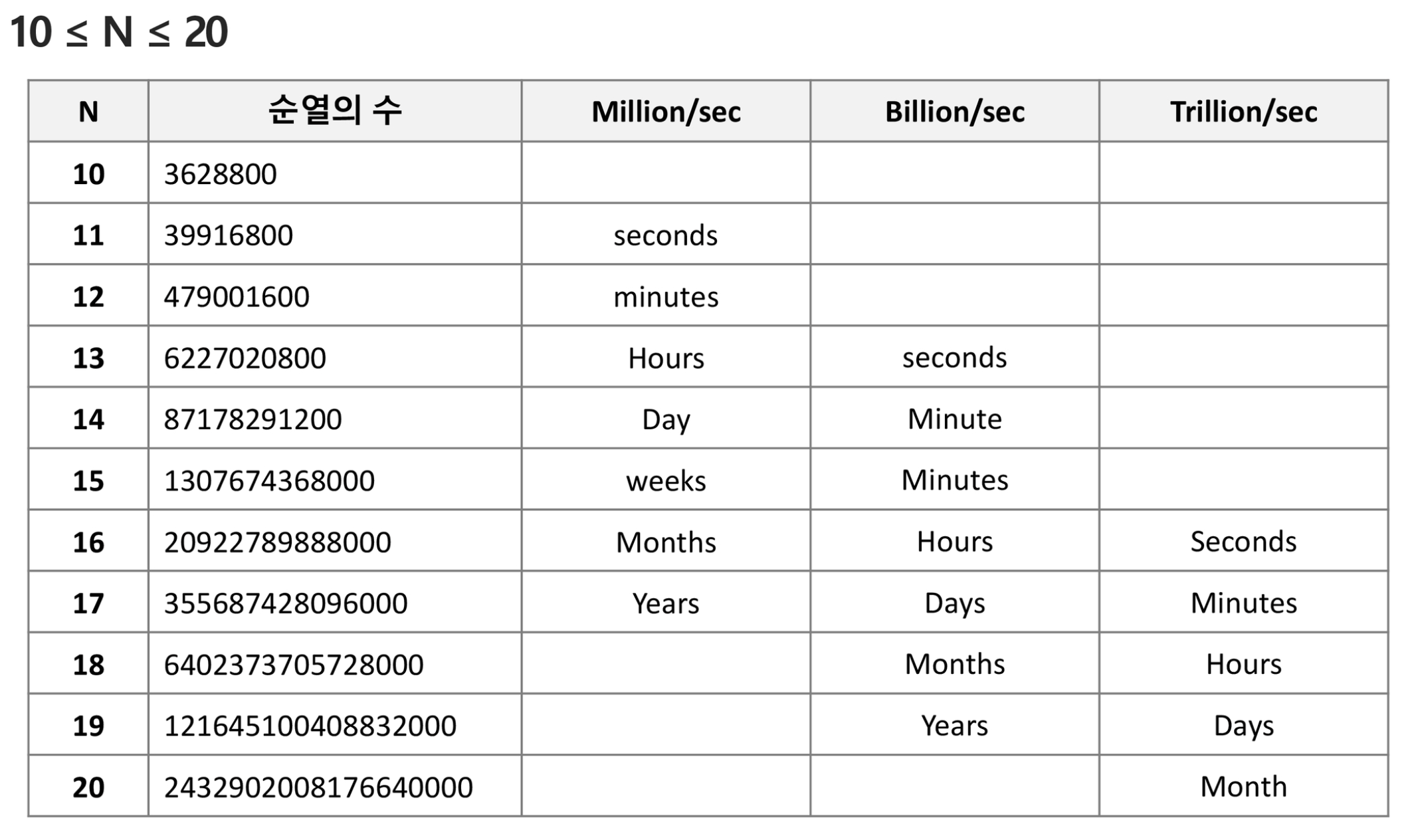
예제코드
[재귀호출을 통한 순열생성 예제코드]
public class PermutationTest {
public static void main(String[] args) throws IOException {
final BufferedReader bufferedReader = new BufferedReader(new InputStreamReader(System.in));
final int numberCount = Integer.parseInt(bufferedReader.readLine());
// 전체 숫자 개수
final int permutationCount = Integer.parseInt(bufferedReader.readLine());
// 뽑아야하는 숫자
final int[] input = new int[numberCount];
final boolean[] isSelected = new boolean[numberCount];
final int[] permutation = new int[permutationCount];
final StringTokenizer stringTokenizer = new StringTokenizer(bufferedReader.readLine());
for (int i = 0; i < numberCount; i++) {
input[i] = Integer.parseInt(stringTokenizer.nextToken());
}
makePermutation(input, permutation, isSelected, 0);
}
private static void makePermutation(final int[] input, final int[] permutation, final boolean[] isSelected, final int count) {
// 해당숫자가 수열을 생성하는데 사용되었는지 확인하는 사용여부를 체크하는 배열을 사용한다.
if (count == permutation.length) {
System.out.println(Arrays.toString(permutation));
return;
}
for (int i = 0; i < input.length; i++) {
if (isSelected[i]) {
continue;
}
permutation[count] = input[i];
isSelected[i] = true;
makePermutation(input, permutation, isSelected, count + 1);
isSelected[i] = false;
}
}
}
[비트마스킹을 통한 순열생성 예제코드]
public class PermutationTest_Bitmask {
public static void main(String[] args) throws IOException {
final BufferedReader bufferedReader = new BufferedReader(new InputStreamReader(System.in));
final int numberCount = Integer.parseInt(bufferedReader.readLine());
final int permutationCount = Integer.parseInt(bufferedReader.readLine());
final int[] input = new int[numberCount];
final int[] permutation = new int[permutationCount];
final StringTokenizer stringTokenizer = new StringTokenizer(bufferedReader.readLine());
for (int i = 0; i < numberCount; i++) {
input[i] = Integer.parseInt(stringTokenizer.nextToken());
}
makePermutation(input, permutation, 0, 0);
}
private static void makePermutation(final int[] input, final int[] permutation, final int count, final int flag) {
// flag: 선택된 원소에 대한 비트정보를 표현하는 정수
부를 확인한다.
if (count == permutation.length) {
System.out.println(Arrays.toString(permutation));
return;
}
for (int i = 0; i < input.length; i++) {
// 사용여부를 체크하는 boolean 배열대신 flag변수를 사용해 비트연산을 통해 사용여
if ((flag & 1 << i) != 0) {
// 해당 원소가 이미 순열에 사용되었다면 선택하지 않고 넘어간다.
// and 연산을 통해 순열에 사용되었는지 조건판단
continue;
}
permutation[count] = input[i];
makePermutation(input, permutation, count + 1, (flag | 1 << i));
// 해당원소를 선택했다면 해당 원소의 비트를 1로 마킹하고 다음 원소를 찾는다.
// or 연산으로 기존 비트열에 상태 누적.
}
}
}[NextPermuatation 통한 순열생성 예제코드]
public class PermutationTest_NextPer {
public static void main(String[] args) throws IOException {
final BufferedReader bufferedReader = new BufferedReader(new InputStreamReader(System.in));
final int numberCount = Integer.parseInt(bufferedReader.readLine());
final int[] input = new int[numberCount];
final StringTokenizer stringTokenizer = new StringTokenizer(bufferedReader.readLine());
for (int i = 0; i < numberCount; i++) {
input[i] = Integer.parseInt(stringTokenizer.nextToken());
}
Arrays.sort(input);
do {
System.out.println(Arrays.toString(input));
} while (makePermutation(input));
}
private static boolean makePermutation(final int[] input) {
int i = input.length - 1;
// 뒤쪽부터 탐색하며 교차점 찾기
while (i > 0 && input[i - 1] >= input[i]) {
i--;
}
// i = 0이면 순열을 생성하지 않는다.
// i = 0이라는 것은 순열이 내림차순 형태로 정렬되있다는것을 의미한다.
if (i == 0) {
return false;
}
// 뒤쪽부터 탐색하며 꼭대기 바로 앞자리의 값을 크게만들 교환할 값을 찾는다.
int j = input.length - 1;
while (input[i - 1] >= input[j]) {
j--;
}
// i-1번째 값과 j번째 값을 교환한다.
swap(input, i - 1, j);
// i 이후의 값들을 가장 작은 형태의 오름차순으로 정렬한다.
int k = input.length - 1;
while (i < k) {
swap(input, i++, k--);
}
return true;
}
private static void swap(final int[] input, final int i, final int j) {
int temp = input[i];
input[i] = input[j];
input[j] = temp;
}
}