🔥 학습목표
- 알고리즘이 무엇인지, 알고리즘의 일반적 특성에 대해 생각해본다.
- 알고리즘의 표현 방법에 대해 알아본다.
- 알고리즘을 분류해본다.
- 알고리즘에서 의미하는 효율성과 복잡도 표기에 대해 공부한다.
다음주 월요일 부터 알고리즘 스터디를 시작하기 전에...
먼저 알고리즘에 대한 선행 개념을 다시 점검하고 복습하는 시간을 가져야겠다.
🟣 알고리즘이란
⬜ 알고리즘
- 문제를 해결하는 단계적 절차 또는 방법
- 알고리즘에는 입력이 주어지고, 알고리즘은 수행한 결과인 해를 출력한다.
⬜ 보통 말로 알고리즘을 표현한다면...
최대 숫자 찾기 알고리즘을 보통 사람 말로 표현한다고 생각해보자.
- 카드의 숫자를 하나씩 비교하면서 본 숫자들 중 가장 큰 숫자를 기억해가며 찾는다.
- 마지막 카드의 숫자를 본 후, 머릿속에 기억된 가장 큰 숫자 카드를 집어 든다.
- 첫 카드의 숫자를 읽고 머릿속에 기억해둔다.
- 다음 카드의 숫자를 읽고 머릿속 숫자와 빕교한다.
- 비교 후 더 큰 숫자를 기억한다.
- 다음에 읽을 카드가 남아있으면 2번으로 이동한다.
- 머릿속에 기억된 숫자가 가장 큰 숫자다.
⬜ 의사코드로 표현한다면...
- max = A[0]
- for i = 1 to 9
- if (A[i] > max) max = A[i]
- return max
🟣 알고리즘의 분류
앞으로 아래와 같은 순서대로 알고리즘을 복습할 예정이다.
⬜ 문제 해결 방식에 따른 분류
-
분할 정복(Dicide-and-Conquer) 알고리즘
-
그리디(Greedy) 알고리즘
-
동적 계획(Dynamic Programming) 알고리즘
-
근사(Approximation) 알고리즘
-
백트레킹(Backtracking) 알고리즘
-
분기 한정 (Branch-and-Bound) 알고리즘
🟣 알고리즘의 효율성 표현
⬜ 알고리즘의 효율성
-
알고리즘의 수행시간 또는 알고리즘이 수행하는 동안 사용되는 메모리 크기
-
시간 복잡도(time complexitly), 공간 복잡도(space complexity)
-
일반적으로 알고리즘을 비교할 때는 시간 복잡도가 주로 사용 된다.
⬜ 시간 복잡도
알고리즘이 실행되는 동안 사용된 기본적인 연산 횟수를 입력 크기의 함수로 나타낸 것
- 기본 연산이란?
데이터 간 크기 비교, 데이터를 읽는 횟수, 변수 갱신, 숫자 계산 등과 같은 단순 연산을 의미한다.
Ex. 10장의 숫자 카드 중에서 최대 숫자를 찾기
- 순차 탐색의 경우 기본 연산은 숫자 비교다. 총 비교 횟수는 9번이다.
- n장의 카드가 있다면 (n-1)번의 비교 수행을 한다.
- 시간 복잡도는 (n-1) 이다.
🟣 복잡도의 점근적 표기
⬜ O(Big-Oh)-표기
정의
모든 n≥n0 에 대해서 f(n)≤cg(n)이 성립하는 양의 상수 c와 n0가 존재하면, f(n)=O(g(n))이다.
n0: 특정 자연수f(n): 원래 시간복잡도g(n): 점근적 표기
의미
n0와 같거나 큰 모든 n에 대해서 f(n)이 cg(n)보다 크지 않다는 것.
즉, n0보다 큰 모든 n에 대해서 f(n)이 양의 상수를 곱한 cg(n)에 미치지 못 한다는 뜻이다.
이때 g(n)을 f(n)의 상한(Upper Bound)이라고 한다.
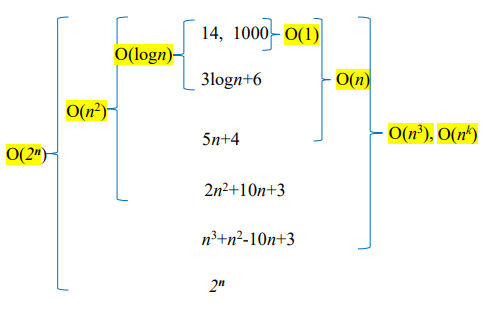
⬜ O-표기법 찾는 간단한 방법
다항식에서 최고 차수 항 만을 취한 뒤, 그 항의 계수를 제거하여 g(n)을 정한다.
f(n) = 2n2 - 8n + 3 의 경우 f(n)의 O-표기는 O(n2)
⬜ 자주 사용하는 O-표기

⬜ O-표기의 포함 관계