Binary Tree

Tree Operation

노드의 개수 세기

• 노드의 개수를 세기 위해서는 트리의 모든 노드를 순회해야함
• Traversal에서와 마찬가지로 자기 자신, left와 right노드를 재귀적으로 탐색

int getCount(BinaryNode *node)
{
	if(node == null) return 0;
    //자기 자신을 추가하기 위해 1을 더함
    return 1 + getCount(node->getLeft()) + getCount(node->getRight());
}

Leaf 노드 개수 세기

• leaf노드는 자식 노드를 갖지 않는 노드이므로 본인이 leaf 노드라면 1을 반환하고, 그렇지 않다면 재귀적으로 탐색을 이어감
• leaf노드 직전 노드에서 자신의 자식 노드를 탐색하면 자식 노드에서 1을 반환하므로 이를 leaf노드 개수에 추가

int getLeafCount(BinaryNode *node)
{
	if(node == null) return 0;
    if(node->isLeaf()) return 1;
    return getLeafCount(node->getLeft()) + getLeafCount(node->getRight());
}

Tree 높이 계산

• Tree의 높이는 Subtree의 높이 + 1
  (재귀적으로 적용하기 유리함)
• left와 right의 Subtree의 높이를 모두 구하되 둘 중 더 큰 값만 가져옴
• 높이가 1인 Subtree를 만날 때까지 재귀 탐색을 실시 후 연쇄적으로 값을 반환하며 종료됨

  높이가 3인 Perfect Binary Tree 예시

  1. root에서 출발
  2. getHeight(root->left) 호출
     2-1) 자식 노드가 존재하므로 getHeight(left->left) 호출
     2-1-1) 동일하게 getHeight(left->left) 호출하나 자식노드가 없어 바로 0이 반환 됨
     2-1-2) getHeight(left->right) 또한 자식노드가 없으므로 0이 반환
     2-1-3) return 1 + max(0,0) 이므로 1이 반환
     2-2) getHeight(left->left)가 1을 반환
     2-3) getHeight(left->right)를 호출
     2-3-1) getHeight(right->left)를 호출하나 0을 반환
     2-3-2) getHeight(right->right) 또한 0을 반환
     ([2-1] 내부의 과정과 동일)
     2-3-3) return 1 + max(0,0) 이므로 1이 반환
     2-4) getHeight(left->right)가 1을 반환
     2-5) 최종적으로 return 1 + max(1,1) 이므로 2가 반환
  3. 2번에서의 과정과 동일한 과정이 getHeight(root->right)에서 진행되었고, 최종적으로 2를 반환
  4. return 1 + max(2,2)이므로 최종적으로 3을 반환

Tree의 활용

Expression Tree

• 후위 연산자, 중위 연산자 등에서 사용했던 방식을 Tree를 통해 표현할 수 있음

• Preorder는 전위 연산, Inorder는 중위 연산, Postorder는 후위 연산에 대응

  예시

  
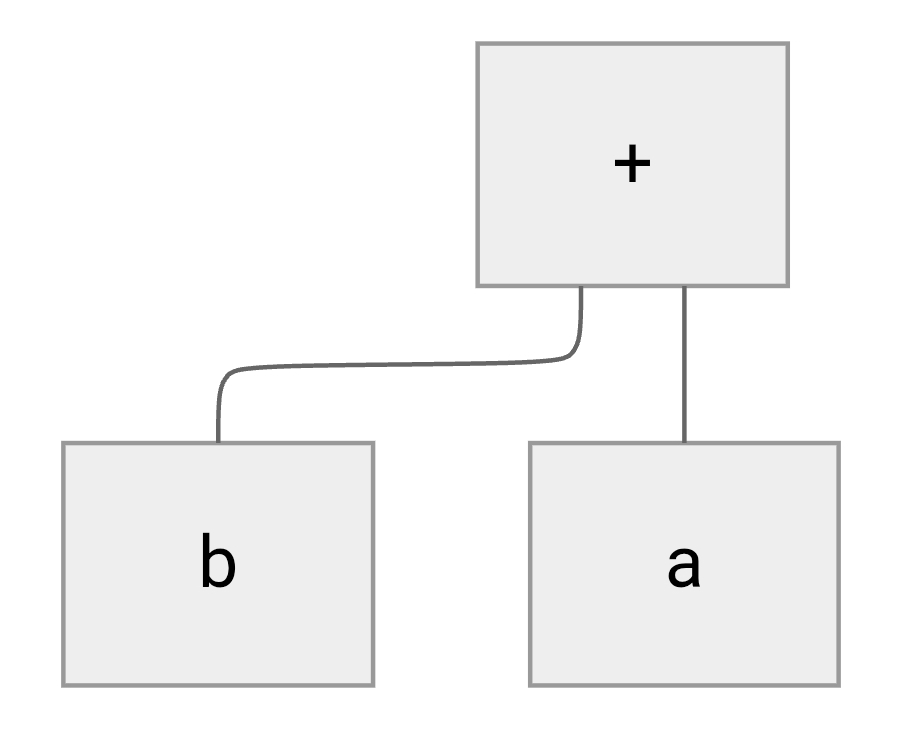
  Preorder : +ab
  Inorder : a+b
  Postorder : ab+

• 연산식에서 괄호는 Subtree로 표현할 수 있음

  예시

  
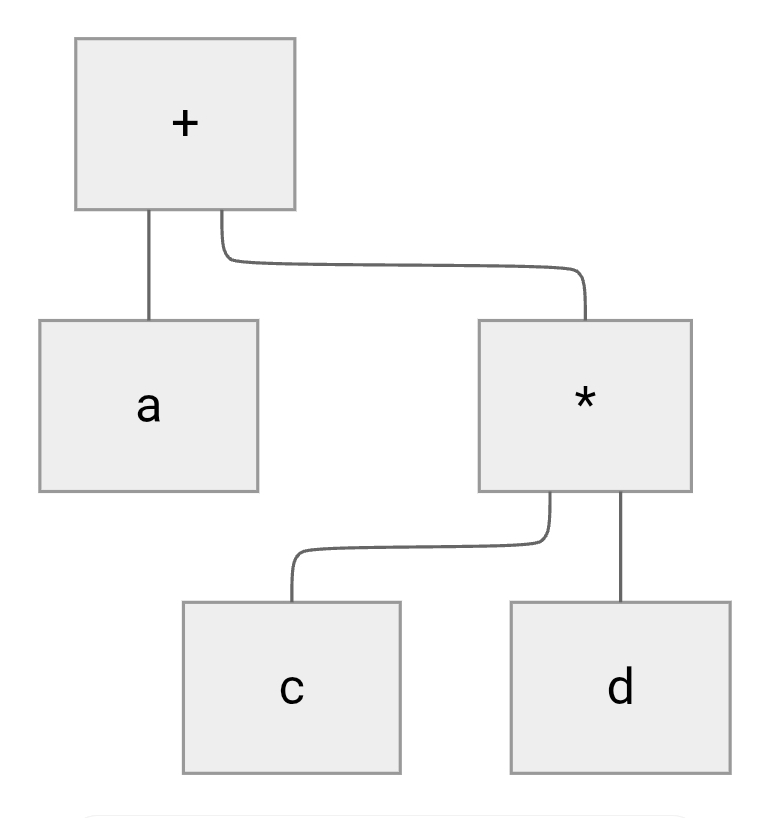
  a + (c d)
  Preorder : + a cd
  Inorder : a + c d
  Postorder : acd+

• root 노드는 연산자 역할을 하고 Subtree들이 피연산자역할을 수행

• 괄호를 고려한 연산 순서를 위해서는 Postorder를 사용한 연산이 필요

File Size Claculator

• 컴퓨터의 폴더 구조는 Tree를 통해 표현할 수 있음
  (일반적으로 Binary Tree 구조는 아니지만 이번 경우는 이진 트리로 가정함)
• leaf노드에서부터 각각의 노드의 크기를 측정해 전부 더한 값이 전체 파일의 크기로 볼 수 있음
• 따라서 Postorder 순회를 통해 파일 크기 구조 계산이 가능
  (Postorder는 root로 가기 전에 무조건 자식 노드들 전부 방문하므로)

Threaded Binary Tree

• Threaded Binary Tree란 기존에 재귀 방식을 사용하는 순회 방식과 다른 방법을 추가적으로 구현
• leaf노드의 null 링크들을 재활용함, null 링크들이 inorder predecessor 또는 successor를 가리키는데 사용됨
• 링크를 재활용하기 때문에 자식 노드를 가리키는 링크와 thread 필드를 가리키는 링크를 구분하는 것이 필요