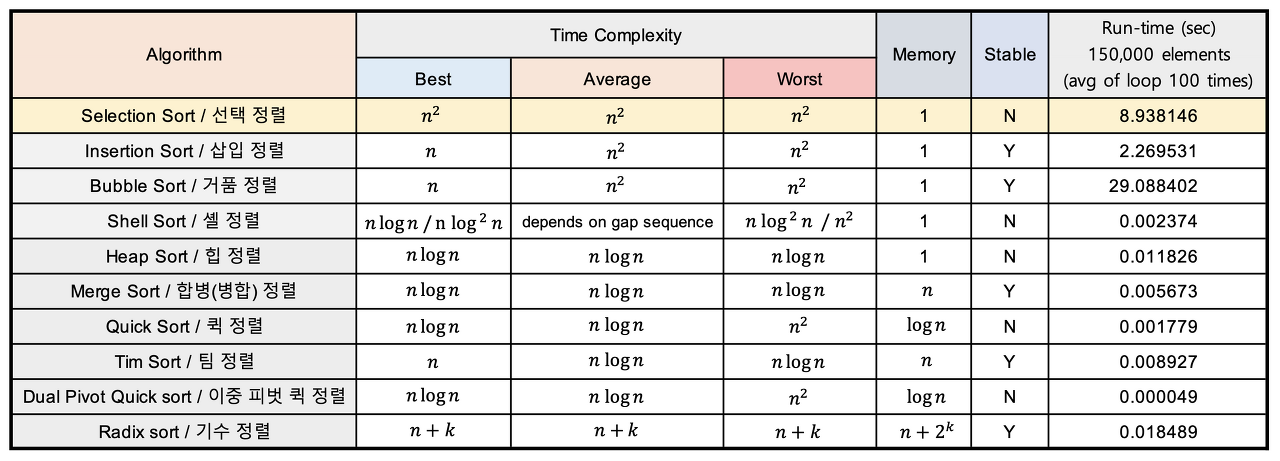
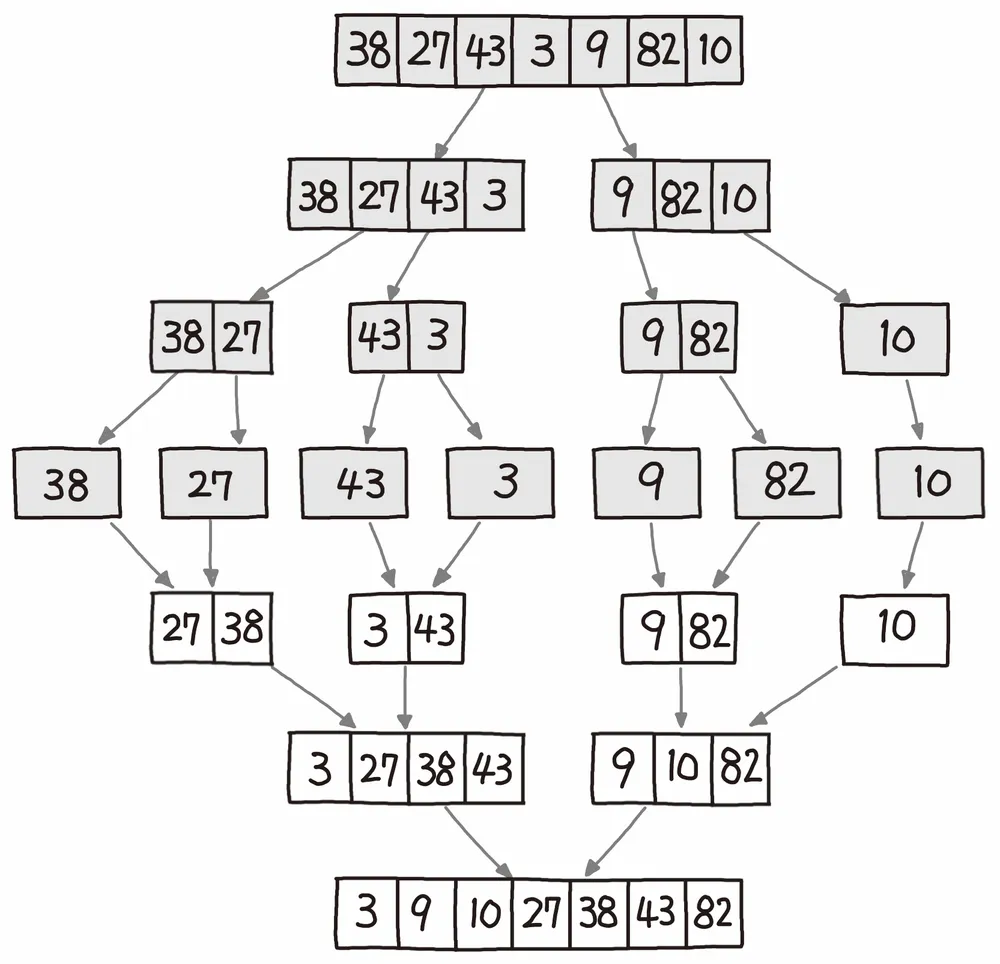
병합/합병정렬
Top-Down 형식
Bottom-Up 형식
병합/합병 정렬의 장단점
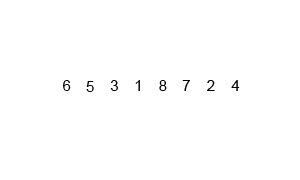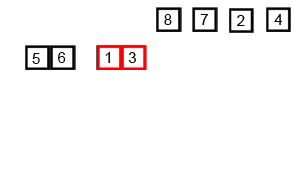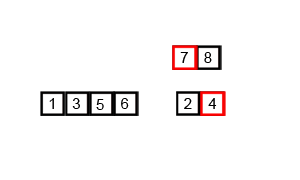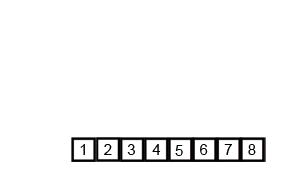
병합정렬
목차로이동
기본적으로 합병정렬은 '문제를 분할하고, 분할한 문제를 정복하여 합치는 과정'이다.
합병정렬은 기본적으로 '분할 정복' 알고리즘을 기반으로 정렬되는 방식이다.
Top-Down 형식의 병합정렬은 재귀를 사용해서 이루어지는 정렬입니다.
병합정렬의 구조상 최대한 작게 문제를 쪼개어 앞의 부분리스트부터 차례대로 합쳐나가기 때문에 안정정렬(Stable Sort) 알고리즘이기도 하다.
힙이나 퀵의 경우에는 배열 A[25]=100, A[33]=100인 정수형 배열을 정렬한다고 할 때, 33번째에 있던 100이 25번째에 있던 100보다 앞으로 오는 경우가 생길 수 있다.
그에 반해서 병합정렬은 이런 일이 발생하지 않는다. 기본적으로 병합정렬은 쪼갠 후 두 값을 비교할 때 값이 같으면 정렬하지 않게 설계되기 때문이다.
그게 뭐가 중요하냐고 할 수 있지만, 실제 상황에서 여러 기준으로 정렬했을 때 동일 값에 대해선 기존 기준의 정렬순서가 유지되어야 한다.
정렬되어 있는 두 배열을 합집합할 때 이 알고리즘의 마지막 단계만을 이용하면 가장 빠르게 정렬된 상태로 합칠 수 있다.
Top-Down 형식
public class MergeSortTest{
public static void main(String[] args) {
MergeSort sort = new MergeSort;
int[] arr = { 38,27,43,3,9,82,10,5,1,55,37 };
sort.mergeSort(arr, 0, arr.length - 1);
for (int i : arr) {
System.out.print(i + " ");
}
}
}
public class MergeSort {
public static void mergeSort(int[] arr, int left, int right) {
if (left < right) {
int mid = (left + right) / 2;
mergeSort(arr, left, mid);
mergeSort(arr, mid + 1, right);
merge(arr, left, mid, right);
}
}
public static void merge(int[] arr, int left, int mid, int right) {
int[] temp = new int[right - left + 1];
int i = left, j = mid + 1, k = 0;
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {
temp[k++] = arr[i++];
} else {
temp[k++] = arr[j++];
}
}
while (i <= mid) {
temp[k++] = arr[i++];
}
while (j <= right) {
temp[k++] = arr[j++];
}
for (int p = 0; p < temp.length; p++) {
arr[left + p] = temp[p];
}
}
}
부분별로 살펴보자
우선 분할 하는 부분을 살펴보자.
public static void mergeSort(int[] arr, int left, int right) {
if (left < right) {
int mid = (left + right) / 2;
mergeSort(arr, left, mid);
mergeSort(arr, mid + 1, right);
merge(arr, left, mid, right);
}
}파라미터 부분
public static void mergeSort(int[] arr, int left, int right)int [] arr : 정렬할 배열
int left : 시작 지점(인덱스)
int right: 끝 지점(인덱스)
빠져나가기 위한 조건
if (left < right) 함수가 작동 시키기 위한 조건이며 재귀를 반복할 조건 설정
- 배열의 크기가 1보다 작거나 같으면 이미 정렬된 상태이므로 정렬할 필요가 없다.
int mid = (left + right) / 2;
mergeSort(arr, left, mid);
mergeSort(arr, mid + 1, right);
merge(arr, left, mid, right);mid는 배열의 중간값을 찾기위한 것
- 어느 부분을 기준으로 좌우로 나눌것인가
mergeSort(arr, left, mid);- 배열의 왼쪽 부분을 정렬하기 위해 mergeSort() 함수(메소드)를 재귀적으로 호출
mergeSort(arr, mid + 1, right);- 배열의 오른쪽 부분을 정렬하기 위해 mergeSort() 함수(메소드)를 재귀적으로 호출
merge(arr, left, mid, right);왼쪽과 오른쪽 부분을 정렬한 후, 두 부분을 병합
이제 병합하는 부분을 살펴보자
병합부분
public static void merge(int[] arr, int left, int mid, int right)
int[] temp = new int[arr.length];
int i = left;
int j = mid + 1;
int k = left;int[] arr : 병합해서 넣을곳
int left : 정렬된 배열의 시작 지점(인덱스)
int mid : 오른쪽 부분 시작 지점(인덱스)이 될것+1 하면됨
int right : 범위의 끝
int[] temp : 정렬된 배열을 저장할 임시 배열 temp를 생성
int i : 왼쪽 부분의 시작 인덱스
int j : 오른쪽 부분의 시작 인덱스
int k : 배열 temp의 시작 인덱스
여기서 왜 i랑 k는 같은데 나누는건가? 하는 의문이 있으실탠데
temp[k++] = arr[i++];
} else {
temp[k++] = arr[j++];내용을 보시면 시작 지점 위치는 달라지기 때문에 i와 k로 나눕니다.
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {
temp[k++] = arr[i++];
} else {
temp[k++] = arr[j++];
}
}while문을 이용하여 i(왼쪽 시작지점)이 mid(오른쪽 시작지점)보다 작거나 같고,
mid(오른쪽 시작지점)이 right(범위)보다 작을때까지 반복하면서
왼쪽과 오른쪽을 비교하면서 temp배열에 저장합니다.
while (i <= mid) {
temp[k++] = arr[i++];
}
while (j <= right) {
temp[k++] = arr[j++];
}위의 while문보다 먼저 시작한 while문에서 종료되었지만 오른쪽이 먼저 끝나거나 왼쪽이 먼저 끝났을경우 반대쪽(우측이면 좌측, 좌측이면 우측) 원소는 무조건 남아있기 때문에
우측 while(반복)문과 좌측 while(반복)문을 통하여 남은 원소들을 temp 배열에 넣어줍니다.
for (int index = left; index < k; index++) {
arr[index] = temp[index];
}마지막으로, 정렬한 temp 배열의 값을 arr 배열에 넣어줍니다.
Bottom-Up 형식
public class MergeSortTest{
public static void main(String[] args) {
int[] arr = { 38, 27, 43, 3, 9, 82, 10, 5, 1, 55, 37 };
MergeSortBottomUp sort = new MergeSortBottomUp();
sort.mergeSort(arr);
for (int i : arr) {
System.out.print(i + " ");
}
}
}
public class MergeSortBottomUp {
public void mergeSort(int[] arr) {
int n = arr.length;
int[] temp = new int[n];
for (int size = 1; size < n; size *= 2) {
for (int leftStart = 0; leftStart < n; leftStart += 2*size) {
int mid = Math.min(leftStart + size - 1, n - 1);
int rightEnd = Math.min(leftStart + 2*size - 1, n - 1);
merge(arr, temp, leftStart, mid, rightEnd);
}
}
}
public static void merge(int[] arr, int[] temp, int leftStart, int mid, int rightEnd) {
int i = leftStart,
int j = mid+1
int k = leftStart;
while (i <= mid && j <= rightEnd) {
if (arr[i] <= arr[j]) {
temp[k++] = arr[i++];
} else {
temp[k++] = arr[j++];
}
}
while (i <= mid) {
temp[k++] = arr[i++];
}
while (j <= rightEnd) {
temp[k++] = arr[j++];
}
for (i = left; i <= rightEnd; i++) {
arr[i] = temp[i];
}
}
}분할하는 부분
public void mergeSort(int[] arr)Bottom-Up방식은 Top-Down 방식과는 다르게 받는 파라미터가 정렬한 배열밖에 없다.
int[] arr: 정렬할 배열
int n = arr.length;
int[] temp = new int[n];int n : 배열의 크기
int[] temp : 정렬된 배열을 저장해둘 임시 배열
for (int size = 1; size < n; size *= 2) {
for (int leftStart = 0; leftStart < n; leftStart += 2*size) {
}
}첫번째 반복문의 size
merge할 두 부분 배열의 크기. 1, 2, 4, 8, ... 순서로 증가합니다.
두번째 반복문의 leftStart
merge할 왼쪽 부분 배열의 시작 인덱스.
이중 반복문 안의 내용
int mid = Math.min(leftStart + size - 1, n - 1);
int rightEnd = Math.min(leftStart + 2*size - 1, n - 1);
merge(arr, temp, leftStart, mid, rightEnd);int mid : 중간 인덱스
int rightEnd : 오른쪽 끝 인덱스(범위의 끝)
merge : merge 메소드를 호출하여 두 부분 배열을 합칩니다.
병합하는 부분
arr 배열의 leftStart부터 mid까지와 mid+1부터 rightEnd까지를
합쳐서 temp 배열에 저장합니다. temp 배열의 leftStart부터 rightEnd까지
해당 구간의 원소를 정렬된 상태로 arr 배열에 복사합니다.
private void merge(int[] arr, int[] temp, int leftStart, int mid, int right) {int[] arr : 정렬할 배열
int[] temp : 정렬된 내용을 임시 저장하는 배열
int leftStart : 왼쪽 부분 배열의 현재 인덱스
int mid : 왼쪽 부분 배열의 끝 인덱스
int rightEnd : 범위 종료
int i = leftStart,
int j = mid+1
int k = leftStart;int i : 왼쪽 부분 배열의 현재 인덱스
int j : 오른쪽 부분 배열의 현재 인덱스
int k : 병합한 배열의 현재 인덱스
while (i <= mid) {
temp[k++] = arr[i++];
}
while (j <= rightEnd) {
temp[k++] = arr[j++];
}
for (i = left; i <= rightEnd; i++) {
arr[i] = temp[i];
}위의 while문보다 먼저 시작한 while문에서 종료되었지만 오른쪽이 먼저 끝나거나 왼쪽이 먼저 끝났을경우 반대쪽(우측이면 좌측, 좌측이면 우측) 원소는 무조건 남아있기 때문에
우측 while(반복)문과 좌측 while(반복)문을 통하여 남은 원소들을 temp 배열에 넣어줍니다.
마지막으로, 정렬한 temp 배열의 값을 arr 배열에 넣어줍니다.
라는 식으로 merge의 경우 같은데 분할의 경우 분할 배열을 가져오는 것 정도만 다릅니다.
재귀를 쓰지않고 구현하는 형식이니까 나누는 부분만 다른겁니다.
대부분의 경우 정렬 과정은 최대한 재귀는 피하여 구현하는게 일반적이기 때문에 Bottom-Up 으로 구현하는 것이 좋다.
병합/합병 정렬의 장단점
장점
- 안정적인 정렬 알고리즘이며, 시간 복잡도가 O(n log n)으로 매우 효율적입니다.
- 배열의 길이와 관계없이 항상 O(n log n)의 시간 복잡도를 가지며, 데이터가 무작위인 경우에도 높은 성능을 보입니다.
- 데이터의 분포와 무관하게 동일한 시간복잡도를 가지므로, 퀵정렬과는 달리 최악의 경우 O(n log n)의 성능을 보장합니다.
단점
- 병합정렬은 임시 배열이 필요하므로, 메모리 사용량이 늘어납니다.
- 메모리 사용량이 중요하거나, 매우 큰 데이터의 경우 비효율적일 수 있다. - 상대적으로 구현이 복잡하고, 퀵정렬보다 느립니다.
- 병합 정렬은 내부 정렬로 구현될 수 없어, 대부분의 경우에는 외부 정렬로 사용됩니다.