3. 알고리즘 패러다임

1. Brute Force

bruce force attack 무차별 공격 - 가능한 모든 경우의 수를 모두 대입해서 문제를 해결

-input이 커질수록 비효율적임...!

두 카드그룹에서 각 곱셈값이 가장 큰 수 구하기→시간복잡도 O(mn)

def max_product(left_cards, right_cards):
    # 현재까지 최댓값을 담기 위한 변수
    # 처음에는 임시로 -1로 설정
    max_product = -1
    
    # 가능한 모든 조합을 보기 위한 중첩 반복문
    for left in left_cards:
        for right in right_cards:
            # 현재까지의 최댓값 값과 지금 보고 있는 곱을 비교해서 더 큰 값을 최댓값 변수에 담아준다
            max_product = max(max_product, left * right)

    # 찾은 최댓값을 리턴한다            
    return max_product

강남역 폭우 - 시간복잡도O(n^2)

trapping_rain(buildings):
    #총 담기는 빗물의 양을 변수에 저장
    total_height=0
    
    #리스트의 각 인덱스를 돌면서 해당 카에 담기는 빗물의 양을 구하기
    #0번과 마지막 인덱스는 어차피 물이 고일 수 없으니 배제
    for i in range(1, len(buildings)-1):
        #현재 위치의 양 옆에서 가장 높은 건물의 인덱스 찾음
        max_left=max(buildings[:i])
        max_right=max(buildings[i:])
        #현재 인덱스에서 빗물이 담길 수 있는 높이(양옆max인덱스 중 작은수-현재인덱스의 높이)
        upper_bound = min(max_left, max_right)
        #만약 upper_bound가 현재 인덱스 건물보다 낮으면 현재 인덱스에 담기는 빗물 0
        total_height += max(0, upper_bound-buildings[i])
    return total_height

print(trapping_rain([0, 3, 0, 0, 2, 0, 4]))                #10
print(trapping_rain([0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1])) #6

2. Divide and conquer(분할정복)

• 재귀개념을 빠삭하게 이해하고 있어야 한다

• DIvide - 문제를 작게 나눔

  Conquer - 분할한 문제를 해결(정복)

  Conbine - 해결한 분할문제들을 합쳐서 큰 문제 해결

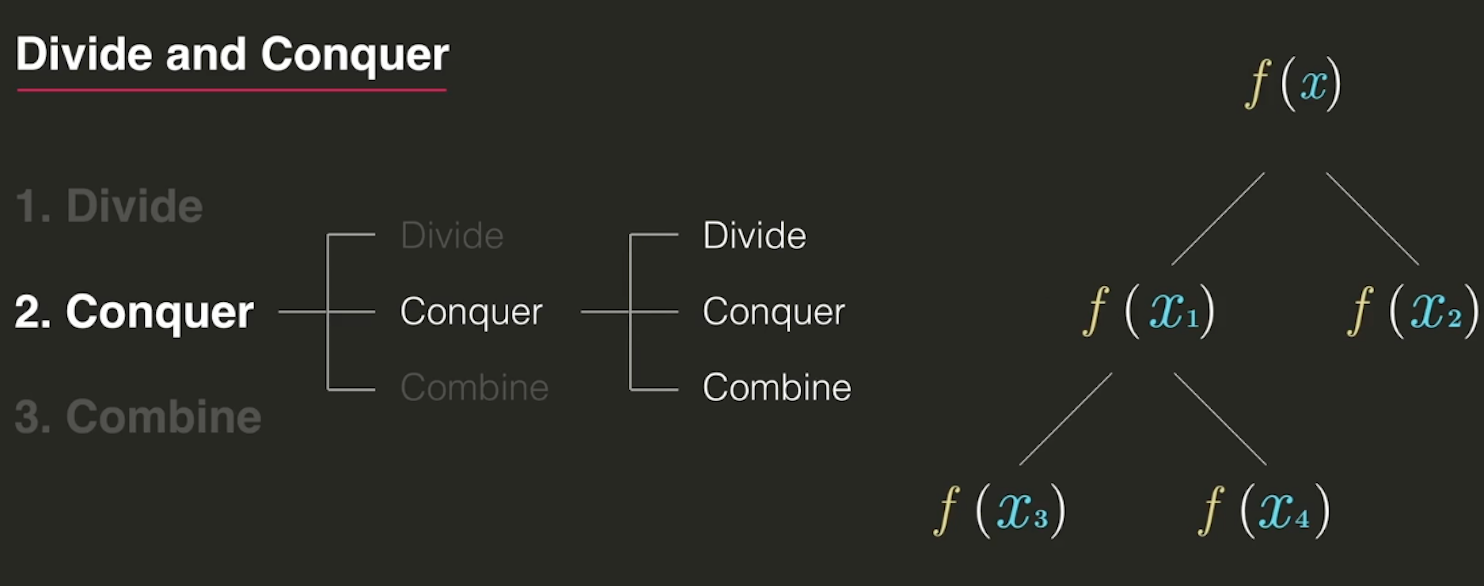
1~n까지의 합 구하기

시간복잡도: n + 1/2n + 1/4n + 1/8n +... = (1+1/2+1/4+1/8...)n = 2 ⇒ O(2n) ⇒ O(n)

def consecutive_sum(start, end):
    if start==end:
        return start
    else:
				#consecutive_sum의 return값을 더하여 combine하므로 분할정복으로 생각
				#더이상 쪼개지지 않는 1숫자까지 나눠진 값이 더해짐
        return consecutive_sum(start,(start+end)//2) + consecutive_sum((start+end)//2+1, end)
    
print(consecutive_sum(1, 10))   #50
print(consecutive_sum(1, 100))  #5050

• 합병 정렬(Merge sort)

  Divide 리스트를 반으로 나눈다

  Conquer 왼쪽, 오른쪽 리스트를 각각 정렬한다

  Combine 정렬된 두 리스트를 하나의 정렬된 리스트로 합병한다

def merge(list1, list2):
    merged_list=[]
    i=0
    j=0
    while i<len(list1) and j<len(list2):
        if list1[i] < list2[j]:
            merged_list.append(list1[i])
            i+=1
        else:
            merged_list.append(list2[j])
            j+=1
#     위의 while문은 list1나 list2가 소진되면 끝남!!
#     남은 항목이 있으면 정렬 리스트에 추가!!!! (리스트 범위를 i,j이후부터로 지정!!)    
    merged_list=merged_list+list1[i:]+list2[j:]
    return merged_list

정렬된 리스트를 병합하는 함수 merge
def merge(list1, list2):
    i=0
    j=0
    merged_list=[]
    
    while i<len(list1) and j<len(list2):
        if list1[i]<list2[j]:
            merged_list.append(list1[i])
            i+=1
        else:
            merged_list.append(list2[j])
            j+=1
            
     # list2에 남은 항목이 있으면 정렬 리스트에 추가
    if i==len(list1):
        merged_list+=list2[j:]
    # list1에 남은 항목이 있으면 정렬 리스트에 추가
    elif j==len(list2):
        merged_list+=list1[i:]
        
    return merged_list

#리스트를 나눠서 정렬하는 병합정렬 합수 merge_sort
def merge_sort(my_list):
    #base case: 리스트 개수가 0,1개라서 정렬을 안 해도 되는 상태
    if len(my_list)<2:
        return my_list
    #my_list를 반씩 나누기(divide)
    left_half=my_list[:len(my_list)//2]
    right_half=my_list[len(my_list)//2:]
    #merge_sort함수를 재귀적으로 호출->부분문제해결(conquer)
    #merge함수로 정렬된 두 리스트를 합친다(combine)
    return merge(merge_sort(left_half),merge_sort(right_half))

• 퀵 정렬

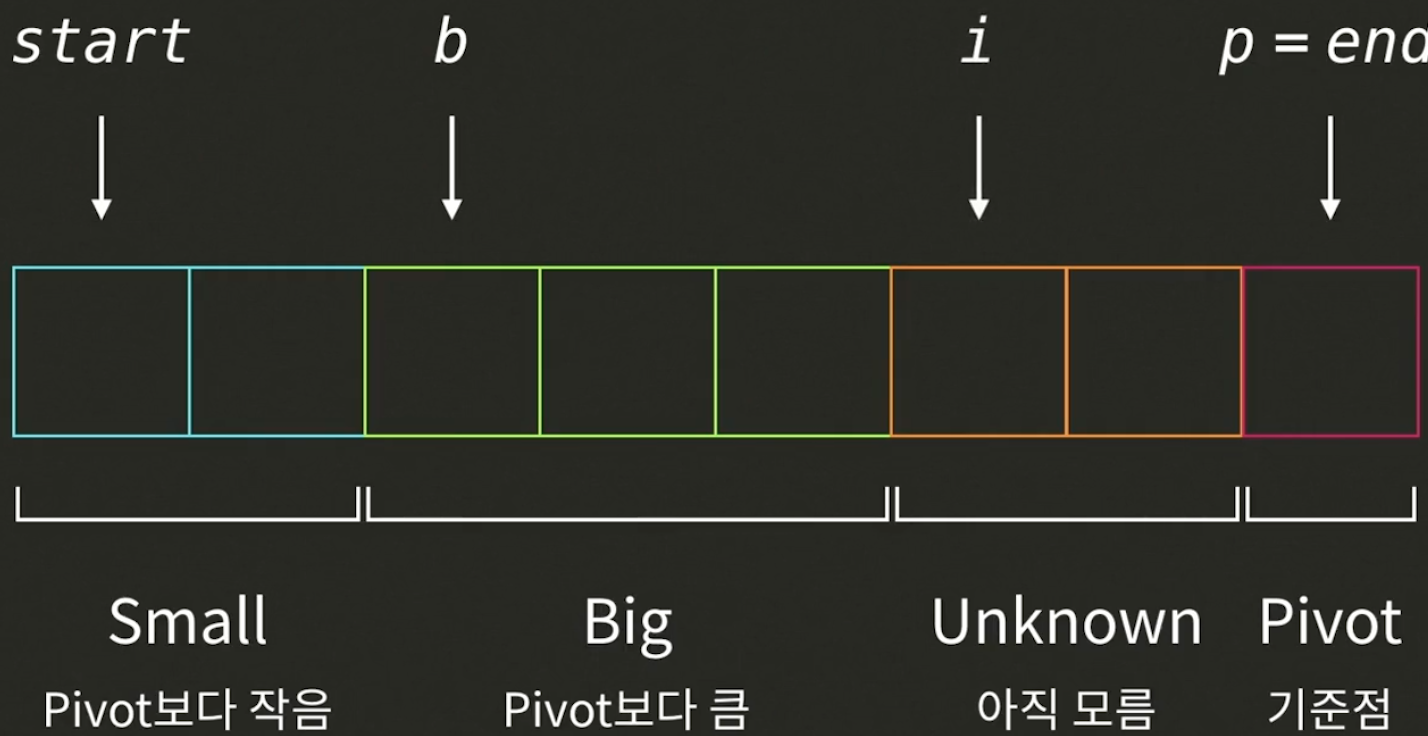
# 두 요소의 위치를 바꿔주는 helper function
def swap_elements(my_list, index1, index2):
    temp = my_list[index1]
    my_list[index1] = my_list[index2]
    my_list[index2] = temp
		#my_list[index1],my_list[index2]=my_list[index2],my_list[index1]

# 퀵 정렬에서 사용되는 partition 함수
def partition(my_list, start, end):
    # 리스트 값 확인과 기준점 이하 값들의 위치 확인을 위한 변수 정의
    i=start   #리스트를 돌며 검사하는 인덱스
    b=start   #pivot보다 큰수의 첫번째값
    p=end     #마지막 수를 pivot으로 설정

    # 범위안의 모든 값들을 볼 때까지 반복문을 돌린다
    while i < p:
        # i 인덱스의 값이 기준점보다 작으면 i와 b 인덱스에 있는 값들을 교환하고 b를 1 증가 시킨다
        if my_list[i] <= my_list[p]:
            swap_elements(my_list, i, b)
            b += 1
        i += 1

    # b와 기준점인 p 인덱스에 있는 값들을 바꿔준다->p의 양옆으로 p보다 작은수,큰수가 나뉨
    swap_elements(my_list, b, p)
    p = b

    # pivot의 최종 인덱스를 리턴해 준다
    return p

# 퀵 정렬
def quicksort(my_list, start=0, end=None):
    # base case
    #end-start값이 음수인 경우를 고려해서 (<1)로 범위를 설정함!!
    #파이썬 리스트는 mutable하므로 함수 안에서 수정해도 바깥에서 접근했을 때 수정된 상태를 확인할 수 있다. 수정된 리스트를 return하지 않아도 외부에서 확인,변경 가능하므로 따로 return값에 리스트를 적지 않는다
    if end==None:
        end = len(my_list)-1
    
    if end - start < 1:
        return 

    # my_list를 두 부분으로 나누어주고,
    # partition 이후 pivot의 인덱스를 리턴받는다
    pivot = partition(my_list, start, end)
    # pivot의 왼쪽 부분 정렬
    quicksort(my_list, start, pivot - 1)
    # pivot의 오른쪽 부분 정렬
    quicksort(my_list, pivot + 1, end)

(+)파이썬 옵셔널 파라미터

#함수 파라미터를 따로 설정하지 않아도 미리 지정한 기본값이 들어가서 함수를 실행시킴
#기본값 None의 의미: 파라미터를 따로 전닯받지 못했지만 None을 넣겠다

def func1(p1,p2,p3=0,p4=None):
    print(p1,p2,p3,p4)
    
func1(2,3,4,5)
func1(7,8)

3. Dynamic Programming

• 조건
  1. 최적 부분 구조(Optimal Substructure): 부분 문제들의 최적의 답을 이용해서 기존 문제의 최적의 답을 구할 수 있다는 것 ex.피보나치 수열, 서울~부산 최단거리
  2. 중복되는 부분문제(Overlapping Subproblems): 중복되는 부분문제를 여러번 푸는 것은 비효율적임. 이를 해결하기위해 dynamic programming을 활용
• Dynamic Programming
  • 한 번 계산한 결과를 재활용하는 방식
  • 시간복잡도: O(n)
    • 호출하는 함수의 개수만큼 해당됨

1. Memoization

• 중복되는 계산은 한 번만 계산 후 메모리에 저장해두는 방식
• 하향식 접근(Top-down Approach)
• 재귀함수 사용

ex.피보나치 수열

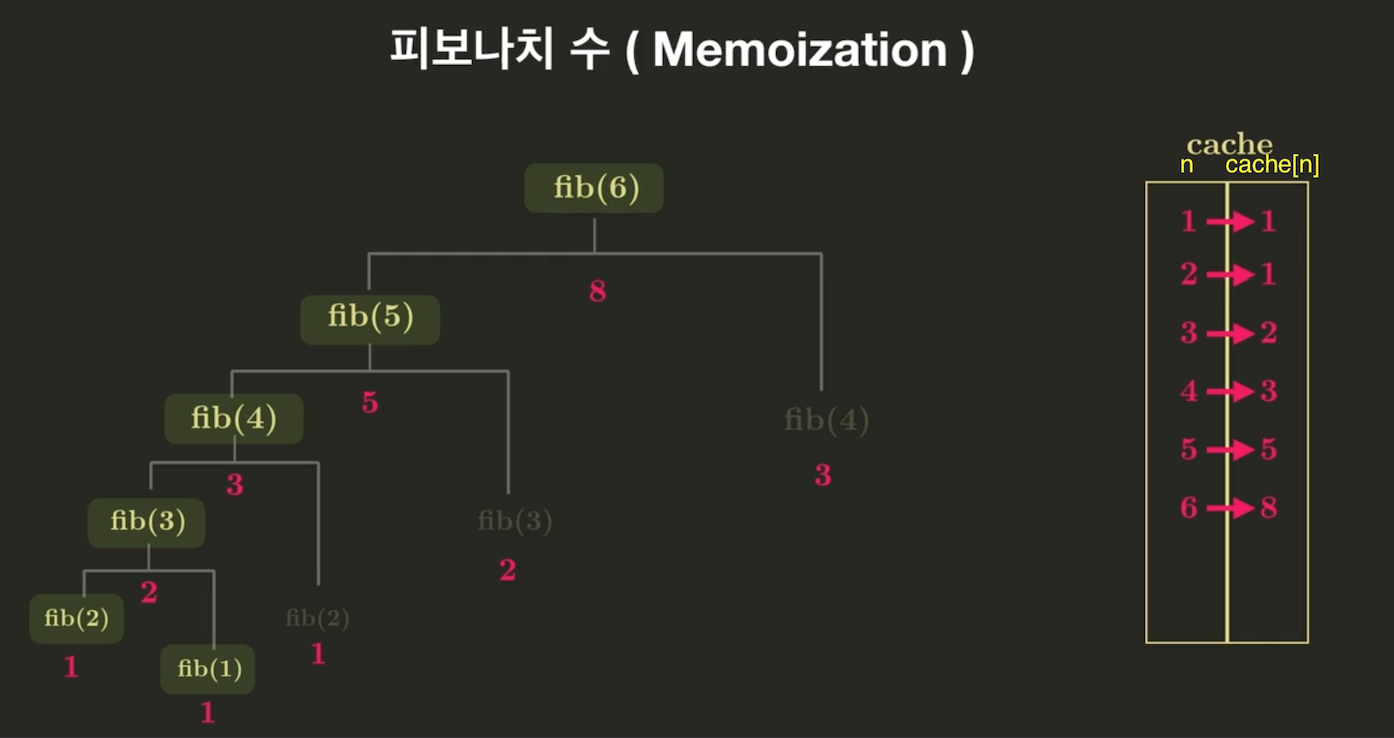
• base case: n=1,2일때는 return 1
• recursive case: 이미 n번째 피보나치 수를 계산할 경우(cache[n]이 존재하는경우 값 return) / 아직 n번째 피보나치 수를 계산하지 않은 경우(cache[n]이 존재하지 않는 경우 계산해서 cache에 저장)

• ver 코드잇

    def fibo_memo(n, cache):
    	#base case
    	if n<3:
    	        return 1

    	#이미 n번째 피보나치를 계산했다면: 저장된 값을 바로 리턴
    	if n in cache:
    		return cache[n]  

    	#아직 n번째 피보나치 수를 계산하지 않았으면: 계산 후 cache에 저장
    	cache[n] = fibo_memo(n-1, cache)+fibo_memo(n-2,cache)
    	#계산한 값을 리턴
    	return cache[n]

    def fib(n):
    	#n번째 피보나치 수를 담는 딕셔너리
    	fib_cache={}
    	return fibo_memo(n, fib_cache)

    #test
    print(fib(10))  #55

• ver이코테

# 한 번 계산된 결과를 메모이제이션하기 위한 리스트 초기화
d = [0] * 100

# 탑다운 다이내믹 프로그래밍
def fibo(x):
	# 종료 조건(1 또는 2일 때 1 반환)
   if x==1 or x==2:
    	return 1
    # 이미 계산한 적 있는 문제라면 그대로 반환
    if d[x] != 0:
    	return d[x]
    # 아직 계산하지 않은 문제라면 점화식에 따라 피보나치 결과 반환
    d[x] = fibo(x-1) + fibo(x-2)
    return d[x]
    
 print(fibo(99))

위 코드 실행 시 호출되는 함수 순서: f(99) f(98) ... f(2) f(1) f(1) f(3) ... f(97) 

2. Tabulation

• 상향식 접근(Bottom-up Approach)
• Table방식(표를 채우는 듯한 과정)
• 반복문 사용(재귀함수x)

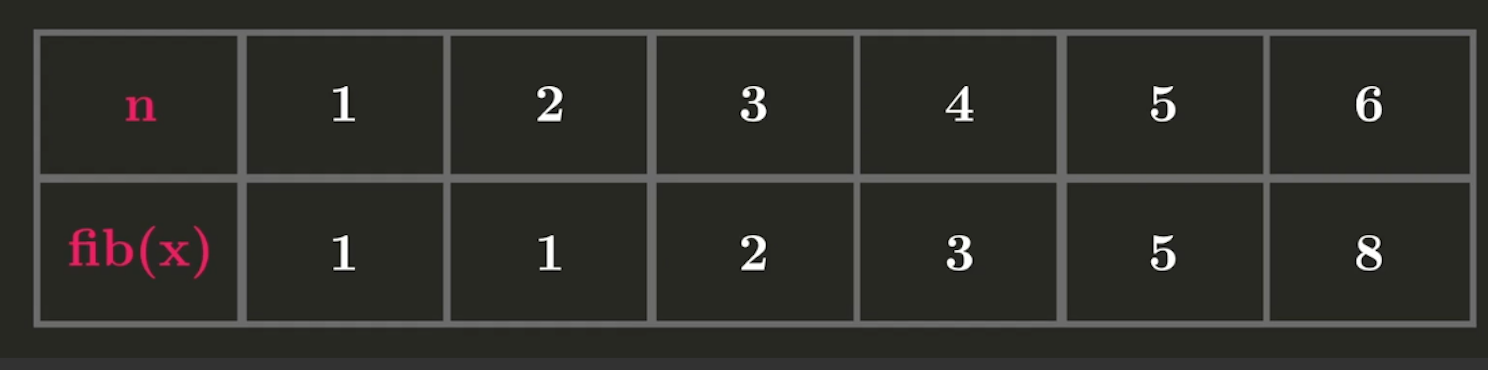
• ver코드잇

    # list로 풀기
    def fib_tab(n):
    		# 이미 계산된 피보나치 수를 담는 리스트
        fib_table = [0, 1, 1]

        # n번째 피보나치 수까지 리스트를 하나씩 채워 나간다
        for i in range(3, n + 1):
            fib_table.append(fib_table[i - 1] + fib_table[i - 2])

        # 피보나치 n번째 수를 리턴한다
        return fib_table[n]

    #test
    fib_tab(10)   #55

    #dictionary로 풀기
    def fib_tab(n):
    	fib_table={}  #피보나치 수가 저장되는 딕셔너리
    	fib_table[1]=1
    	fib_table[2]=1

    	for i in range(3, n+1):
    		fib_table[i]=fib_table[i-2]+fib_table[i-1]

    	return fib_table[n]

    #test
    fib_tab(10)  #55

• ver이코테

# 앞서 계산된 결과 저장을 위한 DP 테이블 초기화(보텀업 방식에서 메모리 저장을 위한 리스트를 DP테이블이라 부름)
d = [0] * 100

# 첫 번째, 두 번째 피보나치 수
d[1] = 1
d[2] = 2
n = 99

# 반복문으로 구현 (보텀업 방식)
for i in range(3, n+1):
    d[i] = d[i-1] + d[i-2]
    
print(d[n])

코드 실행 시 위와 같은 순서로 함수 호출

3. Memoization vs Tabulation , 공간최적화

• Memoization- 재귀사용. 많이 사용하면 스택 오버플로우 가능.. 필요한 연산만 선택적으로 실행
  Tabulation- 반복문 사용. 처음부터 모든 항목을 연산(필요없는 것도 할 수 있음)

• Dynamic Programming 공간최적화
  모든 변수를 저장할 필요가 없는 경우에 , current(현재 값), previoud(이전 값) 두 변수에 값을 저장→사용하는 메모리가 고정되므로 공간복잡도 O(1)임

        def fib_optimized(n):
            current = 1
            previous = 0

            # 반복적으로 위 변수들을 업데이트한다. 
            for i in range(1, n):
                current, previous = current + previous, current

            # n번재 피보나치 수를 리턴한다. 
            return current

- 새꼼달꼼 팔기
    - memoization

      def max_profit_memo(price_list, count, cache):
          # Base Case: 0개 혹은 1개면 부분 문제로 나눌 필요가 없기 때문에 가격을 바로 리턴한다
          if count < 2:
              cache[count] = price_list[count]
              return price_list[count]

          # 이미 계산한 값이면 cache에 저장된 값을 리턴한다
          if count in cache:
              return cache[count]

      		#Recursive Case
          # profit은 count개를 팔아서 가능한 최대 수익을 저장하는 변수
          # 팔려고 하는 총개수에 대한 가격이 price_list에 없으면 일단 0으로 설정
          # 팔려고 하는 총개수에 대한 가격이 price_list에 있으면 일단 그 가격으로 설정
          if count < len(price_list):
              profit = price_list[count]
          else:
              profit = 0

          # count개를 팔 수 있는 조합들을 비교해서, 가능한 최대 수익을 profit에 저장
      		# max_profit_memo()를 재귀적으로 호출
          for i in range(1, count // 2 + 1):
              profit = max(profit, max_profit_memo(price_list, i, cache) 
                       + max_profit_memo(price_list, count - i, cache))

          # 계산된 최대 수익을 cache에 저장
          cache[count] = profit

          return profit

      def max_profit(price_list, count):
          max_profit_cache = {}

          return max_profit_memo(price_list, count, max_profit_cache)

4. Greedy Algorithm

• 그리디 알고리즘

  • 미래를 내다보지 않고 당장의 최적의 선택을 하는 방식
  • 장점:구현이 쉽고 빠름 / 단점: 최적의 답을 보장하지 않음
  • 언제 사용? 최적의 답이 필요하지 않은 경우, 다른 알고리즘이 너무 느릴 경우 등

• 그리디 알고리즘이 최적의 답을 보장하는 조건

  • 최적 부분 구조를 가짐Optiomal Substructure: 부분 문제의 최적의 답으로 기존 문제의 최적의 답을 구할 수 있을 때
  • 탐욕적 선택 속성이 있음Greedy Choice Property:각 단계에서의 탐욕적 선택(당장의 상황에서 목표를 위해 가장 도움이 되는 것)이 최종 답을 구하는 최적의 선택일 때

  ex1. 동전을 거슬려주는 경우. 최적부분구조:가진 동전의 크기로 경우 나누기 가능, 탐욕적 선택 속성: 가장 큰 단위의 돈으로 거슬려주는게 최적의 방식임이 확실

        #최소 동전 거슬려주기
        def min_coin_count(value, coin_list):
        	#누적 동전 개수
        	count = 0;
        	#coin_list를 내림차순으로 정렬해서 반복문을 돌리기
        	for coin in sorted(coin_list, reverse=True):
        		count += value//coin
        		value -= coint*count  #잔액계산. value %= coin으로 쓸 수도 있다
        	return count

   ex2. 08지각벌금 적게 내기

        def min_fee(pages_to_print):
        	sorted_list=sorted(pages_to_print)
        	sum=0
        	result=[]

        	for i in range(len(sorted_list)):
        		sum += sorted_list[i]
        		result.append(sum)

        	return sum(result)