5-1. DFS/BFS 자료구조, 그래프

✓자료구조 - 스택, 큐

탐색(Search)는 '많은 양의 데이터 중에서 원하는 데이터를 찾는 과정'
탐색의 대표 알고리즘은 DFS/BFS.
두 알고리즘을 제대로 이해하려면 기본 자료구조 스택, 큐에 대한 이해가 전제되어야한다!

1. 스택(Stack)

• 선입후출(First In Last Out) - 박스 쌓기 유형
• 파이썬 기본 list자료형의 append, pop메소드 이용

stack=[]

# 삽입(5)-삽입(2)-삽입(3)-삽입(7)-삭제()-삽입(1)-삽입(4)-삭제()
stack.append(5)
stack.append(2)
stack.append(3)
stack.append(7)
stack.pop()
stack.append(1)
stack.append(4)
stack.pop()

print(stack) #최하단 원소부터 출력: [5,2,3,1]
print(stack[::-1] #최상단 원소부터 출력: [1,3,2,5]

2. 큐(Queue)

• 선입선출(First In First Out) - 대기줄 유형
• 파이썬 collection 모듈 deque라이브러리의 append, popleft메소드 사용
  • 일반 list자료형보다 효율성 좋음
  • list(deque객체)로 형변환 가능

from collections import deque

queue = deque()

# 삽입(5)-삽입(2)-삽입(3)-삽입(7)-삭제()-삽입(1)-삽입(4)-삭제()
queue.append(5)
queue.append(2)
queue.append(3)
queue.append(7)
queue.popleft()
queue.append(1)
queue.append(4)
queue.popleft()

print(queue)  #먼저 들어온 순서대로 출력: deque([3,7,1,4])
queue.reverse()
print(queue)  #나중에 들어온 순서대로 출력: deque([4,1,7,3])

3. 재귀 함수(Recursive Function)

• 자기자신을 호출하는 함수
• 주로 dfs에서 사용
• 종료 조건 명시 필수, 내부적으로 스택 자료구조와 동일
• 함수의 점화식(재귀식)을 그대로 소스코드로 옮기므로 간결함.
  • 점화식: 특정한 함수를 자신보다 더 작은 변수에 대한 함수와의 관계료 표현

# (ex) 팩토리얼 구현
def factorial_recursive(n):
    if n<=1:
    	return 1
    return n*factorial_recursive(n-1)

✓그래프 구조

• 그래프 기본 구조: 노드(Node), 간선(Edge), 정점(Vertex)
  • 그래프 탐색: 하나의 노드를 시작으로 다수의 노드를 방문
  • '두 노드가 인접하다' : 두 노드가 간서으로 연결되어 있음
• 인접 행렬(Adjacency Matrix)
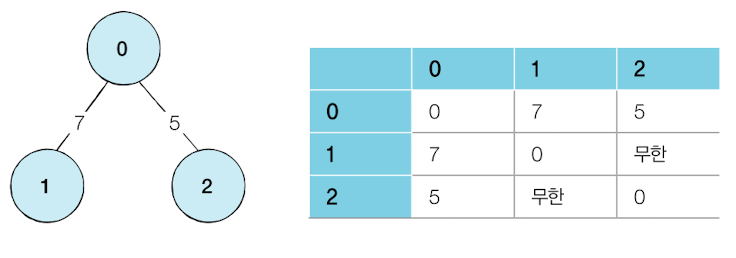
  • 2차원 배열로 그랴프의 연결 방식 표현
    

INF = 999999999 #무한의 값으로 초기화

graph = [
  [0,7,5],
  [7,0,INF],
  [5,INF,0]
]

print(grapgh)  #[[0,5,6],[7,0,999999999],[5,999999999,0]]

• 인접 리스트(Adjacency List)
  • 리스트로 그래프 연결 관계 표현
  • 자신과 연결되 노드와의 관계만 표현
    

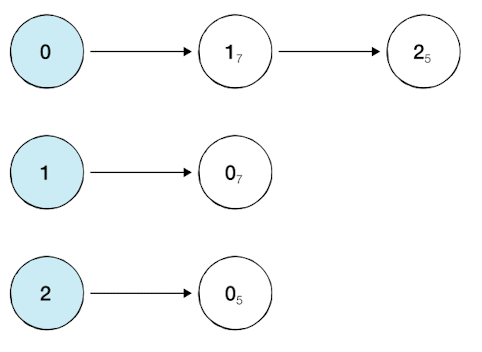
#행(Row)가 3개인 2차원 리스트로 인접 리스트 표현
graph = [[] for _ in range(3)]

#노드 0에 연결된 노드 정보 저장(노드,거리)
graph[0].append((1,7))
graph[0].append((2,5))

#노드 1에 연결된 노드 정보 저장(노드,거리)
graph[1].append((0,7))

#노드 2에 연결된 노드 정보 저장(노드,거리)
graph[2].append((0,5))

print(grapgh)  #[[(1,7),(2,5)],[(0,7)],[(0,5)]]

• 인접 행렬, 인접 리스트 비교
  • 메모리: 인접 리스트 better (메모리 공간 낭비 적음)
  • 속도: 인접 행렬 better