Sort - 정렬
Selection Sort (선택 정렬)
- 가장 작은 값을 선택해서 앞으로 보내는 정렬 방법
예시.
mix된 1~10까지의 수를 정렬
1 6 2 8 3 4 9 5 7 10 -> 1 2 3 4 5 6 7 8 9 10
시간복잡도는
10 + 9 + 8 + ... + 1
10 (10 + 1) / 2 = 55
N (N + 1) / 2 # 컴퓨터에서는 N이 굉장히 클 수 있으니 2로 나눈 값이나, 1을 더한 값은 없앰
N * N
O(N^2) # Big O 표기법 -> 알고리즘의 총 연산 횟수.
N^2는 알고리즘에서 굉장히 비효율적인 방법
Bubble Sort (버블 정렬)
-
가까지에 있는 두 숫자끼리 비교해서 당장 더 작은 숫자를 앞으로 보내주는 방법
-
즉, 옆에 있는 값과 비교하여 더 작은 값을 반복적으로 앞으로 보내는 정렬 방법
-
결과적으로 한 싸이클이 돌면 가장 큰 값이 맨 오른쪽으로 이동 (정렬될 때까지 반복)
-
시간 복잡도 : O(N^2)
-
굉장히 비효율적임.
Insertion Sort (삽입 정렬)
- 각 숫자를 적절한 위치에 삽입하는 방법
- 필요할 때만 위치를 바꿀 수 있음.
예시.
1 6 2 8 3 4 9 5 7 10
이 상태에서 6이 들어갈 수 있는 곳은
1 6 2 8 3 4 9 5 7 10
이 두군대임. (1보다 크기 때문에 오른쪽으로 Insert)
1 6 2 8 3 4 9 5 7 10
이후에 2가 들어갈 수 있는 곳은
1 6 2 8 3 4 9 5 7 10
이 세군대임. (1보다 크고 6보다 작기 때문에, 두 번째 에 들어감)
1 2 6 8 3 4 9 5 7 10
...
1 2 3 4 5 6 7 8 9 10
이렇게 다 정렬 될 때까지 반복
- 시간 복잡도 : O(N^2)
Quick Sort (퀵 정렬)
-
하나의 큰 문제를 두 개의 작은 문제로 분할하는 방법 (원소를 두 개로 나눔. pivot값 설정)
-
즉, 특정한 기준으로 큰 숫자와 작은 숫자를 서로 교환한 뒤에 배열을 반으로 나눔.
-
시간 복잡도 : O(N * logN) # 위에 있는다른 Sort와 비교했을 때 굉장히 빠른편. 왼쪽과 오른쪽을 나눠서 정렬하기 때문
-
다만, 최악의 경우 O(N^2)의 시간복잡도가 나올 수 있음.
Merge Sort (병합 정렬)
-
하나의 문제를 정확히 반으로 나누고 나중에 정렬하는 방법
-
너비 = N , 높이 = logN
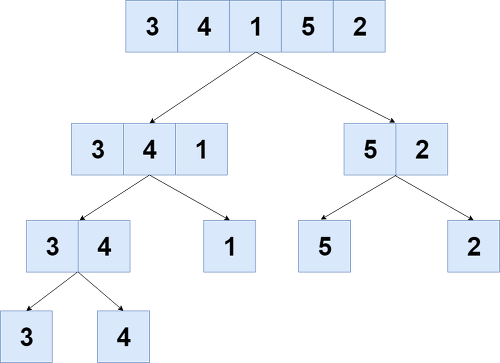
-
합치는 순간에 정렬 (i-왼쪽 데이터, j-오른쪽데이터, k-새로운배열 사용)
-
시간 복잡도 : O(N * logN)
-
다만, 기존의 데이터를 담을 추가적인 배열 공간이 필요하기 때문에, 메모리 활용이 비효율적
-
일반적으로 quick sort보다 느리지만, 어떠한 상황에도 O(N * logN)을 보장
Heap Sort (힙 정렬)
https://blog.naver.com/ndb796/221228342808 - 참고
-
힙(Heap) 자료구조(완전 이진 트리)를 활용한 정렬 방법.
-
최대 힙(Max Heap)을 구성해 가장 큰 값을 루트로 만든 후, 이를 배열 끝으로 보내고 힙을 재구성하여 정렬.
-
힙 구성 및 정렬 과정에서 반복적으로 루트와 마지막 원소를 교환하고 힙을 재정렬함.
-
완전 이진 트리 -> 데이터가 root 노드부터 시작해서 왼쪽, 오른쪽 자식 노드에 데이터를 다 채우는 것
-
힙 -> 부모 노드가 자식 노드보다 큰 경우
-
자식 노드가 더 큰 경우, 부모 노드와 위치를 바꿔야 함. (이를 Heapify Algorithm 이라 부름)
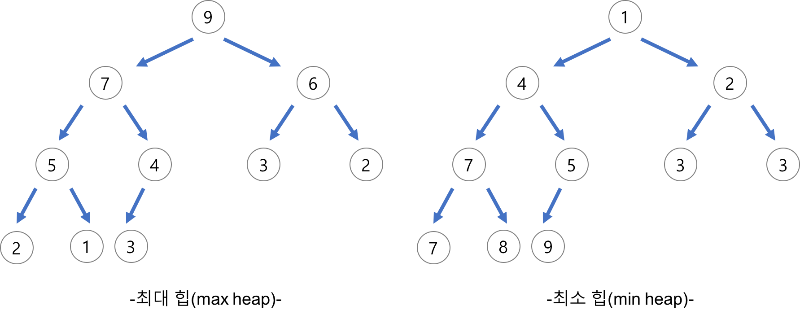
- 시간 복잡도 : O(N * logN)
Counting Sort (계수 정렬)
- 데이터의 '범위를 기반'으로 정렬하는 방법.
- 다른 정렬은 위치를 바꾸어 가며 정렬을 하였지만, 계수 정렬은 크기를 기준으로 하기 때문에 위치를 바꿀 필요가 없음.
- 배열의 각 요소가 등장한 빈도수를 세어, 누적합을 이용해 정렬된 위치에 배치.
- 음수가 없는 정수나 범위가 제한된 데이터에서 빠르게 동작함.
예시.
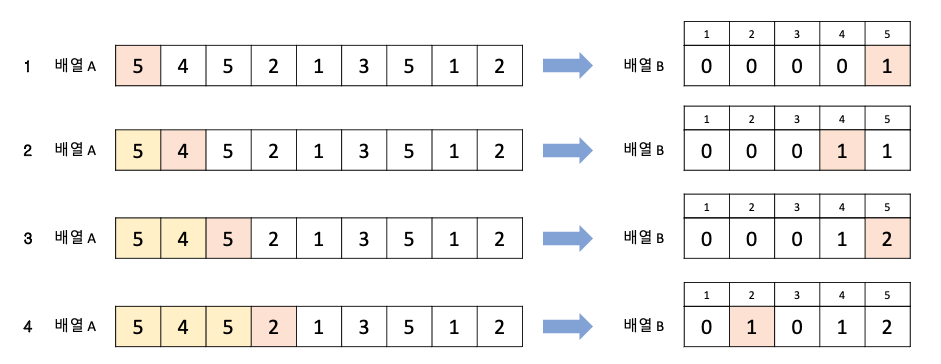
- 사진과 같이, 크기를 알면, 각 크기에 맞게 해당되는 데이터의 숫자를 업데이트
- 업데이트를 완료하고 나면, 배열B에 저장되어 있는 값을 차례대로 출력
- 1 = 2번 출력, 2 = 2번 출력, 3 = 1번 출력, 4 = 1번 출력, 5 = 3번 출력
- 시간 복잡도 : O(N)
