백준 17087, 9613 문제 풀이

1. 오늘의 알고리즘 문제

1. 숨바꼭질6

public class p17087 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;
        String str1 = br.readLine();

        st = new StringTokenizer(str1, " ");

        int n = Integer.parseInt(st.nextToken());  //동생의 수
        int s = Integer.parseInt(st.nextToken());  //출발 지점

        String str2 = br.readLine();
        st = new StringTokenizer(str2, " ");

        int[] array = new int[n + 1];     //1개만 있을때 x 를 만들지 못하므로 +1 해주었음

        for (int i = 0; i < n; i++) {
            array[i] = Math.abs(Integer.parseInt(st.nextToken()) - s);
        }

        int x = gcd(array[0], array[1]);  // for문을 돌며 값을 하나씩 넣어주기 위해 초기값을 생성함

        for (int i = 2; i < n; i++) {
            x = gcd(array[i], x);
        }
        System.out.println(x);
    }

    public static int gcd(int a, int b) {
        while (!(b == 0)) {
            int r = a % b;
            a = b;
            b = r;
        }
        return a;
    }
}

//분류: 숨바꼭질6 (수학)
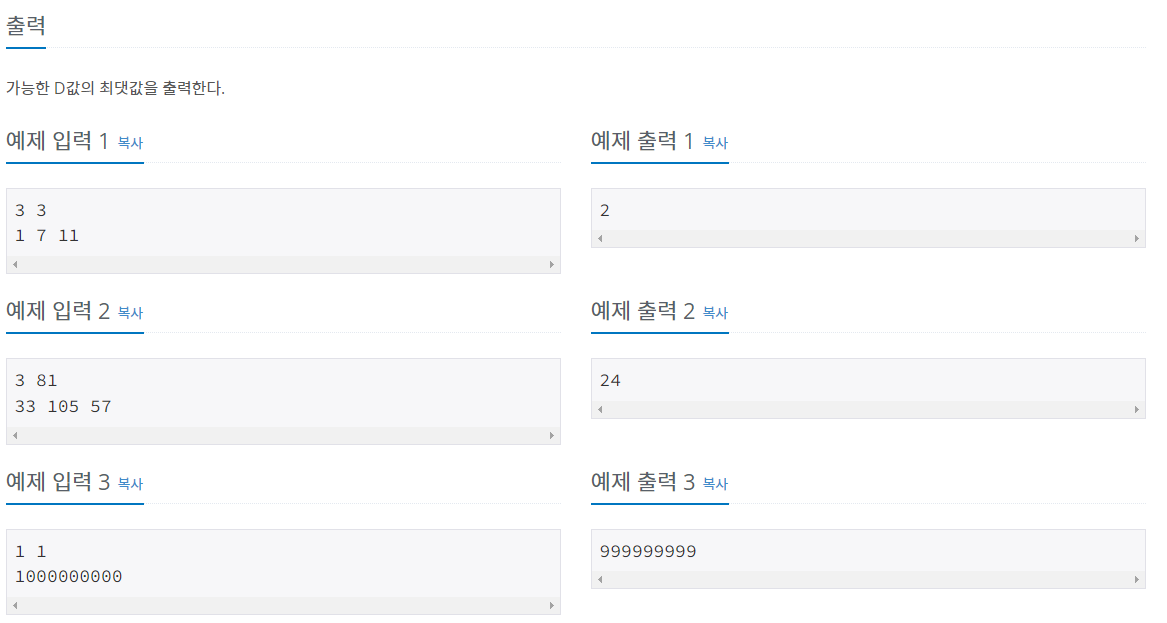
//알고리즘 : N명의 동생과 숨바꼭질을 하고 수빈이의 현재 위치가 S 일때 수빈이는 +D , -D 만큼만 움직일 수 있음. 모든 동생에게 가기 위한 가장 큰 수 D 를 찾는 문제이다.
//이 문제를 풀기 위해서는 모든 동생들과 수빈이의 거리 차이를 구한 뒤, 모든 거리차이 들의 최대 공약수를 구하게 되면 모든 동생에게 갈 수 있게 된다.
//또한 gcd(array3,gcd(array[2],gcd(array[0],array[1]))) 이런 식으로 2개가 아닌 여러개의 숫자들의 최대 공약수를 구할 수 있다.
//배운점 : 수빈이의 위치 와 동생들의 거리 차이를 절대값으로 나타내야 하는 경우가 있는데 이때 Math.abs 를 사용하여 절댓값 구하는 것을 다시 한번 상기시키게 되었고,
//또한 위에 적은 것 처럼 gcd 값을 구하면 그 값이 또 다른 gcd의 파라미터로 들어가기 때문에 for 문을 짜면서 고민을 많이 하게 되었는데  int x = gcd(array[0], array[1]);
//를 만들어 주고 for문을 돌려 하나씩 넣어 주는 방식으로 해결하게 되었다.

2. GCD의 합

public class p9613 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringBuilder sb = new StringBuilder();
        StringTokenizer st;


        int t = Integer.parseInt(br.readLine());


        while(t-- > 0){
            String str = br.readLine();
            st = new StringTokenizer(str," ");

            int n = Integer.parseInt(st.nextToken());
            long result =0;

            int[] array = new int[n];
            for(int i=0; i <n; i++){
                array[i] = Integer.parseInt(st.nextToken());
            }

            for(int i=0; i<n-1; i++){
                for(int j=i+1; j<n; j++){
                    result += gcd(array[i],array[j]);
                }
            }
            sb.append(result + "\n");
        }
        System.out.println(sb);
    }

    public static int gcd(int a, int b) {
        while (b != 0) {
            int r = a % b;
            a = b;
            b = r;
        }
        return a;
    }
}


//분류 : GCD합 (수학)
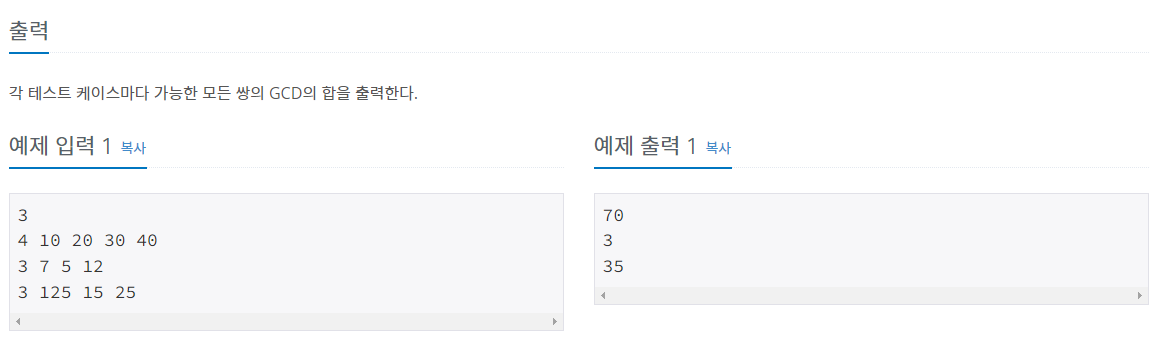
//알고리즘 : 테스트케이스 t 를 받고 수의 개수 n 을 받아서 각 테스트 케이스마다 가능한 모든 쌍의 GCD 합을 출력해야 한다. GCD 알고리즘은 유클리드 호제법을 통해
// static 메소드로 구현을 했고 r = a % b , a = b , b = r 을 해주고 a 값을 리턴해주면 최대공약수 값이 리턴된다.(이때 a와 b 의 크기는 신경쓰지 않아도 된다)
// 그 뒤에 2중 for문을 통해서 가능한 모든 쌍의 GCD 값을 result 에 더해준다.
//배운점 : 처음에 답이 틀렸다고 나와서 왜그런가 봤더니 result 를 처음에는 int 형으로 선언해주었다고 long 형으로 바꿔주니 답이 맞게 되었다.
//저번에도 이와 비슷하게 int 형에서 값을 다 못담는 경우가 있었는데 좀 큰 수가 나올거 같다 싶으면 long 형으로 선언해주면 졸을 것 같다.