알고리즘 1) DFS

1) 인접 행렬과 인접 리스트

프로그래밍에서 그래프는 크게 2가지 방법으로 표현할 수 있다.

1. 인접 행렬 : 2차원 배열로 그래프의 연결 관계를 표현하는 방식

2차원 배열에 각 노드가 연결된 형태를 기록하는 방식으로 파이썬에서는 2차원 리스트로 구현한다

INF = 9999999999

# 2차원 리스트를 이용해 인접 행렬 표현
graph = [
    [0, 7, 5],
    [7, 0, INF],
    [5, INF, 0]
]

print(graph)

출력 : [[0, 7, 5],[7, 0, 9999999999],[5, 9999999999, 0]]

2. 인접 리스트 : 리스트로 그래프의 연결 관계를 표현하는 방식

모든 노드에 연결된 노드에 대한 정보를 차례대로 연결하여 저장하는 방식으로 파이썬에서는 2차원 리스트로 구현한다

# 행이 3개인 2차원 리스트로 인접 리스트 표현
graph = [[] for _ in range(3)]

# 노드 0에 연결된 노드 정보 저장(노드, 거리)
graph[0].append((1, 7))
graph[0].append((2, 5))

# 노드 1에 연결된 노드 정보 저장(노드, 거리)
graph[1].append((0, 7))

# 노드 2에 연결된 노드 정보 저장(노드, 거리)
graph[2].append((0, 5))

print(graph)

출력 : [[(1, 7), (2, 5)],[(0, 7)],[(0, 5)]]

3. 인접 행렬 vs 인접 리스트 비교
두 방식은 어떤 차이가 있을까?
1) 메모리 측면
-인접 행렬은 모든 관계를 저장해 노드 개수가 많을수록 메모리가 불필요하게 낭비된다.
-인접 리스트는 연결된 정보만을 저장하기 때문에 메모리를 효율적으로 사용한다.
2) 시간 측면
-인접 행렬은 두 노드가 연결되어 있는지에 대한 정보를 얻는 속도가 빠르다.
-인접 리스트는 연결된 데이터를 하나씩 확인해야 하기 때문에 두 노드가 연결되어 있는지에 대한 정보를 얻는 속도가 느리다.

2) DFS(Depth-First Search) 알고리즘

• DFS는 깊이 우선 탐색이라고도 부르며 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘
• 코딩 테스트에서 대부분의 그래프 탐색은 DFS로 구현하게 된다.
• DFS는 스택 자료구조(혹은 재귀 함수)를 이용하며, 구체적인 동작은 아래와 같다.

1. 탐색 시작 노드를 스택에 삽입하고 방문 처리를 한다.
2. 스택의 최상단 노드에 방문하지 않은 인접한 노드가 하나라도 있으면 그 노드를 스택에 넣고 방문 처리한다. 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼낸다.
3. 더 이상 2번의 과정을 수행할 수 없을 때까지 반복한다.

step 1. 아래와 같은 그래프가 있다고 하자

step 2. 1을 방문

step 3. 1과 인접한 2를 방문

step 4. 2와 인접한 4를 방문

step 5. 4와 인접한 8을 방문

step 6. 더 이상 인접한 노드가 없으므로 인접한 노드가 생길 때까지 스택에서 뺀다

step 7. 2와 인접한 노드 중 방문하지 않은 5를 방문

step 8. 5와 인접한 9를 방문

step 9. 더 이상 인접한 노드가 없으므로 인접한 노드가 생길 때까지 스택에서 뺀다

step 10. 1과 인접한 노드 중 방문하지 않은 3을 방문

step 11. 3과 인접한 6을 방문

step 12. 더 이상 인접한 노드가 없으므로 인접한 노드가 생길 때까지 스택에서 뺀다

step 13. 3과 인접한 노드 중 방문하지 않은 7을 방문

step 14. 완성

def dfs(graph, v, visited):
    # 현재 노드를 방문 처리
    visited[v] = True
    print(v, end=' ')
    # 현재 노드와 연결된 다른 노드를 재귀적으로 방문
    for i in graph[v]:
        if not visited[i]:
            dfs(graph, i, visited)
 
# 각 노드가 연결된 정보를 표현
graph = [
    [],  # 0번 노드가 없으므로 index 0은 비워둠
    [2, 3],  # 1번 노드와 연결된 노드
    [1, 4, 5],
    [1, 6, 7],
    [2, 8],
    [2, 9],
    [3],
    [3],
    [4],
    [5]
]
 
# 각 노드가 방문된 정보를 표현
visited = [False]*10
 
dfs(graph, 1, visited)

출력 : 1 2 4 8 5 9 3 6 7

Outro

DFS는 탐색 알고리즘으로 그래프 그림을 이용한다.
1차원 배열이나 2차원 배열을 그래프 형태로 생각하면 DFS를 이용해 문제를 수월하게 풀 수 있다. (cj 2번 문제..ㅠㅠ)

예를 들어 게임 맵이 3x3 형태의 2차원 배열이고 각 데이터를 좌표라고 생각해보자. 이때 각 좌표를 상하좌우로만 이동할 수 있다면 모든 좌표의 형태를 다음처럼 그래프의 형태로 바꿔서 생각할 수 있다.

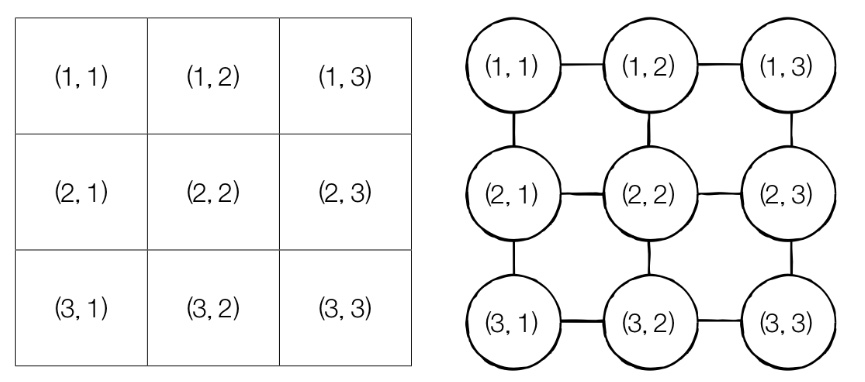
코딩 테스트 중 2차원 배열에서의 탐색 문제를 만나면 이렇게 그래프 형태로 바꿔서 생각하면 풀이 방법을 조금 더 쉽게 떠올릴 수 있다.