그리디
- 그리디는 매 순간 가장 좋아보이는 것을 선택하는 알고리즘이다.
- 현재의 선택이 나중에 미칠 영향에 대해서는 고려하지 않아 매 순간 좋은 것을 선택한다 해서 최종적으로 좋은 것을 선택하는 것은 아니다.
- 그리디 알고리즘 문제는 기준에 따라 좋은 것을 선택하는 알고리즘이므로 문제에서 '가장 큰 순서대로', '가장 작은 순서대로'와 같은 기준을 알게 모르게 제시해주며, 이런 경우 정렬을 사용해야 하므로 그리디 알고리즘 문제는 자주 정렬 알고리즘과 짝을 이뤄 출제된다.
1) 그리디 알고리즘 예시 - 거스름돈
문제
카운터에는 거스름돈으로 사용할 500원, 100원, 50원, 10원짜리 동전이 무한히 존재한다고 가정한다. 손님에게 거슬러 줘야 할 돈이 N원일 대 거슬러줘야 할 동전의 최소 갯수를 구하라. (단, 거슬러줄 돈 N은 항상 10의 배수이다.)
문제 해설
이 문제를 그리디 알고리즘을 이용해서 푼다면 가장 큰 화폐 단위부터 돈을 거슬러 주면 된다. N원을 거슬러줄 때 가장 먼저 500원으로 거슬러줄 수 있는 만큼 거슬러주고 그 다음 100원, 50원, 10원 순서대로 거슬러줄 수 있는 만큼 거슬러주면 최소의 동전 갯수로 모두 거슬러줄 수 있다.
문제 풀이
n = 1260
count = 0
# 큰 단위의 화폐부터 차례로 확인
coin = [500, 100, 50, 10]
for i in coin:
count += n // i
n %= i
print(count)거스름돈 문제에서 그리디 알고리즘의 정당성
그리디 알고리즘으로 문제의 해법을 찾았을 때는 그 해법이 정당한지 검토해야 한다. 거스름돈 문제는 가지고 있는 동전 중 큰 단위가 항상 작은 단위의 배수이므로 작은 단위의 동전들을 종합해 다른 해가 나올 수 없기 때문에 그리디 알고리즘으로 최적의 해를 구할 수 있다.
만약 800원을 거슬러줘야 하는데 화폐 단위가 500원, 400원, 100원인 경우 그리디 알고리즘으로는 4개의 동전(500원+100원×3)을 거슬러줘야 하지만 이 경우 최적의 해는 2개의 동전(400원×2)을 거슬러주는 것이다.
따라서 그리디 알고리즘을 이용해 문제를 해결할 때는 그리디 알고리즘이 항상 최적의 해를 구할 수 있는지 정당성을 검토해봐야 한다.
2) 그리디 알고리즘과 다이나믹 프로그래밍의 비교
- 그리디 알고리즘과 다이나믹 프로그래밍은 최적 부분 구조 문제를 푼다는 점에서 유사하다.
- 둘의 차이점은 아래와 같다.
- 그리디 알고리즘은 각 단계마다 로컬 최적해를 찾으며 문제를 작게 줄여나간다.
- 다이나믹 프로그래밍은 하위 문제에 대한 최적의 솔루션을 찾은 다음, 이 결과들을 결합한 정보에 입각해 전역 최적 솔루션을에 대한 선택을 한다.
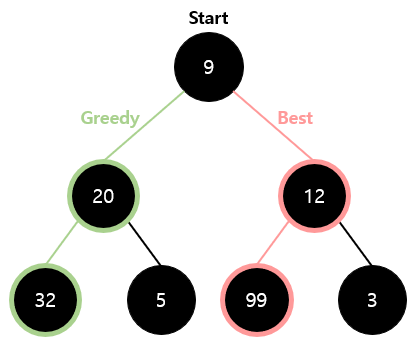
- 위 그림에서 각 단계마다 로컬 최적해를 선택하는 그리디 알고리즘으로 풀이했을 때는 9+20+32=61이다.
- 위 그림에서 최적의 솔루션을 찾은 다음, 최적의 솔루션에 대한 정보에 입각해 전역 최적 솔루션을 선택하는 다이나믹 프로그래밍으로 풀이했을 때는 9+12+99=120이다.
