컴퓨터에서 실수를 표현하는 방식

컴퓨터에서 실수를 표현하는 방식에는 두 가지 방식이 있다.
바로 고정 소수점 방식과 부동 소수점 방식이다.

고정 소수점

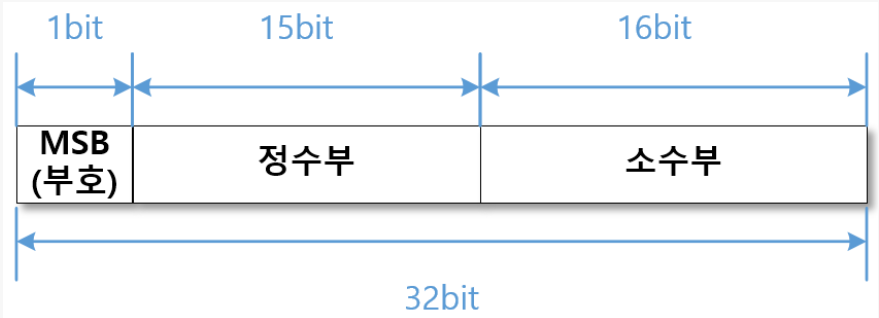
• 정수를 표현하는 비트 수(15비트)와 소수점 이하를 나타내는 비트 수(16비트)를 고정해둔다
• 정수를 표현하는 비트가 크기 때문에 큰 수를 나타낼 수는 있으나, 소수점 이하를 나타내는 비트가 고정돼있어 소수점 이하를 정밀하게 나타내기는 어렵기에 소수점 이하의 비트 수를 고정하지 않는 부동 소수점이라는 대안이 있다.

부동 소수점

• 부동 소수점은 말 그대로 소수점이 둥둥 떠 다닌다는 의미를 가지고있다. 소수점을 고정하지 않기에 수를 더 정밀하게 나타낼 수 있다.
• 부동소수점은 Floating Point를 줄여 FP라고 부르기도한다.

부동 소수점 표현 방식

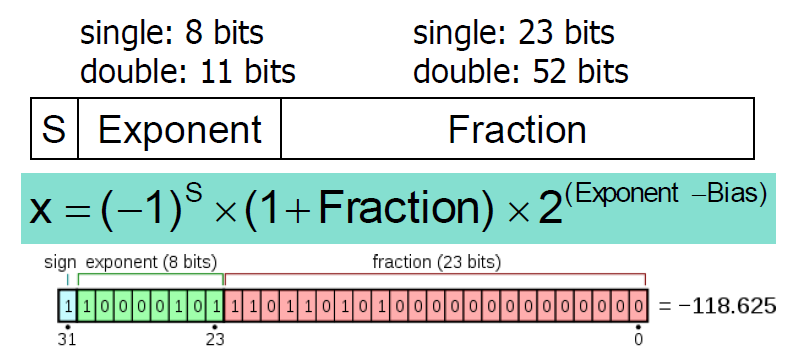
• 부동 소수점을 표시하는 형태를 정의한 표준을 IEEE Std 754-1985라고 한다.

• S : 부호를 표시하는 sign bit이며 0이면 양수, 1이면 음수이다

• Exponent : 지수부를 의미한다, actual exponent는 Bias값을 빼주어야한다

  • Bias : Bias는 8비트 single에서는 127, 11비트 double에서는 1023이다. 8비트의 actual exponent값이 -127 ~ 127이므로 bias를 127로 정하고 exponent에 더하면 0이나 양수가 된다. exponent필드에 저장될 값을 이렇게 만드는 이유는 아래서 설명할 것이다.

• Fraction : 가수부를 의미한다 여기서 1을 더해주는 이유는 어떤 이진수든 1을 포함하고 있기 때문에 부동 소수점의 format의 통일성을 주는 것이다

• Significand : 여기서 (1 + Fraction) 을 Significand라고 한다

• 부동 소수점을 표시하는 방법에는 Single Precision과 Double Precision이 있다. 위 그림은 Single Precision의 예시 사진이다.

• Single Precision

  • 총 32비트의 크기를 가지며 MSB는 부호비트, 그 다음 8비트는 지수부(Exponent), 그 다음 23비트는 가수부(Fraction)라고 부른다
  • C언어의 float 자료형에 해당한다

• Double Precision

  • 총 64비트의 크기를 가지며 MSB는 부호비트, 그 다음 11비트는 지수부(Exponent), 그 다음 52비트는 가수부(Fraction)라고 부른다
  • C언어의 double 자료형에 해당한다

• 즉, Double Precision이 Single precision보다는 수를 더 세밀하게 나타낼 수 있다.

Bias의 존재와 이유

• actual Exponent값에 bias값을 더해주어 signed로 표현해야 더 작은수까지 나타낼 수 있다

• 비교와 정렬의 복잡도가 낮아진다

  • 부동 소수점을 표시할 때는 (1+Fration) * 2^(Exponent - Bias)로 표기한다. 그래서 두 수를 비교할 때는 Exponent 먼저 비교한다. 위의 예제는 single precision의 예제이다. Exponent값인 -1과 1을 비교하려면 뺄셈 연산을 해주어 0보다 큰지 확인해야한다. 그런데 만약 두 수가 모두 unsigned라면? 8자리의 비트를 MSB부터 차례로 비교해주면된다.

Exponent Filed에 저장되는 값과 actual Exponent 값은 다름을 주의해야한다.
Exponent Field = actual Exponent + Bias
actual Exponent = Exponent Field - Bias
여기서 Bias값은 Single Precision에서는 127, Double Precision에서는 1023이다.

부동소수점의 범위

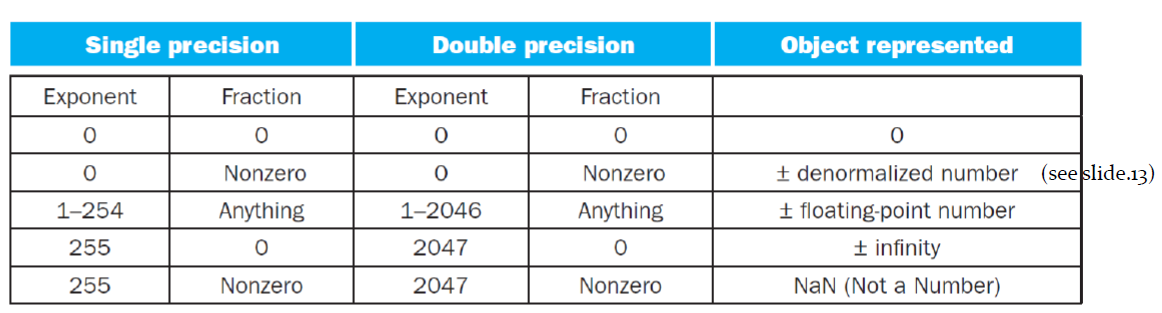
Single Precision

예약값은 Exponent Field가 0일 때와 255일 때이고, 특정 표현으로 표기하기로 약속돼있다. 최솟값은 Exponent Field가 1일 때, 최댓값은 Exponent Field가 254일 때이다.

Double Precision

Single Precision과 똑같은 매커니즘으로 구할 수 있다.

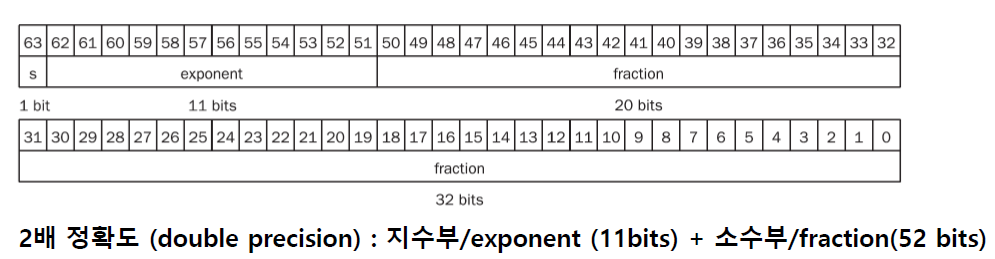
double precision은 메모리에 다음과 같이 저장이 된다.
1비트의 sign bit와 11비트의 exponent, 52 비트의 fraction으로 저장이 되는데, 32비트의 word 단위로 쪼개서 저장을 한다.

부동 소수점 변환 예제

10진수 -> 부동소수점

• 10진수를 2진수로 바꾼다
• FP의 정규 표현식으로 표현한다
• 부호를 확인해 sign bit를 구한다
• Fraction을 구한다
• actual Exponent + Bias = Exponent Field 값을 구해준다
• MSB부터 이어붙여준다

부동소수점 -> 10진수

각 비트 값을 보고 정규식으로 변환, 다시 10진수로 변환한다

Underflow와 Overflow 처리

가끔 우리가 예상했던 것보다 결과 값이 매우 작게 나오는 경우도 있다.
예를 들어, Single Precision에서 A x 2^127과 B x 2^3을 곱해준다.
그러면 결과는 A x B x 2^130으로, 8비트만 사용하는 Exponent Field가 overflow가 나게 된다.
1 0000 0010 에서 MSB인 1이 사라지고 0000 0010으로 나타나게된다. 따라서 Signed로 표시하면 -125의 결과 값이 나온다.
이런 경우 우리는 Single -> Double Precision으로 format을 바꿔주면 이러한 overflow나 underflow 현상을 예방할 수 있다.

C언어에서는 float -> double로 형변환을 해주곤한다.

Denormal Number

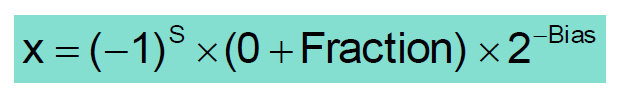
절댓값의 크기가 아주 작은 수를 표현할 때를 위해 사용한다.
Fraction에 더해주던 hidden bit를 1이 아닌 0으로 해준다
denormal number를 사용해주면 0과 1사이의 숫자 두 개를 곱할수록 숫자가 0에 수렴해 underflow에 가까워지는 경우를 막아줄 수 있다

부동 소수점 덧셈

• Exponent가 더 큰 것을 기준으로 삼아 지수부를 통일하고, 그에 따라 소수점을 정렬한다
• significand를 더해준다
• 식을 정규화해주고, under/overflow를 체크한다
• 요구되는 유효 숫자에 따라 반올림을하고 다시 정규화해준다

부동 소수점 덧셈 연산기

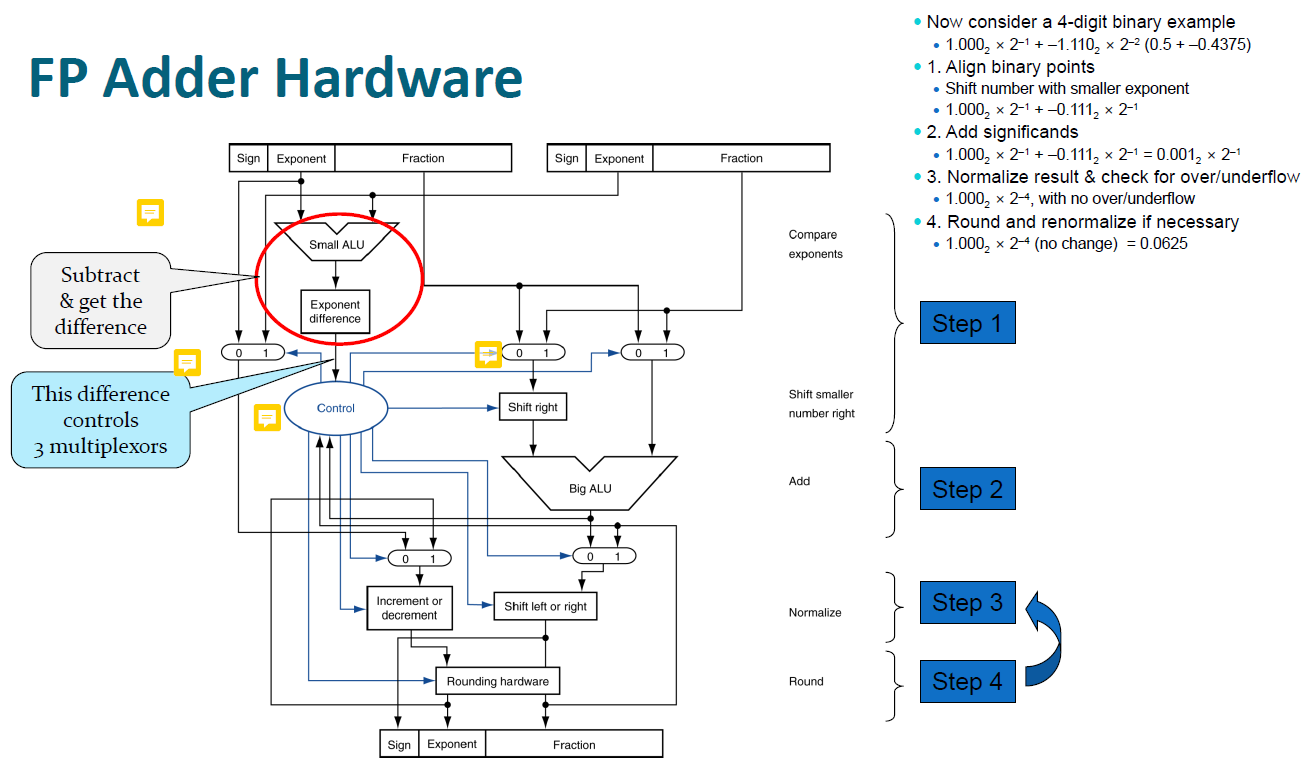
위에서 부동 소수점의 덧셈 연산을 해주었는데, 이 연산기를 어떻게 구현할지 보자. 위 그림 오른쪽 상단의 예제에서 -0.5를 A, -0.4375를 B라고하자.

step1

• 소수점 정렬 시, 두 exponent중 더 큰 것을 기준으로 잡아야하므로 exponent의 뺄셈 연산을 해야돼서 뺄셈 연산기가 들어간다.
• 위 그림에서 뺄셈기 아래 라인에 있는 3개의 mux가 정렬을 돕는다.
  • 맨 왼쪽 mux는 기준이 되는 exponent를 select한다(A의 exponent인 -1 select)
  • 가운데 mux는 소수점 위치 보정이 필요한 significand를 선택한다(B의 significand를 선택)
  • 맨 오른쪽 mux는 소수점 보정이 필요하지 않은 significand를 선택한다(A의 significand를 선택)
  • 그리고 Control은 몇 칸을 shift right해야되는지와 위의 mux에서 필요한 신호들을 보낸다

step2

• 정렬이 끝난 두 FP의 significand를 더한다

step3

• 정규화한다

step4

• 올림한다

부동 소수점 곱셈

부동 소수점의 곱셈은 덧셈보다 더 쉽다
왜냐하면 exponent를 맞춰 줄 필요가 없고, 그에 따른 significand를 정렬해줄 필요가 없기 때문이다.

• exponent를 더해준다
  • 여기서 두 FP의 actual exponent에서 bias를 빼주는 것이 아닌, exponent field에 저장되는 값에서 bias를 빼주면된다
• significand를 곱해준다
• 결과를 정규화 & over/underflow를 체크한다
• 필요하다면 올림을 해준다
• 부호 비트를 정해준다

부동 소수점 연산기의 복잡성

• Floating Point 곱셈 연산기는 FP 덧셈 연산기와 복잡도가 똑같지만, 덧셈기에는 덧셈기가 들어가고, 곱셈기에는 곱셈기가 들어간다.
• FP 연산기는 덧셈, 뺄셈, 곱셈, 나눗셈, 역수 계산, 제곱근 계산등의 다양한 연산을 수행하며, FP를 정수로 변환하는 연산도 지원한다.
• 정수 연산에 비해 부동소수점 연산은 이러한 복잡한 연산들 때문에 한 사이클에는 연산을 다하기는 힘들고 여러 사이클에 거쳐 연산이 이루어져야한다.
• 따라서 pipeline이 필요하다(ch4)

LEGv8에서의 부동 소수점 instruction

• LEGv8에서는 Integer을 저장하는 레지스터와 FP를 저장하는 레지스터가 따로 존재한다
  • integer는 흔히 X0~X31 레지스터에, single precision을 S0~S31, double precision을 D0~D31이라는 레지스터에 저장한다
  • 이렇게 정수와 FP를 따로 저장하면 코드의 복잡도를 낮출 수 있다
• 공간의 효율성을 위해 D 레지스터의 오른쪽 32비트에는 S 레지스터의 값을 저장한다

다음과 같이 FP에 대한 연산이면, 접두사로는 Floating을 의미하는 F가, 접미사로는 S(Single)와 D(Double)가 붙는다.

FP 연산의 정확성 높이기

IEEE Std 754에서는 FP 연산시 유효숫자 이외에는 반올림을 하는데, 만약 유효숫자가 3자리라면 3자리로 절삭을 해버리고 연산을 하는게 아니고, 뒤에 두 비트 정도를 extra bit로 남긴 후 연산을 하고 반올림을 해 연산의 정확성을 높인다.

이에 따르면 extra bit를 반올림시 0~49이면 내림이 되고 50~99이면 올림이 된다.

대신 이렇게 연산을 세부화하면 연산의 정확성은 좋아지나, 하드웨어 cost가 들고 복잡도가 더 늘어난다.

그래서 하드웨어 설계 시 trade off가 있으므로 이를 고려하고 필요에 따라 연산의 방식을 설계하면 된다.

SIMD

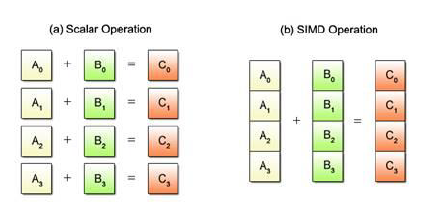
이미지 처리나 뉴럴 네트워크 연산에서는 FP 연산이 필요한 경우가 많다.
그래서 128비트를 여러 개로 쪼개서 여러 개의 데이터를 넣고 각각의 데이터를 벡터로 취급해 한 번의 연산에 여러 개의 데이터를 처리하는 SIMD라는 아키텍처가 존재한다.

ARMv8 SIMD instructions

ARMv8에서는 SIMD 아키텍처에 기반한 연산을 다음의 명령어로 지원한다.

• 레지스터는 V라는 레지스터를 사용한다

• V1.16B라고 하면 128비트를 Byte단위로 16개의 벡터로 쪼개어 계산을 한다.
  총 16개의 데이터를 한 번에 연산할 수 있다

• V1.4S면, 128비트를 Single precision(32비트) 단위로 4개의 벡터로 쪼개어 계산을 한다
  총 4개의 데이터를 한 번에 연산할 수 있다