최근접 점의 쌍 찾기

Song_MinGyu·2022년 4월 9일

algorithm 분할정복

Algorithm

목록 보기

11/30

문제

최근접 점의 쌍을 찾는 문제는 2차원 평면상의 n개의 점이 입력으로 주어질 때, 거리가 가장 가까운 한 쌍의 점을 찾는 문제.

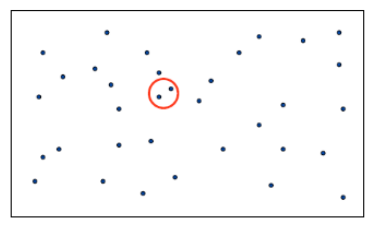
간단한 해결 방법

모던 점에 대하여 각각의 두 점 사이를 계산하여 가장 가까운 점을 찾는 방법
$_nC_2$ 가 소요 => 모든 순서를 조합해야하므로 $O(n^2)$ 이 소요된다.
따라서 해당 방법은 시간이 꽤 오래 걸리므로 다른 방법을 찾아야 한다.

효율적인 해결 방법

분할 정복을 이용한다.
- n개의 점을 절반으로 분할하여 각각의 부분 문제에서 최근접 점의 쌍을 찾고 2개의 부분 해 중에서 짧은 거리를 가진 점의 쌍을 일단 찾는다.

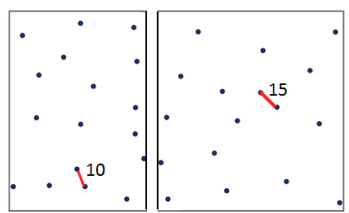
하지만 분할 하면서 생기는 중간 영역에 대한 최단 거리를 따로 고려하는 방법 또한 사용해야한다.

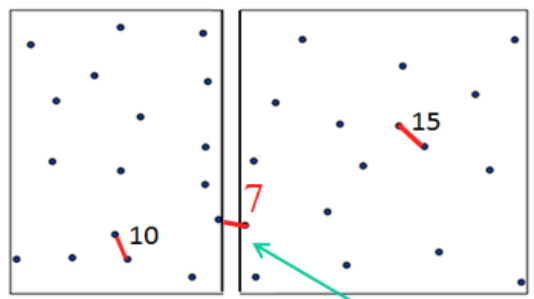
중간 영역 탐색 방법

$d=min(왼쪽최근접점쌍의거리,오른쪽최근접점쌍의거리)$
배열에는 점들이 x-좌표의 오름차순으로 정렬되어있고 y좌표는 생략

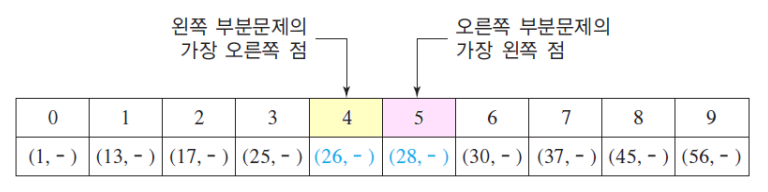
중간 영역에 속한 점 = {왼쪽 부분 문제의 가장 오른쪽 점(왼쪽 중간점)의 x-좌표에서 d를 뺀 값과 오른쪽 부분 문제의 가장 왼쪽 점 (오른쪽 중간점)의 x-좌표에 d를 더한 값 사이의 x-좌표 값을 가진 점들}
예로 d가 10이라면 (25,-),(26,-),(28,-),(30,-),(37,-)이 중간 영역

중간 영역에 있는 점들을 y좌표 기준으로 정렬 => O(nlogn)
정렬된 y좌표 기준으로 중간 영역 탐색 시작

Pseudo code

ClosestPair(S)
입력: x-좌표의 오름차순으로 정렬된 배열 S에는 i개의 점(단, 각 점은 (x,y)로 표현된다.)
출력: S에 있는 점들 중 최근접 점의 쌍의 거리
1. if(i<=3) return (2또는 3개의 점들 사이의 최근접 쌍)
2. 정렬된 S를 같은 크기의 Left_S 와 Right_S로 분할한다. 
    단, |s|가 홀수이면, |Left_S| = |Right_S|+1이 되도록 분할한다.
3. Left_ClosestPair = ClosestPair(Left_S)
4. Right_ClosestPair = ClosestPair(Right_S)
5. d=min{dist(Left_ClosestPair),dist(Right_ClosestPair)}일 때, 
    중간 영역에 속하는 점들 중에서 최근접 점의 쌍을 찾아서 
    이를 Center_ClosestPair라고 하자. dist()는 두 점 사이의 거리
return(min(dist(Left_ClosestPair),dist(Right_ClosestPair),dist(Center_ClosestPair))

수행 과정

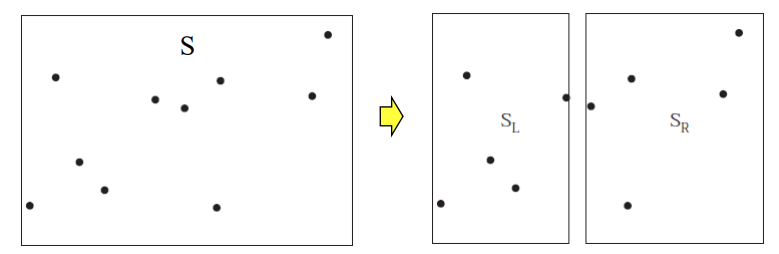
ClosestPair(S)로 호출
- 초기 점의 수가 >3 으로 분할 과정을 거친다.

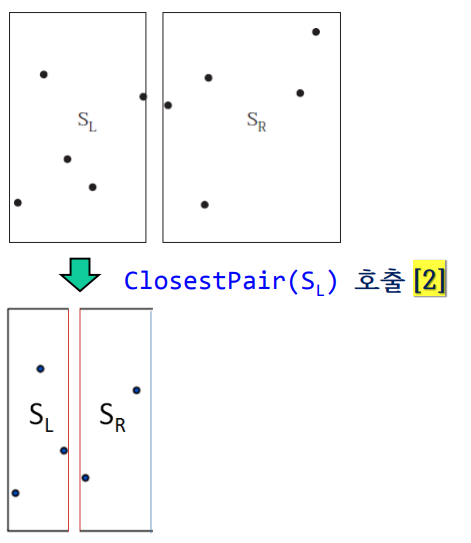
왼쪽의 경우: 아직 점이 3개보다 많으므로 3개가 될 때 까지 점을 다시 분할한다.

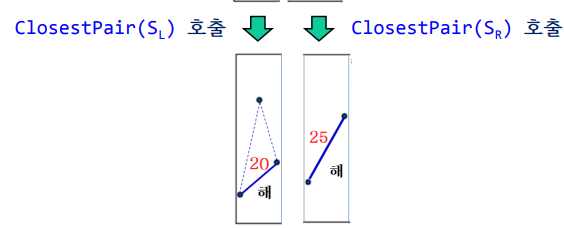
이렇게 점이 3개, 2개까지 분할이 되었으므로 각 점의 최소 거리를 찾는다.

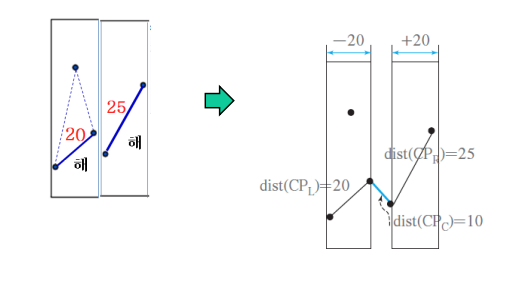
최소 부분 문제 까지 접근했으므로 이제 분할을 하나로 합치는 과정이 필요하다.
하나로 합치는 과정은 왼쪽 오른쪽 분할 중에서 가장 최소 거리를 골라서 그 범위 내의 중간영역 중 최소 거리 쌍을 찾는다.
원래의 리스트로 합쳐질 때 까지 중간 영역 중 최소 쌍을 찾아가면서 돌아온다.

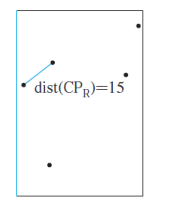
왼쪽을 분할 정복한 결과

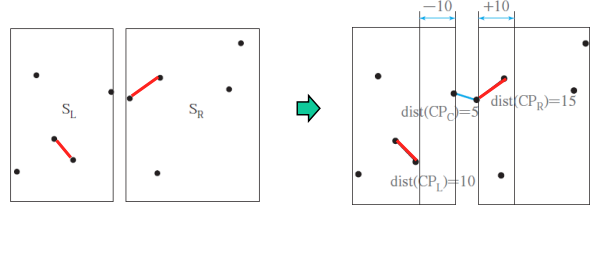
똑같이 왼쪽 오른쪽중 최소거리를 고른 다음 최소거리만큼 중간 영역 중에서 최소 거리 쌍을 찾는다.

시간 복잡도

S에 n개의 점이 있으면 전처리 과정으로 정렬: O(nlogn)
Line 1: S에 3개의 점이 있는 경우에 3번의 거리 계산이 필요하고, S의 점의 수가 2이면 1번의 거리 계산이 필요하므로 O(1) 시간 소요
Line 2: 정렬된 S를 왼쪽과 오른쪽으로 분할하는데, 이미 배열에 정렬되어 있으므로, 배열의 중간 인덱스로 분할하면 된다. O(1)
Line 3~4: 왼쪽 리스트와 오른쪽 리스트에 대하여 각각 최소거리 쌍을 호출하는데 분할하여 호출되는 과정은 합병정렬과 동일
Line 5:
- d = min(dist( $CP_L$ ), dist( $CP_R$ ))일 때 중간 영역에 속하는 점들 중에서 최근접 점의 쌍을 찾는다.
- 이를 위해 중간 영역에 있는 점들을 y좌표 기준으로 정렬한 후에 아래에서 위로 각 점을 기준으로 거리가 d 이내인 주변 점들 사이의 거리를 각각 계산하며, 이 영역에 속한 점들 중에서 최근접 점의 쌍을 찾는다.
- y좌표 정렬에 O(nlogn)이 걸리고, 거리 계산에는 O(1)이 소요된다.
Line 6: 3개의 점의 쌍 중에서 가장 짧은 거리를 가진 점의 쌍을 리턴하므로 O(1) 소요
ClosestPair 알고리즘의 분할과정은 합병정렬과 동일
- 그러나 알고리즘 내에서 해를 취합하는 과정인 Line5~6 과정에서 따로 O(nlogn) 필요
k층 까지 분할된 후, 층별로 line 5~6이 수행되는 과정을 보여준다.
- 각 층의 수행 시간은 O(nlogn)
- 여기서 각 층 수인 logn을 곱하면 O(nlog^2n)

Python 구현

import random, time, math


# p와 q가 각각 세개의 값으로 이루어짐 
def dist(p, q):
    return math.sqrt((p[0]-q[0])**2 + (p[1]-q[1])**2)


def closest_pair(a, low, high): # 점들의 배열 a, low,high => 고려해야할 범위
    size = high - low + 1
    if size == 2:
        return [low, high, dist(a[low], a[high])] #내부 점이 2개인 경우, low,high,거리를 반환한다
    if size == 3: 
    # 3개인 경우, 각 low,high를 구하고, 최소거리를 반환한다.
    #low, low+1 high ==> 각 점들을 보유한 배열의 인덱스임
        s = [[low,   low+1, dist(a[low], a[low+1])], 
             [low,   high,  dist(a[low], a[high])], 
             [low+1, high,  dist(a[low+1], a[high])]]
        [x, y, z] = min(s, key=lambda arr: arr[2])
        return [x, y, z]

    mid = size // 2 + low - 1

    left_pair = closest_pair(a, low, mid)
    right_pair = closest_pair(a, mid+1, high)

    d = min(left_pair[2], right_pair[2]) # strip의 한쪽 길이

    l_boundary = min(z for x, y, z in a if x >= a[mid][0] - d)
    r_boundary = max(z for x, y, z in a if x <= a[mid][0] + d)
    # strip은 y-좌표로 정렬되도록 b[]로부터 가져온다.
    # 원래 이때 y좌표 기준으로 정렬해야했음 
    strip = [[x, y, z] for x, y, z in b if z >= l_boundary and z <= r_boundary ]

    # 중간 영역에서 최근접 점의 쌍을 찾기
    c = [[strip[i][2], strip[j][2], dist(strip[i], strip[j])] 
          for i in range(len(strip)) for j in range(i+1, len(strip)) if i != j]

    center_pair = [-1, -1, float('inf')]
    if len(c) > 0:
        center_pair = min(c, key=lambda arr: arr[2]) 

    t = [left_pair, right_pair, center_pair]
    return min(t, key=lambda arr: arr[2])  # 최소 거리 쌍 찾기


#N = 20
#a = []
#random.seed(time.time())
#for i in range(N):
#    x = random.randint(0, 200)
#    y = random.randint(0, 100)
#    a.append([x, y])
a = [[3,3], [8,3], [4,6], [11,7], [6,6], [6,8], [5,1], [1,7], [11,1], [10,9]]
N = len(a)

a.sort(key=lambda t: t[0])  # x-좌표로 정렬
for i in range(N):
    a[i].append(i)
print(a)
b = a[:]
b.sort(key=lambda t: t[1])  # y-좌표로 정렬 # 트릭, y축으로 정렬된 배열을 준다. x축에 대한 rank는 그대로 남아있다.

result = closest_pair(a, 0, len(a)-1)
print('분할 정복 해 =\t', a[result[0]][:2], '\t', a[result[1]][:2], '\t %.2f' % result[2])

# O(N**2) 최적해 찾기
c = [[i, j, dist(a[i], a[j])] 
     for i in range(N) for j in range(i+1,N) if i != j]
c_pair = min(c, key=lambda arr: arr[2]) 

print('N**2 해    =\t', a[c_pair[0]][:2], '\t', a[c_pair[1]][:2],'\t %.2f' % c_pair[2])
print(c_pair[2] == result[2])