서론
자동차중 뭐가 더 빠른지 확인하기 위해 km란 단위를 사용합니다. 단거리 육상 선수가 얼마나 빠른지 몇초만에 50m를 주파하는지 검사합니다. 알고리즘에서는 뭐가 더 좋은 알고리즘일까요? 만약 어떤게 더 좋은 알고리즘이라면 어떤 기준으로 정할까요?
이번 게시물에는 어떤 기준으로 정하는지 어떻게 그 기준을 구하는지 배워 보겠습니다.
좋은 알고리즘이란
- 수행시간이 적음
- 사용된 메모리 공간이 적음
알고리즘의 평가 기준
- 공간 복잡도: 알고리즘 수행에 필요한 메모리 공간
- 시간 복잡도: 알고리즘의 수행시간 (일반적으로 시간복잡도로 많이 비교)
공간 복잡도란(Space Complexity)
- 공간 복잡도: 고정 공간 + 가변 공간
- 고정 공간: 문제의 instance에 무관한 일정한 양의 메모리 공간
- 가변 공간: 문제의 instance에 따라 가변적인 메모리 공간
예시 1
float sum(float list[], int n) {
float tempsum = 0;
int i = 0;
for (int i = 0; i < n; i++) {
tempsum += list[i];
}
return tempsum;
}위 알고리즘에서
- 고정 공간: i, n , tempsum
- 가변공간:list[]이다
이것이 가변 공간인 이유는 call by reference로 언어마다 다르겠지만
입력 instance마다 공간의 크기가 달라지기 때문이다
- 총 공간의 양: 2*sizeof(int) + sizeof(float) + ? 이다 ?는 가변공간
시간 복잡도란(Time Complexity)
- 프로그램 구현 없이 알고리즘에서 문장이 수행되는 스텝 수를 계산하여 분석
- 스텝 수의 계산 방법
- s/e(steps/execution): 각 문장에 대한 스텝 수 계산
- Frequency: 각 문장이 실행되는 빈도 계산
- 각문장에 대한 총 스탭수 == 시간 복잡도
SUM (s/e)X(frequency)
+변수의 선언은 step으로 계산 X-시간 복잡도 예
예시 2
void add(int a[][M_SIZE]) {
int i, j;
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++) {
c[i][j] = a[i][j] + b[i][j];
}
}
}
위 예시를 보고 시간복잡도를 구해보겠습니다.
선언은 step 수 포함이 안되기 때문에 매개인자 부분과 1번째줄은 step 수는 0이다.
그리고 for문의 조건식 부분은 m번 반복 된다고 생각할 수 있는데 마지막에 반복문을 빠져나올때 조건식 검사를 하기 때문에 m+1번반복하고 반복문 안에 실행문은 m번 반복한다.
그럼 아래 for문은 m(n+1)번 반복할 것이다.
마지막으로 안에 실행문은 mn번 반복한다.
따라서 시간 복잡도는 총합인 2mn + 2*m +1인 것을 볼 수 있다.
점근적 표기법을 쓰는 이유
위에 공간 복잡도와 시간 복잡도를 사용해서 비교하면 정확할 순 있지만 다른 알고리즘과 비교하기 어렵습니다.
그래서 저희는 점근적으로 표기하여 어떤 알고리즘이 기껏해야 어느 정도 보다 크고 적어도 어느 정도 보다 작다로 표기하여 알고리즘의 효율성을 비교하기 쉽게 표기합니다.
점근적 표기법
- 정확한 단계 수를 대신하여 수학적 기호를 사용하여 표현(점근적 표기법)
- 알고리즘의 입력 크기 변화에 따른 수행 시간 예측
- 동일 문제에 대한 다른 알고리즘 비교
- 표기방법
- Big-oh(O): 상한 표현 (일반적으로 상한 표현을 많이 사용)
- Omega(Ω) : 하한 표현
- Theta(θ): 상한-하한 표현
일반적으로 알고리즘을 비교할때 상한 표현인 빅오를 사용합니다.
Big-Oh 표기법
정의: 모든 n에 대해 f(n) ≤ Cg(n) (여기서 C ≥ 1)이 성립할 때, f(n)의 시간 복잡도를 O(g(n))로 표기한다.
예
- 3n + 2 는 3n + 2 ≤ 4n 이기 때문에 g(n)은 n입니다. 따라서 O(n)입니다.
함수 - f(n) = 2n^2 + 5n + 3
이 함수에 대해 f(n) ≤ 3n^2 + 6n^2 (n ≥ 1) 이 성립합니다. 따라서 g(n)을 n^2으로 정의할 수 있으며, 이 함수의 시간 복잡도는 O(n^2)입니다.
함수 - f(n) = 5log(n) + 10
이 함수에 대해 f(n) ≤ 10log(n) (n ≥ 1) 이 성립합니다. 따라서 g(n)을 log(n)으로 정의할 수 있으며, 이 함수의 시간 복잡도는 O(log(n))입니다.
함수 - f(n) = 3n^3 + 4n^2 + 2^n
이 함수에 대해 f(n) ≤ 5n^3 + 5n^3 (n ≥ 1) 이 성립합니다. 따라서 g(n)을 n^3으로 정의할 수 있으며, 이 함수의 시간 복잡도는 O(n^3)입니다.
이처럼 빅오 표현 예들을 볼 수 있는데 이정도 예제들을 풀어보고 다양한 예제들을 접해보면
굳이 시간 복잡도를 하나하나 구하지 않아도 빅오로 표현 할 수 있습니다.
하한 표기법
정의: 함수 f(n)이 양의 상수 C와 함수 g(n)이 존재하여, 모든 n에 대해 f(n) ≥ Cg(n) (여기서 C > 0)이 성립할 때, f(n)의 시간 복잡도를 Ω(g(n))으로 표기합니다.
알고리즘의 최선의 경우 시간 복잡도를 나타냅니다. 하한 표기법은 빅오 표기법과 유사하지만, 알고리즘의 실행 시간이 아래로 제한될 때 사용됩니다.
예
- 함수 f(n) = 4n^2 + 3n + 1
이 함수에 대해 f(n) ≥ 2n^2 (n ≥ 1) 이 성립합니다. 따라서 g(n)을 n^2으로 정의할 수 있으며, 이 함수의 하한은 Ω(n^2)입니다. - 함수 f(n) = 7log(n) + 5
이 함수에 대해 f(n) ≥ log(n) (n ≥ 1) 이 성립합니다. 따라서 g(n)을 log(n)으로 정의할 수 있으며, 이 함수의 하한은 Ω(log(n))입니다. - 함수 f(n) = 2^n + 3n
이 함수에 대해 f(n) ≥ 2^n (n ≥ 1) 이 성립합니다. 따라서 g(n)을 2^n으로 정의할 수 있으며, 이 함수의 하한은 Ω(2^n)입니다.
Theta 표기법
함수 f(n)이 양의 상수 C1, C2와 함수 g(n)이 존재하여, 모든 n에 대해 C1g(n) ≤ f(n) ≤ C2g(n) (여기서 C1 > 0, C2 > 0)이 성립할 때, f(n)의 시간 복잡도를 Θ(g(n))으로 표기합니다.
즉, Theta(Θ) 표기법은 함수 f(n)이 g(n)의 상한과 하한으로 동시에 제한된다는 의미입니다. 이는 알고리즘의 실행 시간이 상한과 하한에 의해 제한되어 있다는 것을 나타냅니다.
Theta(Θ) 표기법을 사용하면 알고리즘의 성능을 보다 정확하게 평가하고, 최적의 알고리즘 선택이나 문제의 실행 시간을 예측하는 데 도움을 줄 수 있습니다.
[참고]
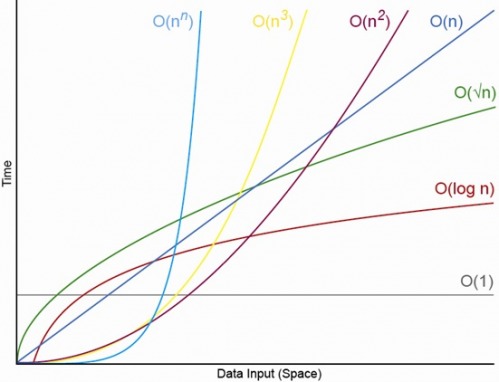
마지막으로 big-O 표기법의 수행시간 효율성 비교 이미지 입니다
𝑂(1) < 𝑂(log n) < 𝑂(n) < 𝑂(n log n) < 𝑂(n²) < 𝑂(n³) < 𝑂(2ⁿ) < 𝑂(n!)
순으로 효율적입니다.
