[논문리뷰] Deep Unsupervised Learning using Nonequilibrium Thermodynamics (DPM, 2015)
0
Diffusion Models
목록 보기
1/8
0. Abstract
- "Diffusion Model"을 최초로 제안한 논문
- non-equilibrium statistical physics에 착안함
1. Introduction
tractability & flexibility tradeoff
- tradeoff in probabilistic models
- models that are tractable
- e.g. Gaussian or Laplace
- can be analytically evaluated and easily fit to data
- 데이터셋이 너무 방대하면 모델링하는데 무리가 있음
- models that are flexible
- can be molded to fit structure in arbitrary data
- we can define models in terms of any (non-negative) function yielding the flexible distribution
- normalization constant 의 계산이 intractable하기 때문에 flexible model을 train/evaluate/inference 하려면 아주 많은 Monte Carlo process가 필요함
1.1. Diffusion probabilistic models (DPM)
- present DPM that allows
1. extreme flexibility in model structure
2. exact sampling
3. easy multiplication with other distributions (to compute posterior)
4. can cheaply evaluate log-likelihood and probability of individual states
2. Algorithm
2.0. Overview
- 먼저 target (data) distribution --> simple known (Gaussian) distribution으로 보내는 forward diffusion process를 정의
- finite-time reversal of diffusion process를 학습
- also derive entropy bounds
2.1. Forward Trajectory
- data dist. --> tractable dist. by repeated Markov diffusion kernel for where is the diffusion rate
- 은 Gaussian -> Gaussian(with identity coveariance) 또는 Binomial -> Binomial(independent)으로 보내는 kernel이다
2.2. Reverse Trajectory
- Gaussian/Binomial이고 continuous한 diffusion에 대해 (+ 충분히 작은 step size ), reverse process는 forward process와 같은 functional form을 가진다 (Feller, 1949)
- 학습할 때는
- Gaussian : 각 kernel의 mean 과 covariance
- Binomial : 각 kernel의 bit flip probability
- 를 학습한다
2.3. Model Probability
- 데이터에 대한 generative model의 확률은
- 원래 이 계산은 intractable하지만, 아래와 같이 바꿔 쓸 수 있다
- based on annealed importance sampling & Jarzynski equality
- instead evaluate the relative probability of forward & reverse trajectories, averaged over forward trajectories - This can be evaluated rapidly by averaging over samples from the forward trajectory
- For infinitesimal ,
- forward & diffusion kernel이 identical해짐
- then only a single sample from is required to evaluate the above integral
2.4. Training
- Training amounts to maximize the model log likelihood
- which has a lower bound provided by Jensen's inequality,
- Appendix B에 의해 는 anlytical하게 계산 가능한 entropies와 KL divergences로 정리된다
- 가 충분히 작아서 forward process reverse process가 되면
- training은 를 maximize하는 reverse Markov transitions 를 찾는 방향으로 진행됨
- - probability distribution estimation은 sequence of Gaussians로 이루어진 function을 regression한는 task로 reduced된다
2.4.1. Setting the Diffusion Rate
- beta scheduling은 모델 성능에 큰 영향을 미침
- Gaussian의 경우 를 의 gradient ascent에 따라 달라지게 설정했음
- 단, overfitting을 막기 위해 은 small constant로 고정 - Binomial의 경우 로 freeze
- 후속 연구들에 따르면 Gaussian도 fixed schedule로 고정하는 게 낫다고 함
2.5. Multiplying Distributions, and Computing Posteriors
2.5.1. Modified Marginal Distributions
2.5.2. Modified Diffusion Steps
2.5.3. Applying
2.5.4. Choosing
2.6. Entropy of Reverse Process
3. Experiments
3.1. Toy Problems
-
3.1.1. Swiss Roll
-
2D swiss roll dist. 학습
-
RBF network로 mean 과 covariance 생성하게 함
-
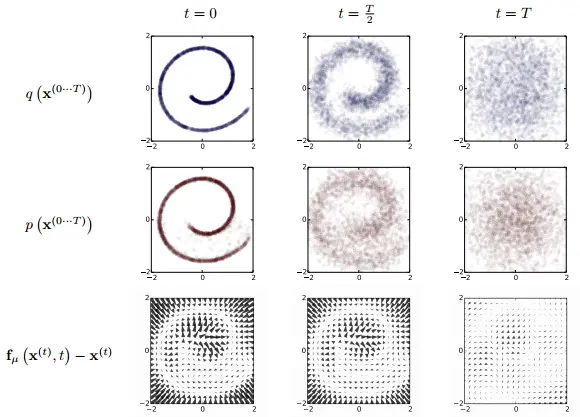
-
그림에서 세 번째 행은 drift term에 해당함
-
-
3.1.2. Binary Heartbeat Distribution
- length 20짜리 simple binary sequences로 학습
- 1 occurs every 5th time bin (나머지는 0)
- MLP로 Bernoulli rates 생성하게 함
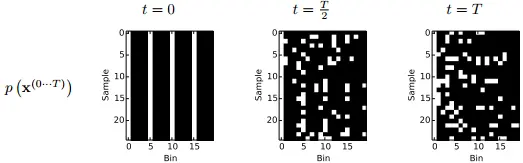
- length 20짜리 simple binary sequences로 학습
3.2. Images
- multi-scale convolutional architectures used
- MNIST, CIFAR-10, Dead Leaf Images, Bark Texture Images
- generation & inpainting task
Appendix
A. Conditional Entropy Bounds Derivation
B. Log Likelihood Lower Bound
-
initial lower bound of the log likelihood
-
B.1. Entropy of

-
B.2. Remove the edge effect at

- B.3. Rewrite in terms of posterior

- B.4. Rewrite in terms of KL divergences and entropies

