- 수백만개의 숫자중에서 원하는 숫자를 매일 하나씩 찾을 것이다.
매일 수백만개의 숫자중에서 단 하나의 숫자만 바뀐다.
어떤 알고리즘을 사용할 것인가?
1. 버블 정렬 (Bubble Sort)
버블 정렬은 배열에서 2개씩 선택하여 크기를 비교하고 스왑하는 것을 반복한다.
더 좋은 알고리즘들이 많기에 자주 쓰이진 않지만 이해하기가 굉장히 쉬운편임

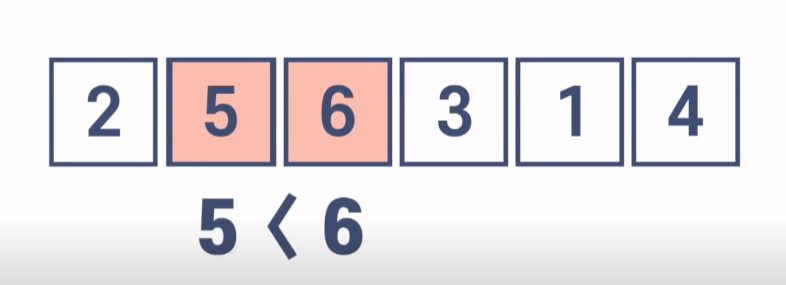
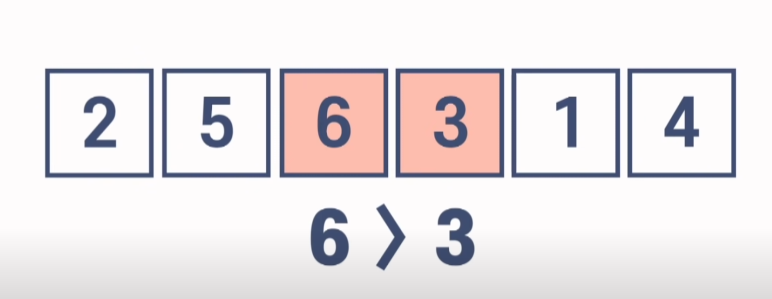
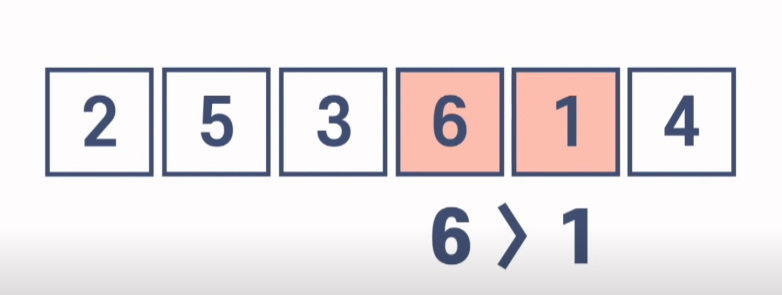
- Time Complexity of Bubble Sort
(n-1) + (n-2) + .... 2 + 1 -> n(n-1)/2 이므로 O(n^2) 의 시간 복잡도를 가진다 .
중간에 정렬이 완료되었음에도 마지막 회차까지 2개의 원소를 계속 비교하기 때문에 최선, 평균, 최악의 경우 모두 O(n^2) 의 시간 복잡도를 가진다.
2. 선택 정렬 (Selection Sort)

1) 전체 아이템 중에서 가장 작은 아이템의 위치를 찾는다

2) 가장 첫번째 아이템과 스왑한다.

3) 1은 이제 정렬된 부분이므로 나머지 정렬되지 않은 부분에서 다시 가장 작은 값을 찾는다.

4) 2는 가장 작으면서 가장 앞에 있으므로 스왑하지 않는다.
- Time Complexity of Selection Sort
먼저 버블 정렬과 비슷하게 비교와 스왑하는 부분이 있다. 정렬되지 않은 배열에서 가장 작은 숫자를 찾는 것은 N-1 의 비교를 하는 것이다. 하지만 버블정렬과 다르게 항상 N번의 스왑을 하지 않기에 2배정도 빠르다고 알려져 있지만 최댓값을 배열 전체에서 찾고 O(n) , 그것을 N번 반복하기에 O(n^2) 의 시간 복잡도를 가진다 .
3. 삽입 정렬 (Insertion Sort)
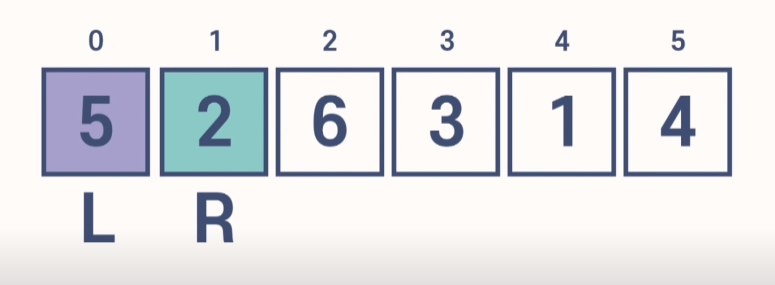
1) 두번째 아이템을 선택 후 왼쪽에 자신보다 큰 값이 있다면 그 값의 앞으로 이동한다.
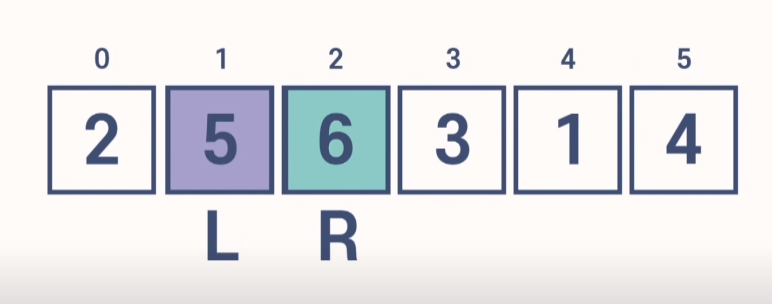
2) 세번째 아이템을 선택 했지만 왼쪽에 자신보다 큰 값이 없으므로 패스
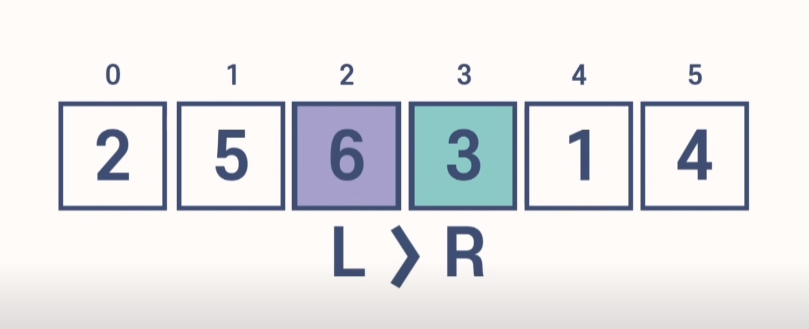
3) 3을 선택하고 왼쪽에 6을 보면 자신보다 크므로 스왑, 그다음 5도 자신보다 크므로 스왑 2는 자신보다 작으므로 멈춘다.
- Time Complexity of Insertion Sort
삽입 정렬은 필요한 아이템만 스캔하기 때문에 선택 정렬, 버블 정렬보다 빠르다.
그러나, 결국 시간복잡도는 O(n^2)으로 동일하다. 결국 최악의 경우엔 가장 작은 값이 맨 뒤쪽에 있으면 맨 앞까지 비교하면서 스왑이 이뤄지기 때문.
하지만 선택 정렬의 경우 이미 정렬이 되어있는데 하나의 값만 삽입해서 다시 정렬하는 경우 O(n) 의 시간복잡도를 가진다는 특징이 있다. 이미 정렬된 경우에는 삽입 정렬이 굉장히 효율적이다.

4. 머지 정렬 (Merge Sort)

1) 먼저 배열을 반씩 계속 나눠서 2개의 값을 가질 때까지 나눈다. (재귀 함수 호출)
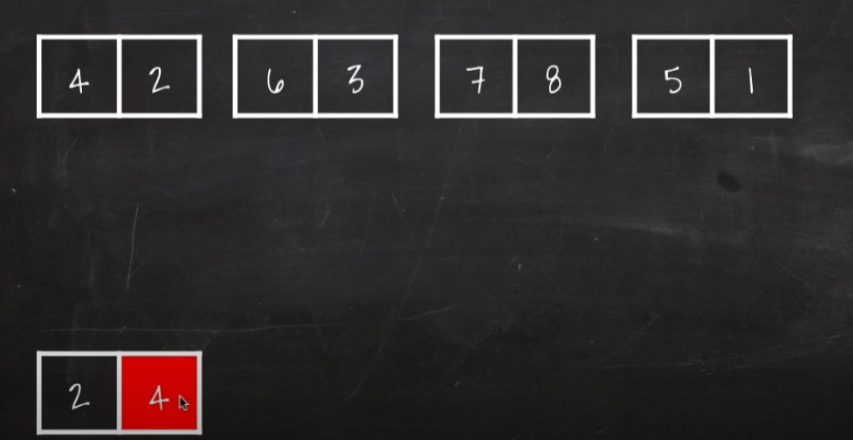
2) 복사된 2칸 배열에 작은 값을 앞으로 보내서 정렬한다.

3) 정렬된 배열을 다시 원래 배열로 복사한다.

4) 이렇게 모든 파티션을 각각 정렬한다.

5) 그럼 이제 앞의 두개의 파티션을 병합한다. 가장 작은 값부터 비교하면서 새로운 배열에 작은값부터 채워 넣는다.





- Time Complexity of Merge Sort

파티션이 낱개가 될때까지 자르므로 N번 재귀함수가 호출되고, 자를 때마다 검색해야하는 데이터 양이 절반씩 줄어드므로 log n 만큼 검색하여 O(nlogn) 의 시간복잡도를 가진다. 다만 단점으로는 계속 배열을 복사하는 과정에서 메모리를 많이 쓰므로 공간복잡도가 크다.
5. 퀵 정렬 (Quick Sort)
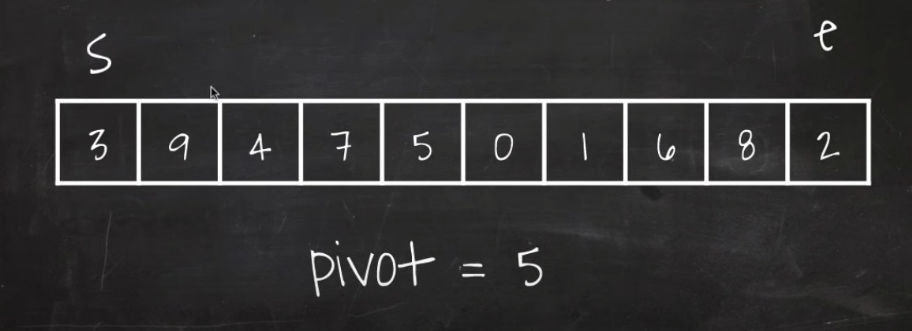
1) 피봇을 골라서 피봇보다 작은건 왼쪽, 큰건 오른쪽으로 옮긴다. 배열의 양 끝에 start , end 포인터를 둔다
start 포인터는 피봇보다 작은 값은 무시하면서 증가하고
end 포인터는 피봇보다 큰 값은 무시하면서 감소한다.
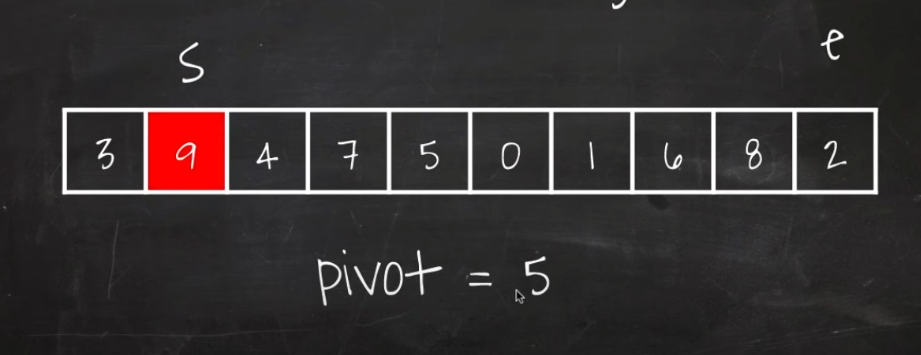
2) start 포인터가 가르킨 9가 피봇보다 크므로 멈춘다.
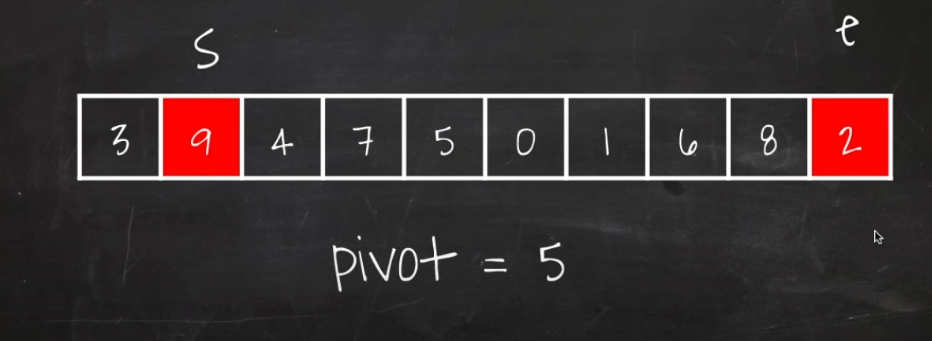
3) end 포인터가 가르키는 2가 피봇보다 작으므로 멈춘다.
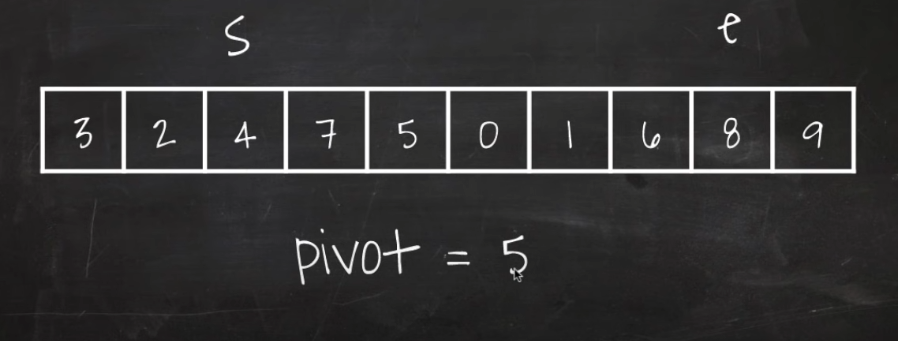
4) 두 값을 스왑후 start 와 end 를 다음 값으로 옮기고 반복.

5) start 는 4를 건너뛰고 7에서 스탑, end 는 8 6 을 건너뛰고 1에서 스탑
그리고 스왑한다.
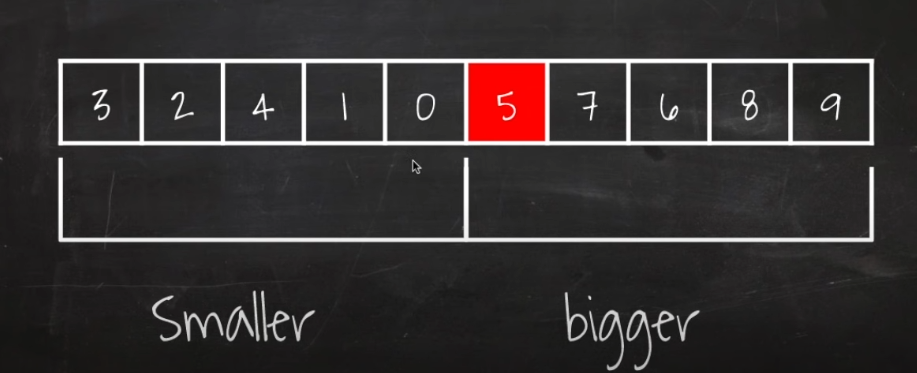
6) 사이클이 진행되면 피봇보다 작은값들 , 큰값들로 파티션이 나뉨
파티션들에서 다시 피봇을 고르고 퀵소트를 재귀적으로 진행한다.
- Time Complexity of Quick Sort

1) 피봇을 골라서 피봇보다 작은건 왼쪽, 큰건 오른쪽으로 옮긴다.
즉 피봇이 중간값을 가지면 좋지만 검색해보고 뽑는게 아니므로 배열의 가운데 있는 값을 그냥 고른다.

2) 피봇이 최소값이었기때문에 0을 맨 앞으로 보내고 나머진 다 오른쪽에 둔다.
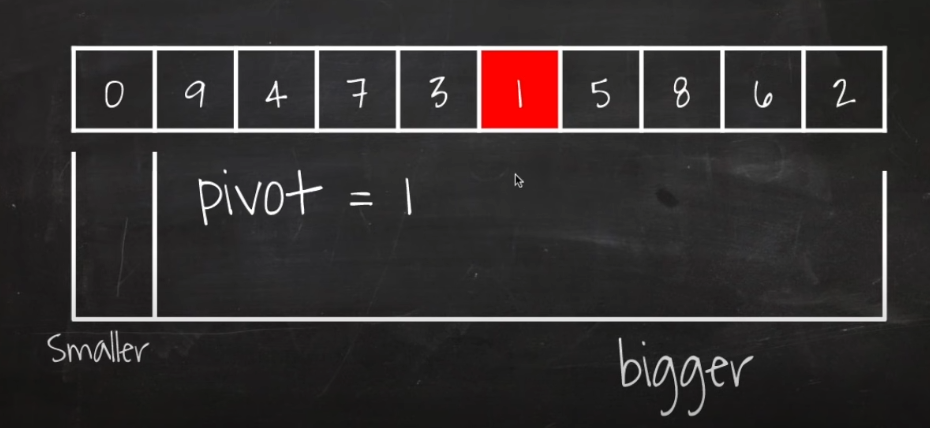
3) 왼쪽은 값이 하나라 정렬이 끝났고 오른쪽 파티션에서 다시 피봇을 고른다.
또 피봇이 최소값이었기 때문에 1을 맨 왼쪽으로 고르고 다시 파티션에서 피봇을 고른다.
즉 피봇이 계속 최소값 or 최대값인 경우엔 최악의 경우이며 이때 O(n^2) 의 시간복잡도를 가지게 된다. 그러나 일반적으로는 O(nlogn)의 시간복잡도를 가진다.
참고로 자바에서 우리가 자주쓰는 Arrays.sort() 의 내부 알고리즘은 피봇을 2개 쓰는 Dual Pivot Quick Sort 이다. 이론적, 실험적으로 랜덤 데이터에 대해 보통 퀵소트보다 상당히 좋은것으로 판명되었으나 역시나 최악의 경우엔 O(n^2)임이 변하진 않는다.
Collections.sort()의 경우는 삽입정렬 + 머지 정렬인 Tim 정렬을 사용한다고 한다. 배열은 메모리적으로 각 값들이 연속적 주소를 갖기 때문에 참조 지역성이 좋은 퀵 정렬을 쓰고 Collections.sort()는 보통 어레이리스트뿐 아니라 메모리적으로 산발적인 링크드리스트도 사용하기에 참조 인접성이 좋지 않아서 Tim 정렬을 쓰는것이 평균적으로 더 좋다고 합니다.
맨 위에서의 질문의 답은 처음에 값이 수백만개가 있는 값 중에서 원하는 값을 찾기 위해선 처음에 머지소트나 퀵소트를 활용하여 정렬을 하고 이분 탐색을 하는것이 가장 효율적일 것이다.
매일 값이 하나 바뀌는 경우에 다시 값을 찾으려면 이분 탐색을 하기위해 매일 정렬을 새로해야하는데 이미 정렬이 되어 있으므로 삽입 정렬을 해주는 것이 가장 좋을 것이다.
[참고한 곳]
유튜브 엔지니어 대한민국 : https://www.youtube.com/user/damazzang
유튜브 노마드 코더 : https://www.youtube.com/channel/UCUpJs89fSBXNolQGOYKn0YQ
http://www.secmem.org/blog/2019/05/06/special-sorts-2/
https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html
https://velog.io/@gillog/%EB%B2%84%EB%B8%94-%EC%A0%95%EB%A0%ACBubble-Sort
https://devuna.tistory.com/28
https://github.com/GimunLee/tech-refrigerator