[TIL#31 350403] M몰라요 Z잘래요

강민지·2025년 4월 3일

데이터분석_TIL

목록 보기

33/81

Daily plan

🌞오전

- 통계 라이브세션 정리
- 10시 통계 라이브세션 듣고 정리

🔥 오후

- 14시 파이썬 스탠다드 이론 수업 + 이론 복습
- 정리해놓은 빅분기 이론 복습

🌝 저녁

- 통계 강의는 언제 듣냐.....
- QCC 준비는 언제 하니......
- 19시 파이썬 스탠다드 실습 수업
- 스크럼 작성 + TIL 제출

통계 라이브세션 1회차

데이터 종류

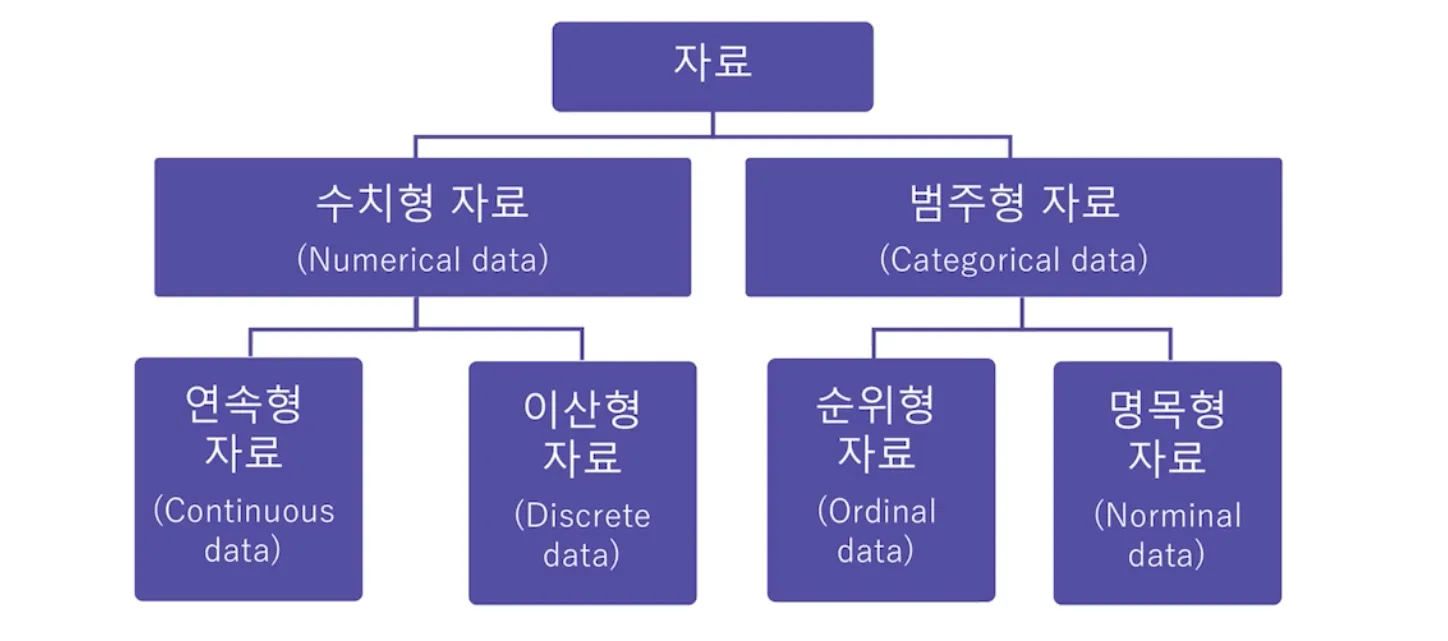
편차, 분산, 표준편차

편차(deviation): 하나의 값에서 평균을 뺀 값 (= 평균으로부터 얼마나 떨어져 있는지)
분산(variance): 편차의 합이 0으로 나오는 것을 방지하기 위해 생성된 개념 (= 편차 제곱합의 평균)
표준편차(standard deviation(σ)): 분산에 제곱근을 씌워준 값 (원래 단위로 되돌리기 위해 제곱근을 씌움)

표본분포

표본분포: 표본통계량으로부터 얻은 도수분포 (표본의 분포)
- 표본평균의 분포
  : 모집단에서 여러 표본 추출 후 각 표본의 평균 계산시, 중심극한정리에 따라 정규분포에 가까워짐. 즉, 표본 크기가 충분히 크다면 표본 평균이 정규분포를 따름.
- 표본분산의 분포
  : 모집단에서 여러 표본 추출 후 각 표본의 분산을 계산하면, 표본분산들의 분포는 카이제곱 분포을 따름. 이는 모집단이 정규분포를 따를 때보다 높게 성립됨.
표준오차: 표본의 표준편차 (표본평균의 평균과 모평균 간의 차이)

도수분포표

도수: 특정 구간에 발생한 값의 수
상대도수: 특정 도수를 전체 도수로 나눈 비율
도수분포표: 각 값에 대한 도수와 상대도수를 나타내는 표
- 도수분포표 만들기
  1. 최댓값, 최솟값 계산
  2. 최댓값, 최솟값을 포함하여 데이터를 특정 범위(계급)로 나눔
  3. 각 계급을 대표하는 수치(=계급값) 정하기
  4. 각 계급에 포함된 데이터 개수(도수) 카운트
  5. 각 계급의 도수가 전체에서 차지하는 비율(상대도수) 계산
  6. 특정 계급까지의 도수를 모두 더함(누적도수)
히스토그램: 도수분포표를 활용하여 만든 막대그래프
임의표본추출: 무작위로 표본을 추출하는 것
편향: 한쪽으로 치우쳐져 있음

정규분포

정규분포
- 분포는 평균을 중심으로 좌우 대칭의 형태
- 곡선은 각 확률값을 나타내며, 모두 더하면 1이 됨
- 정규분포는 평균과 분산에 따라 다른 형태를 가짐
- 평균 0, 분산 1을 가지는 경우 이를 표준정규분포라고 함
표준정규분포
- 표준화(standard scaler): 분포의 평균과 분산값을 통일하여 확률 계산을 용이하게 하는 작업
- 확률변수X(값)에서 평균m을 빼고 표준편차로 나눈 값
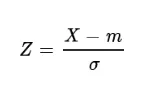
- 머신러닝 모델을 만들 때 데이터 범위가 많이 차이나는 경우 표준화가 필요함

신뢰구간, 신뢰수준

신뢰구간: 특정 범위 내에 값이 존재할 것으로 예측되는 영역
신뢰수준: 신뢰구간이 실제모수를 포함하게 되는 확률로, 주로 95%와 99%를 이용
- 신뢰수준 95%: 표본을 통해 얻은 결과가 실제 모집단의 특성을 95% 반영한다는 의미
python scipy라이브러리 코드 실습

import scipy.stats as st
import numpy as np

# 샘플 데이터
sample1 = [5, 10, 17, 29, 14, 25, 16, 13, 9, 17]
sample2 = [21, 22, 27, 19, 23, 24, 20, 26, 25, 23]

df= len(sample1)-1  # 자유도 = n-1
mu = np.mean(sample1) # 표본 평균
se = st.sem(sample1) #표준 오차

# 95% 신뢰구간
st.t.interval(0.95, df, mu, se)

# 99% 신뢰구간
st.t.interval(0.99, df, mu, se)

신뢰구간을 구할 때 일반적으로 표준오차를 사용함
표준편차로 각 값이 평균으로부터 얼마나 떨어져 있는지 파악한 후,
표준오차를 통해 표본의 평균이 얼마나 정확하게 모집단의 평균을 추정하는지 나타냄

통계 라이브세션 2회차

통계적 실험

특정 가설을 확인하거나 기각하기 위한 목표로 실험 설계
통계와 직감의 밸런스를 잘 맞추기!
변수: 대상의 속성이나 특성을 측정하여 기록한 것
독립변수(설명변수): 원인이 되는 변수
종속변수(결과변수): 결과가 되는 변수, 독립변수에 따라 그 값이 변할 것이라고 예상하는 변수
모수: 모집단을 대표하는 값
모수통계: 모집단이 정규분포를 따른다는 가정 하에 사용. 평균, 분산 등의 값을 알고 있다는 가정 하에 진행하는 통계분석
비모수통계: 모집단이 정규분포가 아닌 경우, 즉 표본의 크기가 충분히 크지 않은 소규모 실험에서 사용. 평균, 분산 등의 값을 가정하지 않고 진행하는 통계분석
통계적 실험
- 어떤 목적을 가지고 관찰을 통해 결과(측정값)를 얻어내는 것
- 통계적 추론을 통해 보다 사실에 가까운 값을 도출하려는 목적
- 프로세스: 가설 수립 > 실험 설계 > 데이터 수집 > 추론 및 결론 도출

A/B TEST

두 가지 처리 방법 중 어느 하나가 더 좋다는 것을 입증하기 위해 실험군을 두 그룹으로 나누어 진행하는 실험 (버킷테스트, 분할테스트라고도 함)
목적
- UI/UX 개선
- 전환율 증가
- 매출 증가
주요 지표
- 서비스 가입률
- 재방문율
- CTR(노출 대비 클릭률), CVR(클릭 대비 전환율, 구매전환율)
- ROAS(캠페인 비용 대비 캠페인 수익)
- eCPM(1000회 광고 노출당 얻은 수익)
test그룹과 control그룹으로 나누어 진행하지만, 꼭 2개의 그룹으로 나눌 필요는 없음
- 일반적으로 두가지 방법 중 하나는 기준이 되는 기존 방법이거나 아예 아무 처리도 적용하지 않은 방법
프로세스
1. 현행 데이터 탐색
2. 가설 설정
  - 비즈니스 목표 달성에 필요한 KPI 정의
  - KPI 전환율 증가를 위한 귀무가설, 대립가설 설정
  - 귀무가설: 통계학에서 처음부터 버릴 것을 예상하는 가설, 차이가 없을 것을 가정
  - 대립가설: 귀무가설에 대립하여 차이가 있을 것을 가정
3. 유의수준 설정
  - 귀무가설이 맞을 때 오류를 얼마나 허용할 것인지 기준을 정하는 단계
4. 테스트 설계 및 실행
  - 사용자를 대조군, 실험군의 두 그룹으로 분리
5. 테스트 결과 분석
  - 측정 항목(가설)에 대해 두 그룹의 결과를 분석 (검정통계량 분석)
  - 대조군과 실험군 간 통계적으로 유의미한 차이가 있는지 확인
주의사항
- 적절한 표본크기
- 하나의 변수만 변경: 여러 변수를 동시에 변경하면 어떤 변수가 영향을 미쳤는지 파악할 수 없음
- 무작위성
- 적절한 분석 방법 선택, 유의수준 설정
- 통계적 유의미성뿐만 아니라 실제로도 의미있는 결과인지 한번 더 판단
- 동일하게 정해진 기간 동안 진행되어야 함 (기간이 짧으면 결과 수집이 어렵고, 너무 길면 사용자들의 행동이 변할 수 있음)

아티클 스터디

양질의 데이터를 판별하는 5가지 방법(5) - 목적에 적합한 데이터인가?

요약 : 양질의 데이터를 판별하는 가장 근본적인 방법은 분석과 활용 목적에 적합한 데이터를 선택하는 것! DIKW 피라미드 이론
- Data 데이터 → Information 정보 → Knowledge 지식 → Wisdom 지혜
- 데이터에서 지혜를 얻기 위해서 정보와 지식의 단계를 거쳐야 함
- 지혜, 지식, 정보를 담고 있는 데이터는 전체 데이터 중 일부임
  
  분석하고자 하는 내용이 담겨 있는 지를 기준으로 양질의 데이터를 판별하는 경우
  
  → 분석가의 역량에 따라 같은 데이터라도 양질의 데이터인지 여부가 달라질 수 있음
  
  → 숨은 정보를 끌어낼 수 있는 분석가의 역량도 필요!
  
  분석 방법에 부합한 데이터인지 여부도 고려해야 함
- 머신러닝을 위한 빅데이터
  - 충분한 데이터의 양
  - 종속 변수가 존재해야 함
- 인사이트 도출을 위한 빅데이터
  - 활용 가치 높은 정보가 데이터에 숨어 있는지 고민
  - 인사이트 활용 및 설명을 위 지수(index)개념이 활용되는 경우가 많음
  - 즉, 인사이트 도출을 위해서 원천 데이터에서 어느 정도 가공되어야 함
  
  명확한 분석 목적을 가져야 함
주요 포인트 :
- DIKW 피라미드 이론
- 분석하고자 하는 내용이 담겨 있는가?
- 분석 방법에 부합한 데이터인가?
- 명확한 분석 목적을 설정했는가?
인사이트 : 데이터에서 의미를 찾아내는 과정이 재밌기도 하지만, 분석가의 역량이 받쳐주지 않는다면 아무리 좋은 데이터에서도 유의미한 인사이트를 찾아내지 못 하거나 완전히 잘못된 방향으로 해석할 수도 있다는 게 무섭기도 하다. 많은 경험과 넓은 시야, 비판적이면서도 수용적인 태도가 필요할 것 같다.

[공통 인사이트]
데이터의 양질을 파악하는 것의 기준은 모호하며, 여러 기준에 따라 데이터의 양과 질을 결정하게 된다. 그 중에서도 중요한 것은 분석가의 역량으로 판가름이 난다. 가장 중요한 것은 분석의 목적을 명확하게 잡지 못 한다면 데이터의 품질을 논할 수 없다는 것이다.

Python Standard 1회차

- Long Format과 Wide Format 변환을 이해한다.
- melt, stack, unstack을 활용한 데이터 고급핸들링 기법을 숙지한다.
- 실습을 통해 이를 응용한다.

개념 이해

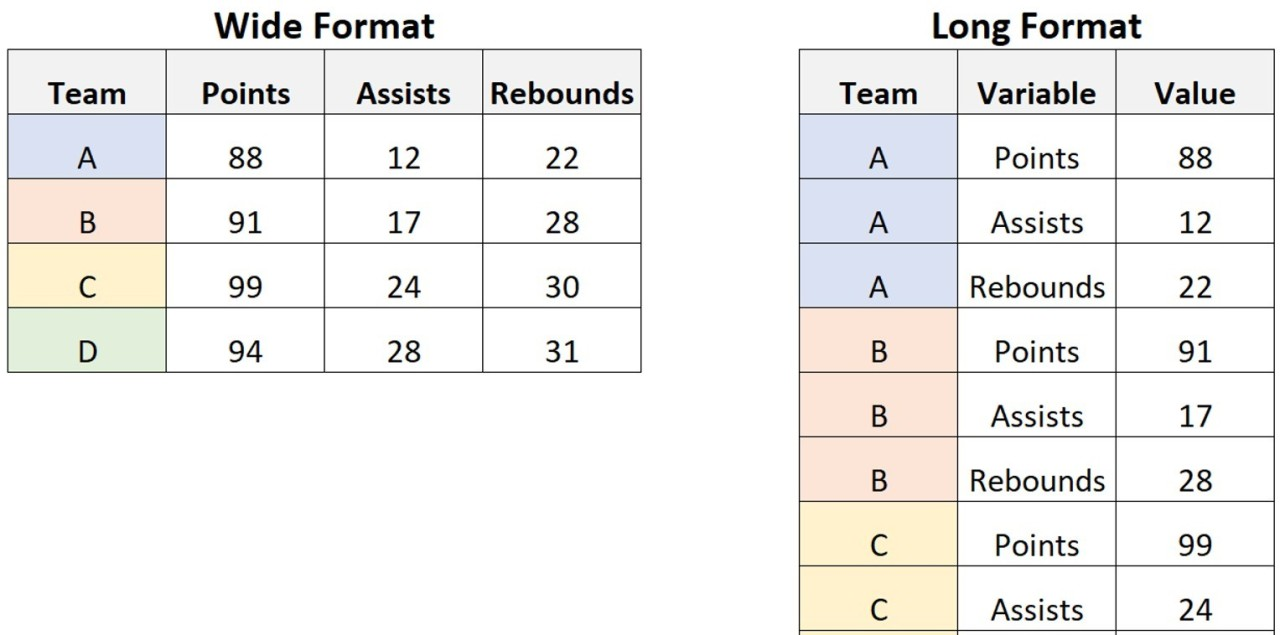
Wide Format
- 각 주제 또는 관찰 단위가 단일 행으로 표시되는 구조
- 한 대상에서 측정한 여러 측정값을 모두 한 행에 표시하고
- 열 이름으로 그 측정값의 의미를 나타냄
Long Format
- 하나의 열에 데이터를 나타내고 다른 열에 데이터에 대응하는 변수를 나타낸 형태
- 데이터를 기록할 때 하나의 관찰값이 하나의 행에 위치하도록 하는 형태

함수

Transpose

데이터의 열과 행을 바꿔주는 전치 함수
문법: df.T
열이 많을 경우 간단한 행렬전환을 통해 구조를 살펴볼 수 있음
데이터 크기가 크면 시간이 오래 걸릴 수 있으므로 행렬전환 이전에 구조를 파악해야 함

Pivot Table

Index, Columns, Values, Aggfunc을 직접 선언하여 테이블을 변환하는 함수로, 특정 열을 기준으로 데이터를 요약하고 새로운 형태의 표로 변환함
문법: pd.pivot_table(df, index=컬럼명, columns=컬럼명, values=컬럼명, aggfunc=연산방식)
- index: 인덱스로 사용될 열
- columns: 열로 사용될 열
- values: 값으로 사용될 열
- aggfunc: 연산 방식
index, values, aggfunc 입력을 list 형식으로 지정할 수 있음
- index와 columns를 list 형식으로 입력하면 멀티 인덱스 기반 피벗테이블이 생성
- values를 list 형식으로 입력하면 각 연산을 포함한 피벗테이블 생성
- 연산 방식: sum, mean, std, count, nunique, max, min
columns는 생략 가능함

Melt

데이터프레임의 컬럼을 열로 바꿔주는 메서드
문법: df.melt(id_vars=None, value_vars=None, var_name=None, value_name='value', col_level=None, ignore_index=True)
- id_vars: 기준이 될 열
- value_vars: 기준열에 대한 하위 카테고리를 나열할 열을 선택
- var_name: 카테고리들이 나열된 열의 이름 설정
- value_name: 카테고리들의 값이 나열될 열의 이름 설정
- col_level: multi index의 경우 melt를 수행할 레벨을 설정
- ignore_index: 인덱스를 1,2,3,...,n으로 설정할 지 여부 (디폴트값은 True)
피벗 테이블을 기존 형태로 바꿔주는 역할

Stack

컬럼을 인덱스의 하위 레벨로 변환
문법: df.stack(level=-1, dropna=True)
- level: stack을 수행할 인덱스 레벨 지정 (기본값은 -1로, 마지막 인덱스 레벨을 사용)
- dropna: 스택을 수행한 결과에서 결측값 제거 여부 지정 (기본값은 True)
멀티인덱스 처리가 가능함

Unstack

인덱스 레벨을 컬럼으로 변환
문법: df.unstack(level=-1, fill_value=None)
- level: unstack을 수행할 인덱스 레벨 지정 (기본값은 -1로, 마지막 인덱스 레벨을 사용)
- fill_value: unstack을 수행한 결과에서 결측값을 채울 값 지정 (기본값은 None으로, 결측값을 그대로 둠)
멀티인덱스 처리가 가능함

일기

아침부터 통계 라이브세션에, 아티클 스터디, 파이썬 스탠다드 반 수업까지 하니까 빅분기 공부를 할 틈새가 없었다. 사실 틈새는 있었는데 내 체력이 바닥나버림... 통계 공부하느라 파이썬을 잊고, 파이썬 공부하느라 SQL을 잊어버림ㅋ 낼 QCC 걱정이다^^..
이제 슬슬 주말이 필요해지고 있는 거 같다. 공부 시간도 그렇고 내 체력도 그렇고 ㅎㅎㅎ
5월부터는 주말 시간도 생기니까 좀만 더 힘을 내보자! 화이팅,,

강민지

이전 포스트

[TIL#30 250402] 암기빵 구해요 (진짜 급함)

다음 포스트

[TIL#32 250404]

1개의 댓글

김서현

2025년 4월 4일

점점 얼굴의 생기가 없어지더라니... ㅍㅇㅌ

답글 달기