
✏ DFS/BFS는 그래프 탐색(=많은 양의 데이터 중 원하는 데이터를 찾는 과정) 알고리즘.
추가로 기억 ; 유클리드 호제법. A,B에 대해서 A를 B로 나눈 나머지가 R이면 A와 B의 최대 공약수는 B와 R의 최대 공약수와 같다.
추가로 기억 ; 모든 재귀함수는 반복문을 이용하여 동일한 기능을 구현할 수 있다. 재귀함수가 반복문보다 유리한 경우도 있고 불리한 경우도 있다. 컴퓨터가 함수를 연속적으로 호출하면 컴퓨터 메모리 내부 스택 프레임에 쌓인다. 그래서 스택을 사용해야할 때 스택 라이브러리 대신에 재귀함수를 이용하는 경우가 많다.
정의
1. DFS
= 깊이 우선 탐색. 깊은 부분을 우선적으로 탐색하는 알고리즘이다.
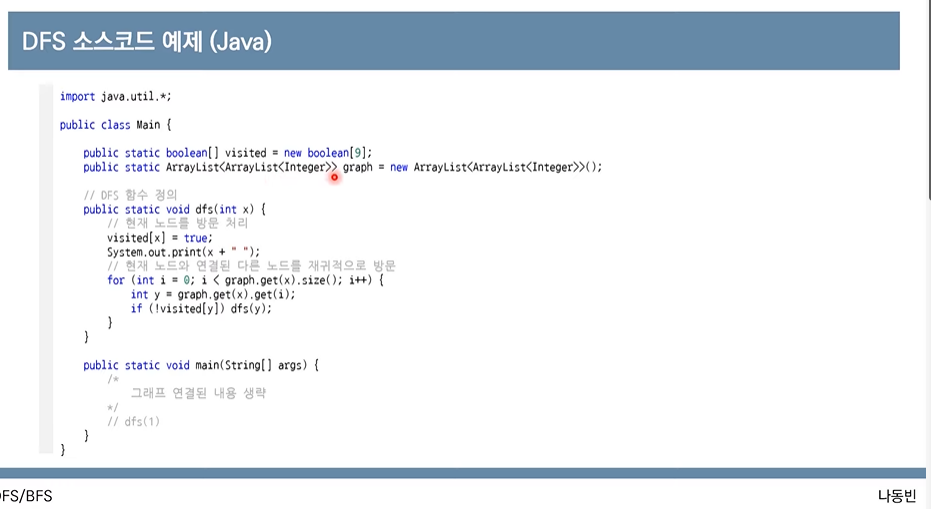
스택 자료구조(혹은 재귀함수를 이용한다.)
a. 탐색 시작 노드를 스택에 삽입하고 방문 처리를 한다.
b. 스택의 최상단 노드에 방문하지 않은 인접한 노드가 하나라도 있으면 그 노드를 스택에 넣고 방문 처리한다. 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼낸다.
c. b과정을 더이상 수행할 수 없을 때까지 반복한다.
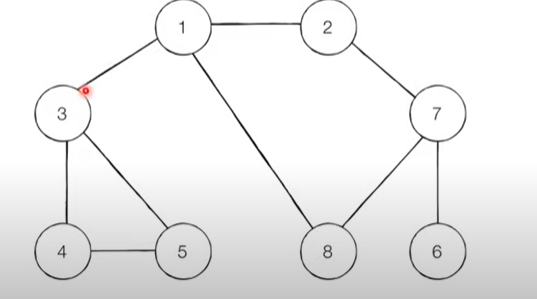
무방향 그래프. 인접한 노드가 여러개일때 어디부터 방문할지는 문제에 따라서 결정한다. 여기서는 번호가 낮은 인접노드부터 방문한다고 가정.
시작 노드 1을 스택에 삽입하고 방문처리하고 -> 인접한 노드 중 방문하지 않은거 스택에 삽입하고 방문 처리하고 .. 더이상 내려갈 수 없을 때 다시 돌아와서 깊은 방향으로 방문하게 된다.
2. BFS
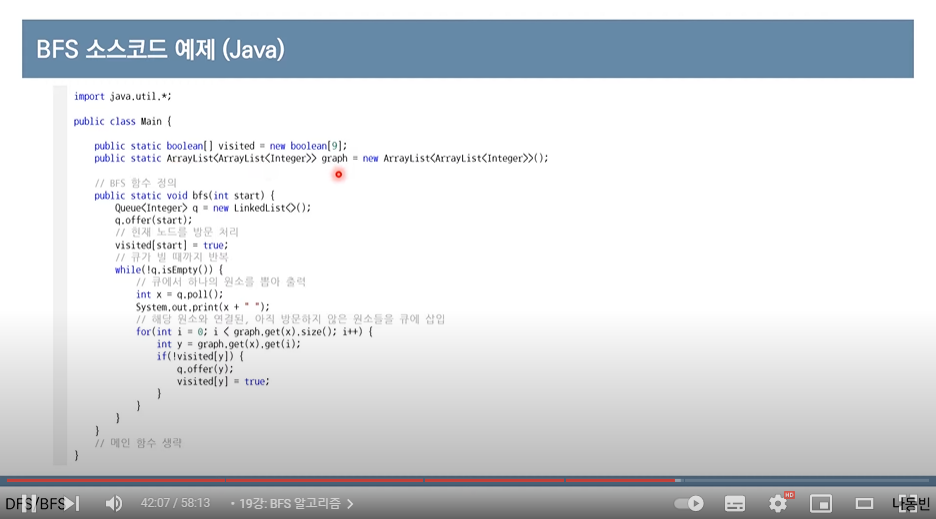
= 너비 우선 탐색. 큐 자료구조를 사용
= 간선의 비용이 모두 같을 때 최단거리 찾고자한다면 BFS 사용한다.
- 탐색 시작 노드를 큐에 삽입하고 방문처리한다.
- 큐에서 노드 꺼낸 뒤에 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리한다.
- 더이상 2번의 과정을 수행할 수 없을 때까지 반복한다.
그래프(=노드와 간선으로 이루어진 자료구조)를 탐색하는 방법인 DFS/ BFS
DFS
1. 모든 노드를 방문하고자 하는 경우에 이 방법을 택한다.
2. DFS가 BFS보다 좀 더 간단하다.
3. 검색 속도 자체는 BFS보다 느리다.
BFS
1. 두 노드 사이의 최단 경로를 찾고 싶을 때 선택한다.
문제 유형에 따른 분류
-
그래프의 모든 정점을 방문하는 것이 주요한 문제
-> DFS, BFS 아무거나 -
경로의 특징을 저장해둬야하는 문제 (ex. 경로에 같은 숫자가 있으면 안된다는 등 각각의 경로마다 특징을 저장해둬야하는 경우(
->DFS
3.최단거리를 구해야하는 문제
-> BFS (너비 우선 탐색으로 현재 노드에서 가까운 곳부터 찾기 때문에)
-
검색 대상 그래프가 정말 크다면 DFS
-
검색 대상의 규모가 크지 않고 검색 시작 지저믕로부터 원하는 대상이 별로 멀지 않다면 BFS
