4주차 : 정렬

참조

숫자의 순서나 어휘의 순서대로 정렬하는 문제인데, 여기서는 이것을 얼마나 효과적으로 해결할 수 있느냐가 핵심이 된다. 데이터를 정렬해야하는 이유는 탐색을 위해서이다. 탐색 대상 데이터가 정렬되어 있지 않다면, 순차 탐색 이외에 다른 알고리즘을 사용할 수 없지만, 데이터가 정렬되어 있다면 '이진 탐색'이라는 강력한 알고리즘을 사용할 수 있다. 삽입과 삭제가 자주 되는 자료의 경우 정렬에 더 많은 시간이 들어가므로 순차 탐색을 하는 경우도 있지만 대부분의 경우 삽입 및 삭제보다는 데이터를 조회하는 것이 압도적으로 많고 조회에 필요한 것이 바로 검색이다.

이진탐색 알고리즘이란 최악의 경우라도 log n의 성능을 보인다.

주어진 데이터들이 있으면 값들을 서로 비교하여 순서에 맞게 자리를 바꿔주는 형태로 정렬을 하는데, 이를 '비교정렬'이라고 부른다. 일반적으로 많이 쓰이는 정렬 방법이고 만들기도 굉장히 쉽다.

대표적인 정렬의 종류

O(n^2)

1) 버블 정렬
1번쨰와 2번째 원소를 비교해서 정렬하고, 2번째와 3번째를 비교하고.. n-1번째와 n번째를 정렬한 뒤 다시 처음으로 돌아가 n-2번째와 n-1번쨰까지 해서 최대 (n*(n-1)/2)번 정렬한다. 하지만 크게 의미는 없는 방법

2) 선택 정렬
1번째부터 끝까지 훑어서 가장 작은게 1번째, 2부터 끝까지 훑어서 젤 작은게 2번째.. 해서 n-1번 반복하는 방법이다.
이중 선택 정렬도 존재하는데, 끝까지 훑어서 최솟값과 최댓값을 동시에 찾아낸뒤 변경하는, 양쪽으로 범위를 한칸씩 줄여서 반복하는 방식이다.

3) 삽입 정렬

k번째 원소를 1부터 k-1까지와 비교해 적절한 위치에 끼워넣고 그 뒤의 자료를 한 칸씩 뒤로 밀어내는 방식. 근데 작은게 뒤쪽에 몰려있으면 아주 힘든 상황이 만들어진다. 하지만 이미 정렬되어 있는 자료구조에 자료를 하나씩 삽입 or 제거하는 경우에는 아주 효율적이며, 배열이 작을 경우에도 효율적이다.

O(n log n)

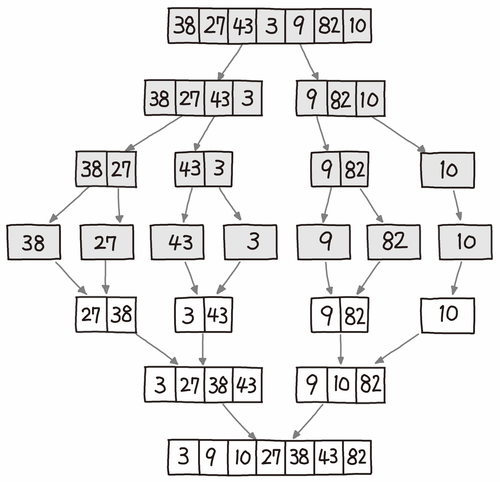
1) 병합 정렬, 합병 정렬

원소개수가 1 또는 0이 될 때까지 두 부분으로 쪼개고 쪼개서 자른 순서의 역순으로 크기를 비교해 병합해나간다.

2) 힙 정렬
원소들을 전부 힙에 삽입한다 -> 힙의 루트에 있는 값은 남은 수들 중에서 최솟값(혹은 최댓값)을 가지므로 루트를 출력하고 힙에서 제거한다. -> 힙이 빌 때까지의 과정을 반복한다.

3) 퀵 정렬
평균적인 상황에서 최고의 성능을 나타낸다.