7주차 : 최단경로 문제1

✔ BOJ_11403

해당 알고리즘 이해를 위해서 블로그 검색을 통해 풀었습니다 :( 참조 코드는 다음과 같습니다. 참조코드

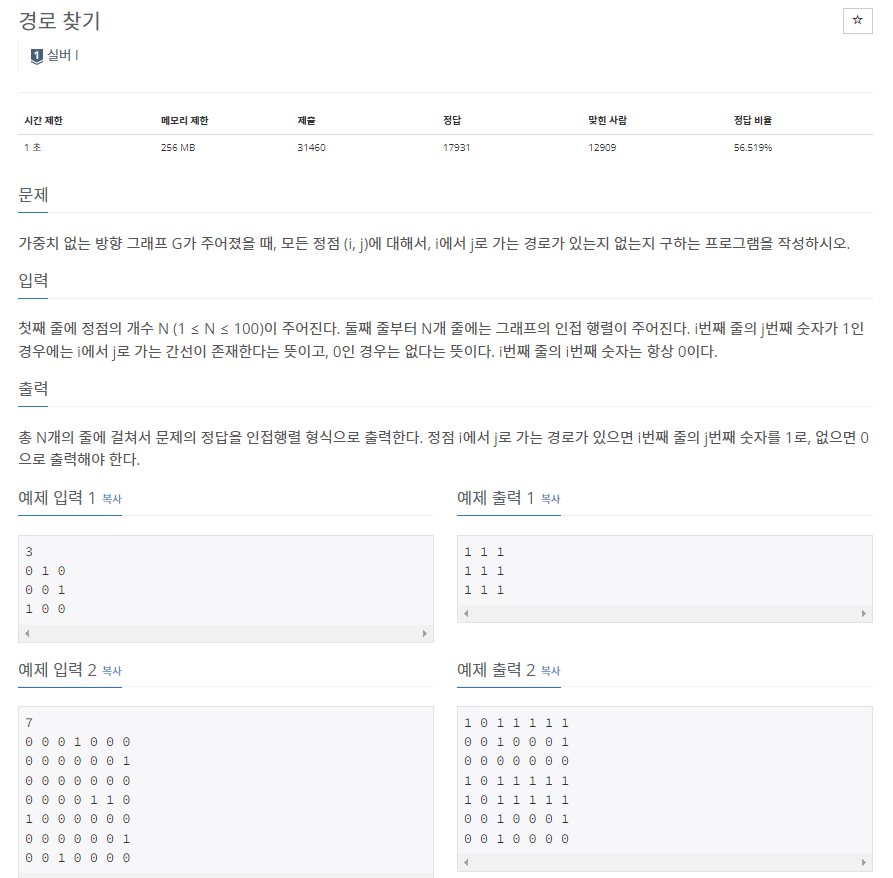
해당 문제는 '플로이드 와샬 알고리즘'을 사용한다. n의 범위가 100 이하이므로 O(N^3)을 사용할 수 있다.

'플로이드 와샬 알고리즘'이란 모든 정점에서 모든 정점으로의 최단 거리를 구하는 알고리즘으로서 거쳐가는 정점 을 기준으로 한다는 것이 특징이다. 즉, i에서 j까지 가는 것과 i->k->j로 가는 것이 같다는 것입니다. 해당 문제는 i에서 j로 갈 수 있는 경로가 있는지 판단하는 것이므로 합당하다.

import java.io*;
import java.util.StringTokenizer;

public class BOJ_11403 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        // 정점의 개수
        int n = Integer.parseInt(br.readLine());

        // 담을 배열
        int[][] arr =new int[n][n];

        StringTokenizer st ;
        for(int i=0;i<n;i++){
            st = new StringTokenizer(br.readLine());
            for(int j=0;j<n;j++){
                arr[i][j] = Integer.parseInt(st.nextToken());
            }
        }

        // 거쳐가는 노드 중심!
        for(int k=0;k<n;k++){
            for(int i=0;i<n;i++){
                for(int j=0;j<n;j++){
                    if(arr[i][k]==1 && arr[k][j] ==1){
                        arr[i][j] = 1;
                    }
                }
            }
        }
        StringBuilder sb = new StringBuilder();
        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                sb.append(arr[i][j]+" ");
            }
            sb.append("\n");
        }

        bw.write(sb.toString());
        bw.flush();
        bw.close();
        br.close();

    }
}