기본 개념

1. 자기 균형 이진 탐색 트리(Self-Balancing BST)
   1. 이진 탐색 트리: 자신의 왼쪽 서브 트리에는 현재 노드보다 값이 작은 것, 오른쪽 서브 트리에는 값이 큰 것들만 들어감
      1. 평균 O(logn)이지만 균형이 무너질 경우 O(N)까지 시간 증가 할 수 있음
2. rb tree는 삽입, 삭제 동안 트리 모양이 균형 잡히도록 red or black 색상 가짐 --> 검색, 삽입, 삭제 시 worst case에도 모두 o(logn) 보장되는 자료 구조임

조건

1. 모든 노드는 빨간색 혹은 검은색이다.
2. 루트 노드는 검은색이다.
3. 모든 리프 노드(NIL)들은 검은색이다. (NIL : null leaf, 자료를 갖지 않고 트리의 끝을 나타내는 노드)
4. 빨간색 노드의 자식은 검은색이다.
   == No Double Red(빨간색 노드가 연속으로 나올 수 없다)
5. 모든 리프 노드에서 Black Depth는 같다.
   == 리프노드에서 루트 노드까지 가는 경로에서 만나는 검은색 노드의 개수가 같다.

삽입 과정

1. 새로운 노드 삽입 시 항상 빨간색으로 삽입

2. 4번 조건 위배되는 상황 발생(= 빨간색 노드가 연속으로 2번 나타날 수 있음)
   

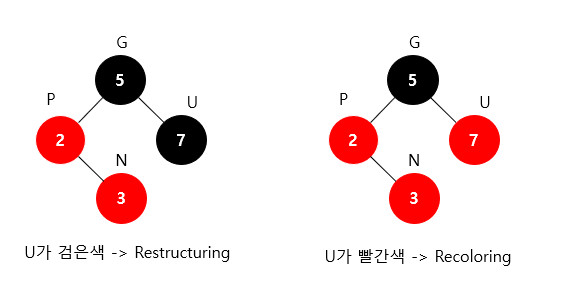
3. 2가지 전략 사용

   1. 삼촌 노드 검은색 --> restructuring
   2. 삼촌 노드 빨간색 --> recoloring

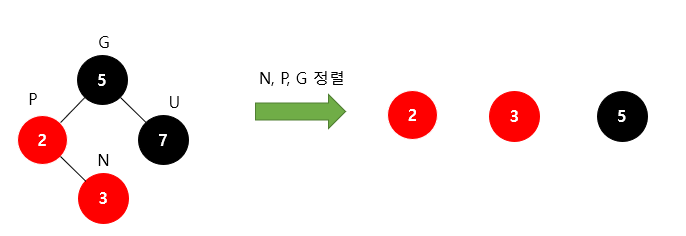
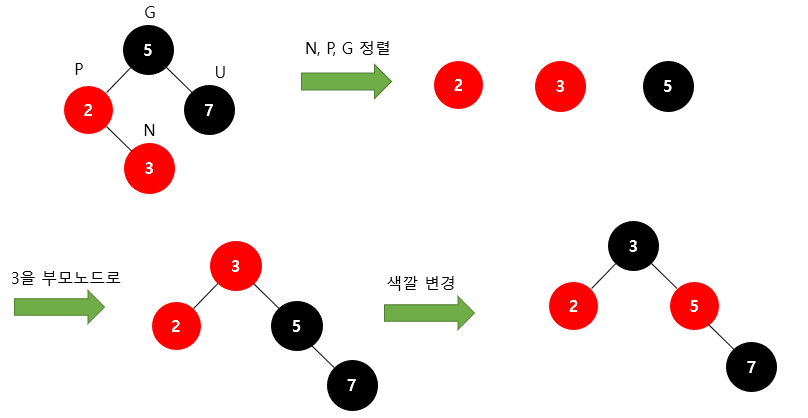
Restructuring

과정
1. 새로운 노드(N), 부모 노드(P), 조상 노드(G)를 오름차순으로 정렬한다.
2. 셋 중 중간값을 부모로 만들고 나머지 둘을 자식으로 만든다.
3. 새로 부모가 된 노드를 검은색으로 만들고 나머지 자식들을 빨간색으로 만든다.

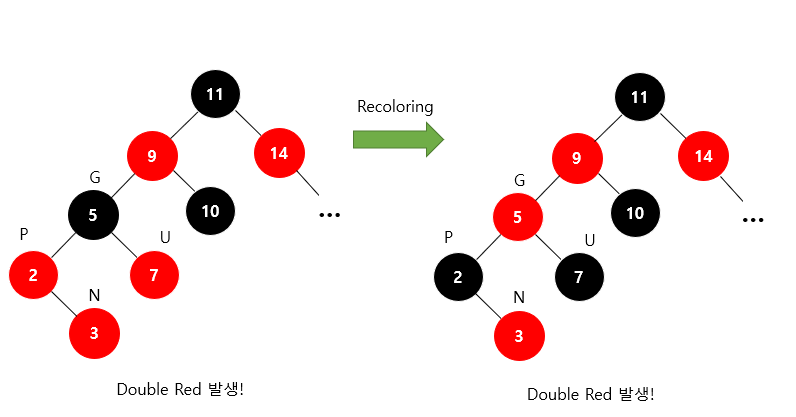
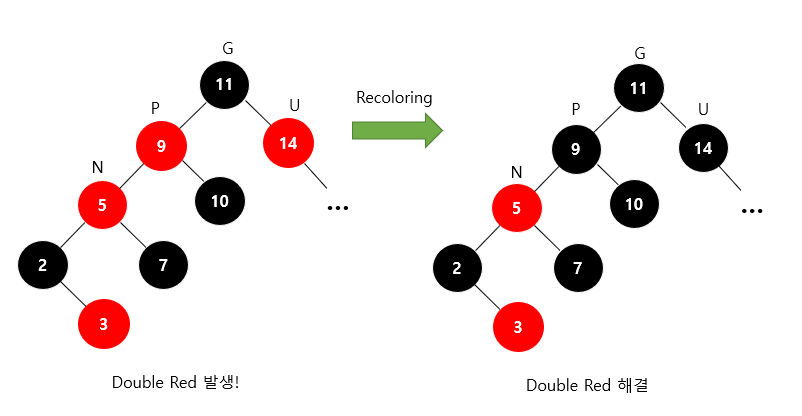
Recoloring

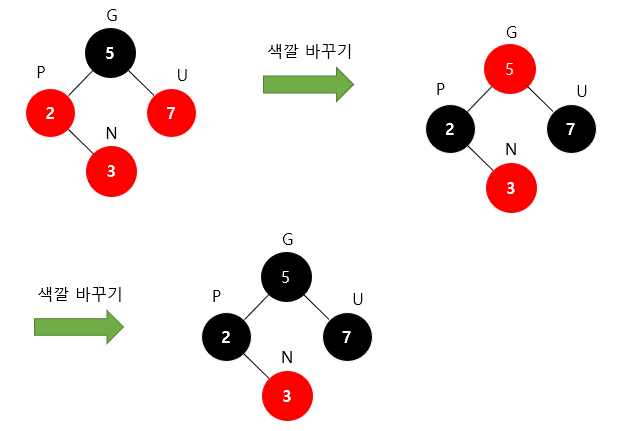
과정
1. 새로운 노드(N)의 부모(P)와 삼촌(U)을 검은색으로 바꾸고 조상(G)을 빨간색으로 바꾼다.
1-1. 조상(G)이 루트 노드라면 검은색으로 바꾼다.
1-2. 조상(G)을 빨간색으로 바꿨을 때 또다시 Double Red가 발생한다면 또다시 Restructuring 혹은 Recoloring을 진행해서 Double Red 문제가 발생하지 않을 때까지 반복한다.

반복 되는 경우