C# 문법 5주차 - 탐색 알고리즘

🔍 탐색 알고리즘(Search Algorithm)

🤔 탐색 알고리즘?

주어진 데이터 집합에서 특정 항목을 찾는 방법을 제공한다.

▪️ 선형 탐색(Linear Search)

• 가장 단순한 탐색 알고리즘. 배열의 각 요소를 하나씩 차례대로 검사하여 원하는 항목을 찾는다.
• 시간 복잡도 : 최악의 경우 O(n)

구현 예제)

• 배열을 처음부터 끝까지 하나씩 비교하여 검색하는 알고리즘
• 배열이 정렬되어 있지 않을 경우 사용

int SequentialSearch(int[] arr, int target)
{
    for (int i = 0; i < arr.Length; i++)
    {
        if (arr[i] == target)
        {
            return i;
        }
    }

    return -1;
}

▪️ 이진 탐색(Binary Search)

• 정렬된 배열에서 빠르게 원하는 항목을 찾는 방법이다. 중간 요소와 찾고자 하는 항목을 비교하여 대상이 중간 요소보다 작으면 왼쪽, 크면 오른쪽을 탐색한다.
• 시간 복잡도 : 최악의 경우 O(log n)

구현 예제)

• 배열이 정렬되어 있을 경우 사용하는 알고리즘
• 중앙값과 비교하여 탐색 범위를 반으로 줄이는 방법으로 빠른 검색이 가능하다!

int BinarySearch(int[] arr, int target)
{
    int left = 0;
    int right = arr.Length - 1;

    while (left <= right)
    {
        int mid = (left + right) / 2;

        if (arr[mid] == target)
        {
            return mid;
        }
        else if (arr[mid] < target)
        {
            left = mid + 1;
        }
        else
        {
            right = mid - 1;
        }
    }

    return -1;
}

📈 그래프(Graph)

▪️ 그래프 개념과 종류

• 정점(Vertex)과 간선(Edge)으로 이루어진 자료 구조
• 방향 그래프(Directed Graph)와 무방향 그래프(Undirected Graph)로 나뉨
• 가중치 그래프(Weighted Graph)는 간선에 가중치가 있다.

▪️ 그래프 탐색 방법

• 깊이 우선 탐색(DFS)

  • DFS는 트리나 그래프를 탐색하는 알고리즘 중 하나로, 루트에서 시작하여 가능한 깊이 들어가서 노드를 탐색, 더 이상 방문할 노드가 없으면 이전 노드로 돌아가는 방식이다.
  • 시간 복잡도 : 최악의 경우 O(V + E)이다. (V는 노드 수, E는 간선 수)

• 너비 우선 탐색(BFS)

  • BFS는 트리나 그래프를 탐색하는 알고리즘 중 하나로, 루트에서 시작하여 가까운 노드부터 방문, 그 다음 레벨의 노드를 방문하는 방식이다.
  • 시간 복잡도 : 최악의 경우 O(V + E)이다. (V는 노드 수, E는 간선 수)

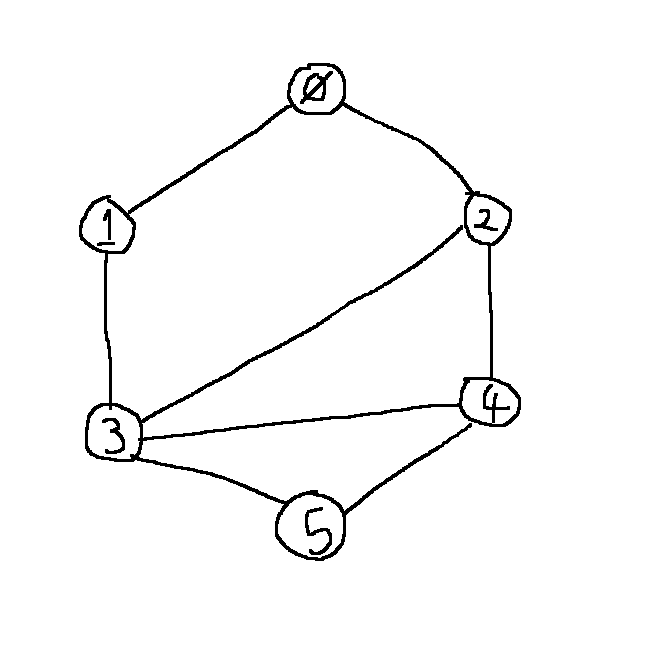
이런 그래프를 탐색한다고 가정해보자!

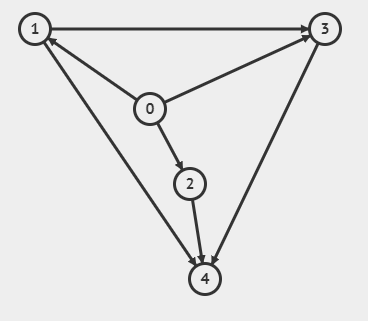
• DFS의 경우

  

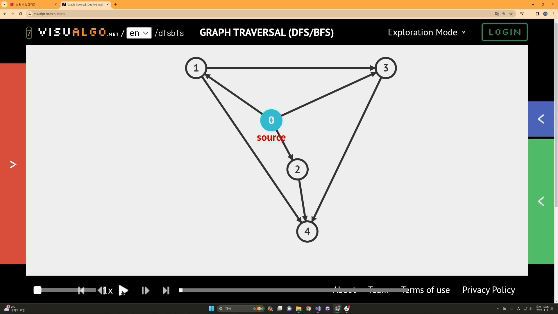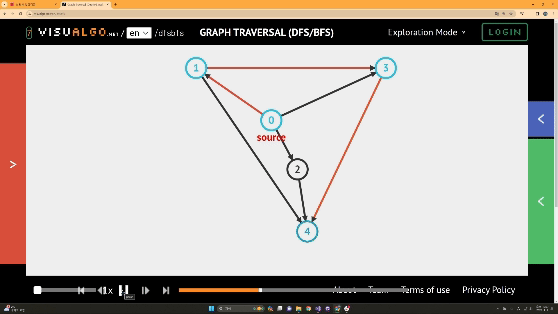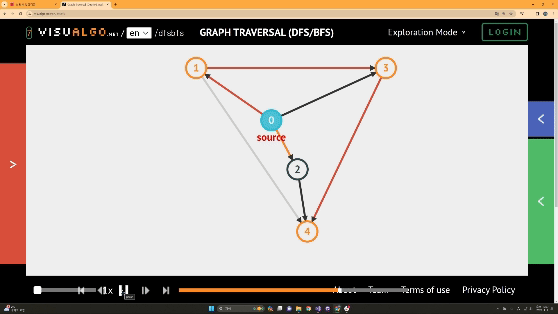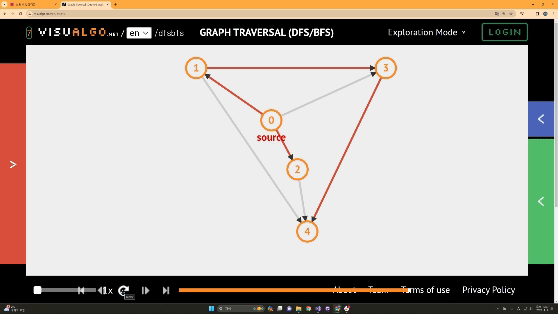
• BFS의 경우

  

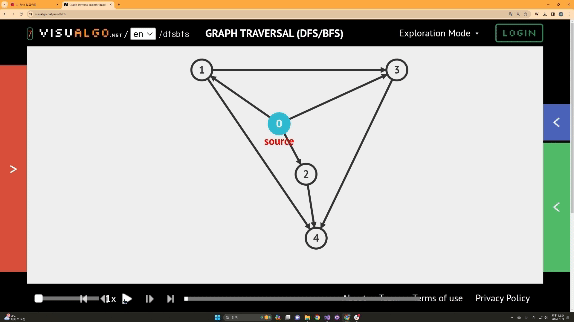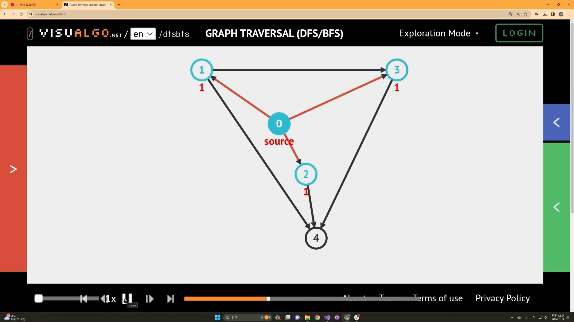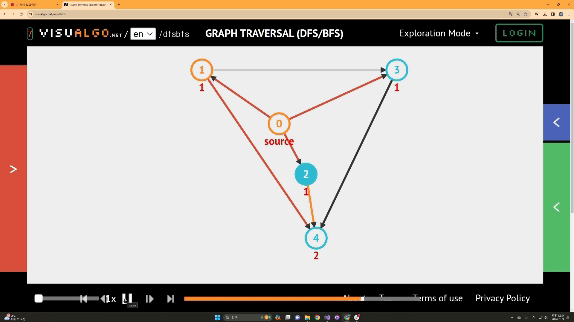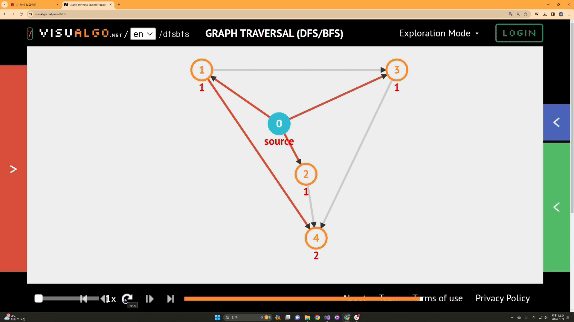
활용 예제)

using System;
using System.Collections.Generic;

public class Graph
{
    private int V; // 그래프의 정점 개수
    private List<int>[] adj; // 인접 리스트

    public Graph(int v)
    {
        V = v;
        adj = new List<int>[V];
        for (int i = 0; i < V; i++)
        {
            adj[i] = new List<int>();
        }
    }

	// 간선 추가
    public void AddEdge(int v, int w)
    {
        adj[v].Add(w);
    }

    public void DFS(int v)
    {
        bool[] visited = new bool[V];
        DFSUtil(v, visited);
    }

    private void DFSUtil(int v, bool[] visited)
    {
        visited[v] = true;
        Console.Write($"{v} ");

        foreach (int n in adj[v])
        {
            if (!visited[n])
            {
                DFSUtil(n, visited);
            }
        }
    }

    public void BFS(int v)
    {
        bool[] visited = new bool[V];
        Queue<int> queue = new Queue<int>();

        visited[v] = true;
        queue.Enqueue(v);

        while (queue.Count > 0)
        {
            int n = queue.Dequeue();
            Console.Write($"{n} ");

            foreach (int m in adj[n])
            {
                if (!visited[m])
                {
                    visited[m] = true;
                    queue.Enqueue(m);
                }
            }
        }
    }
}

public class Program
{
    public static void Main()
    {
        Graph graph = new Graph(6);

		// 그래프 생성
        graph.AddEdge(0, 1);
        graph.AddEdge(0, 2);
        graph.AddEdge(1, 3);
        graph.AddEdge(2, 3);
        graph.AddEdge(2, 4);
        graph.AddEdge(3, 4);
        graph.AddEdge(3, 5);
        graph.AddEdge(4, 5);

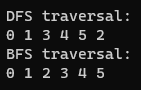
        Console.WriteLine("DFS traversal:");
        graph.DFS(0);
        Console.WriteLine();

        Console.WriteLine("BFS traversal:");
        graph.BFS(0);
        Console.WriteLine();
    }
}

🔍 최단 경로 알고리즘(Shortes Path Problem)

▪️ 최단 경로 알고리즘 개념과 종류

• 다익스트라 알고리즘(Dijkstra Algorithm)
  하나의 시작 점점에서 다른 모든 정점까지의 최단 경로를 찾는 알고리즘. 음의 가중치를 갖는 간선이 없는 경우 사용된다.
• 벨만-포드 알고리즘(Bellman-Ford Algorithm)
  음의 가중치를 갖는 간선이 있는 그래프에서도 사용할 수 있는 최단 경로 알고리즘. 음수 사이클이 있는 경우에도 탐지할 수 있다.
• A* 알고리즘(A-star Algorithm)
  특정 목적지까지의 최단 경로를 찾는 알고리즘. 휴리스틱 함수를 사용하여 각 정점까지의 예상 비용을 계산, 가장 낮은 예상 비용을 가진 정점을 선택하여 탐색한다.

다익스트라 알고리즘 예시)

using System;

class DijkstraExample
{
    static int V = 6; // 정점의 수

    // 주어진 그래프의 최단 경로를 찾는 다익스트라 알고리즘
    static void Dijkstra(int[,] graph, int start)
    {
        int[] distance = new int[V]; // 시작 정점으로부터의 거리 배열
        bool[] visited = new bool[V]; // 방문 여부 배열

        // 거리 배열 초기화
        for (int i = 0; i < V; i++)
        {
            distance[i] = int.MaxValue;
        }

        distance[start] = 0; // 시작 정점의 거리는 0

        // 모든 정점을 방문할 때까지 반복
        for (int count = 0; count < V - 1; count++)
        {
            // 현재 방문하지 않은 정점들 중에서 최소 거리를 가진 정점을 찾음
            int minDistance = int.MaxValue;
            int minIndex = -1;

            for (int v = 0; v < V; v++)
            {
                if (!visited[v] && distance[v] <= minDistance)
                {
                    minDistance = distance[v];
                    minIndex = v;
                }
            }

            // 최소 거리를 가진 정점을 방문 처리
            visited[minIndex] = true;

            // 최소 거리를 가진 정점과 인접한 정점들의 거리 업데이트
            for (int v = 0; v < V; v++)
            {
                if (!visited[v] && graph[minIndex, v] != 0 && distance[minIndex] != int.MaxValue && distance[minIndex] + graph[minIndex, v] < distance[v])
                {
                    distance[v] = distance[minIndex] + graph[minIndex, v];
                }
            }
        }

        // 최단 경로 출력
        Console.WriteLine("정점\t거리");
        for (int i = 0; i < V; i++)
        {
            Console.WriteLine($"{i}\t{distance[i]}");
        }
    }

    static void Main(string[] args)
    {
        int[,] graph = {
            { 0, 4, 0, 0, 0, 0 },
            { 4, 0, 8, 0, 0, 0 },
            { 0, 8, 0, 7, 0, 4 },
            { 0, 0, 7, 0, 9, 14 },
            { 0, 0, 0, 9, 0, 10 },
            { 0, 0, 4, 14, 10, 0 }
        };

        int start = 0; // 시작 정점

        Dijkstra(graph, start);
    }
}