단순 선형 회귀
단순 선형 회귀란 단 하나의 특성(feature)을 가지고 타깃을 예측하기 위한 회귀 모델을 찾는 것이다
둘 이상의 특성이 사용된다면 다중 선형 회귀 라고 한다.
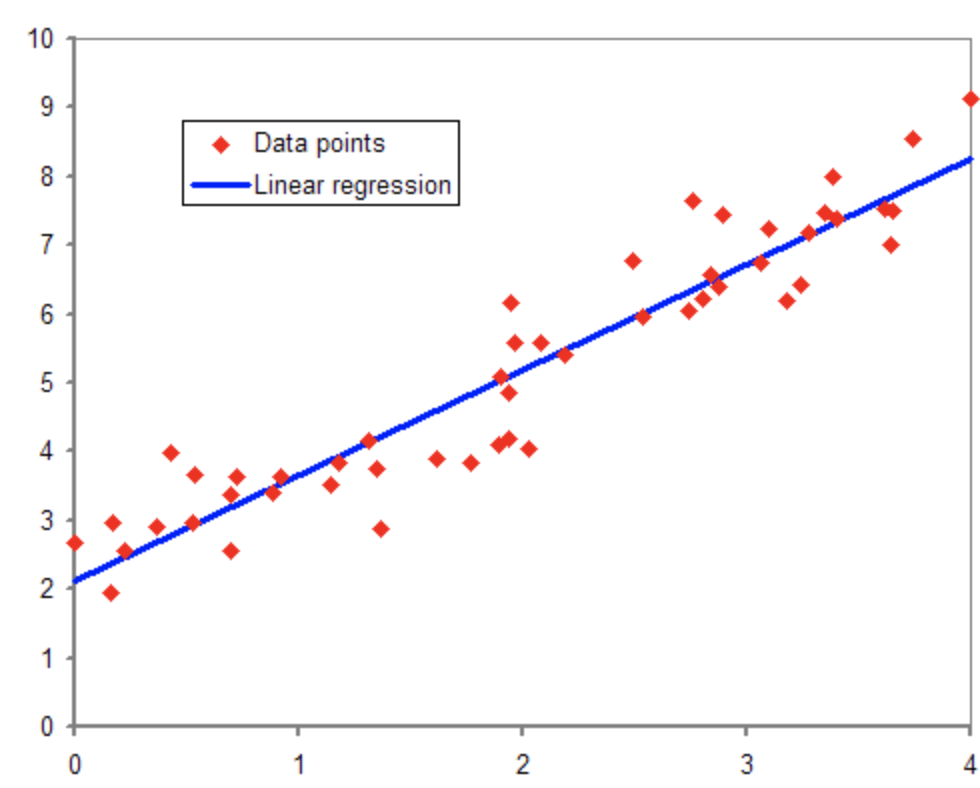
위의 빨간 점은 샘플(sample)이다. x 좌표 값은 샘플의 특성값을 의미하고 y 좌표 값은 타깃(혹은 라벨 값)을 의미한다. 쉽게 말해 샘플의 특성값을 이용해 특성과 타깃의 관계를 가장 잘 설명하는, 타깃과 가장 일치하는 직선을 찾는 과정이라고 생각하면 된다. 주어진 데이터에 완벽하게 대응하는 선형 함수를 찾아내는 것은 거의 불가능하고, 최대한 특성과 타깃 값이 가장 잘 들어맞는 일차 함수 식을 찾아내는 것이 단순 선형 회귀의 목적이다.
예측 함수
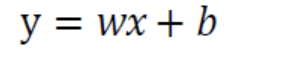
x는 특성, y는 예측 값이다. w는 기울기, b는 y절편을 뜻하지만 w는 가중치(weight), b는 offset으로 부르는 것이 적절하다. 선형 회귀에서는 여러 샘플의 특성 값과 예측 값을 활용해 가장 적절한 w와 b를 구하는 것이 목적이다.
평균 제곱 오차 (Mean Square Error)
선형 회귀에서는 목적 함수(또는 비용 함수)로 평균 제곱 오차를 사용한다. 여기서 목적 함수란 샘플 데이터와 타깃과의 유사도를 의미하며 목적 함수가 최소가 되도록 파라미터를 학습시킨다.
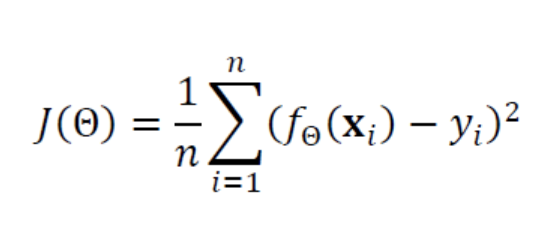
f(x)는 위의 예측 함수이고, y는 타깃 값을 의미한다. 예측 값에서 타깃 값을 뺀 오차를 샘플 개수로 나누어 오차도를 구한다.
구현 코드
import numpy as np
x_train = np.array([1., 2., 3., 4., 5., 6.])
y_train = np.array([9., 12., 15., 18., 21., 24.])샘플 값은 [1, 2, 3, 4, 5, 6] 타깃 값은 [9, 12, 15, 18, 21, 24]로 정의한다.
이 경우 학습이 완료됐을 때 W와 b는 각각 3, 6이 되어야 한다.
W = 0.0
b = 0.0초기의 가중치와 offset은 대부분 random 값으로 초기화 하지만 지금은 0으로 초기화한다.
n_data = len(x_train) # 6
epochs = 5000
learning_rate = 0.01epoch은 전체 데이터 셋에 대해 한 번 학습을 하는 사이클을 의미한다.
learning rate는 경사하강법을 사용할 때 파라미터 업데이트의 가중치를 의미하며 learning rate는 학습속도와 예측 정확도에 영향을 미치므로 적절히 설정해야 한다.
for i in range(epochs):
hypothesis = x_train * W + b
cost = np.sum((hypothesis - y_train) ** 2) / n_data
hypothesis : 예측 함수
cost : 목적(비용) 함수, 평균 제곱 오차
gradient_w = np.sum((W * x_train - y_train + b) * 2 * x_train) / n_data
gradient_b = np.sum((W * x_train - y_train + b) * 2) / n_data
W -= learning_rate * gradient_w
b -= learning_rate * gradient_bgradient_w는 목적 함수인 평균 제곱 오차를 W에 대해 편미분해 계산한 값이며 경사하강법을 적용해 다음 W를 학습률과 곱해 업데이트한다.
마찬가지로 gradient_b는 b에 대한 편미분 계산값이다.
전체 코드 및 실행
import numpy as np
x_train = np.array([1., 2., 3., 4., 5., 6.])
y_train = np.array([9., 16., 23., 30., 37., 44.])
W = 0.0
b = 0.0
n_data = len(x_train)
epochs = 5000
learning_rate = 0.01
for i in range(epochs):
hypothesis = x_train * W + b
cost = np.sum((hypothesis - y_train) ** 2) / n_data
gradient_w = np.sum((W * x_train - y_train + b) * 2 * x_train) / n_data
gradient_b = np.sum((W * x_train - y_train + b) * 2) / n_data
W -= learning_rate * gradient_w
b -= learning_rate * gradient_b
if i % 100 == 0:
print('Epoch ({:10d}/{:10d}) cost: {:10f}, W: {:10f}, b:{:10f}'.format(i, epochs, cost, W, b))
print('W: {:10f}'.format(W))
print('b: {:10f}'.format(b))
print('result : ')
print(x_train * W + b)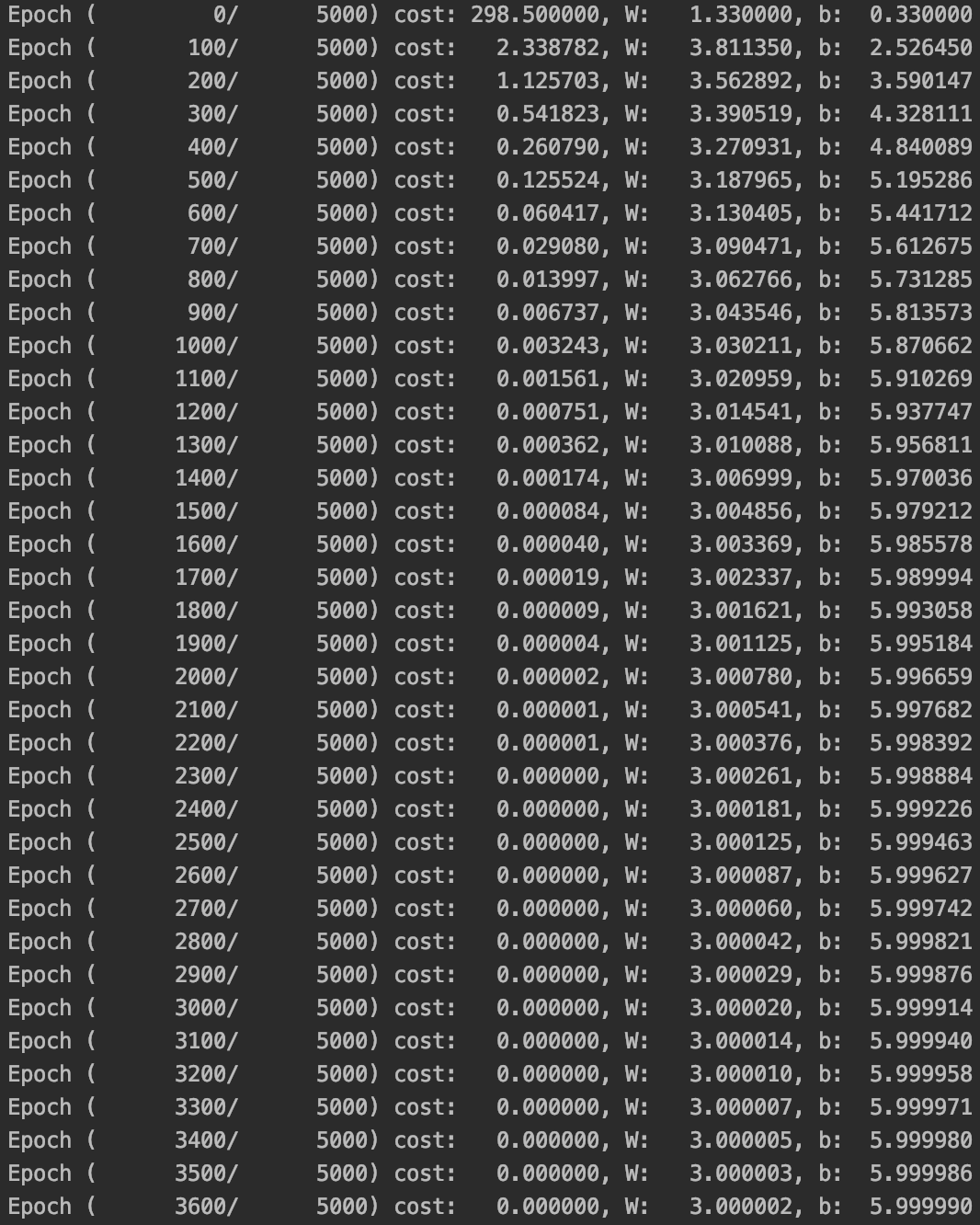
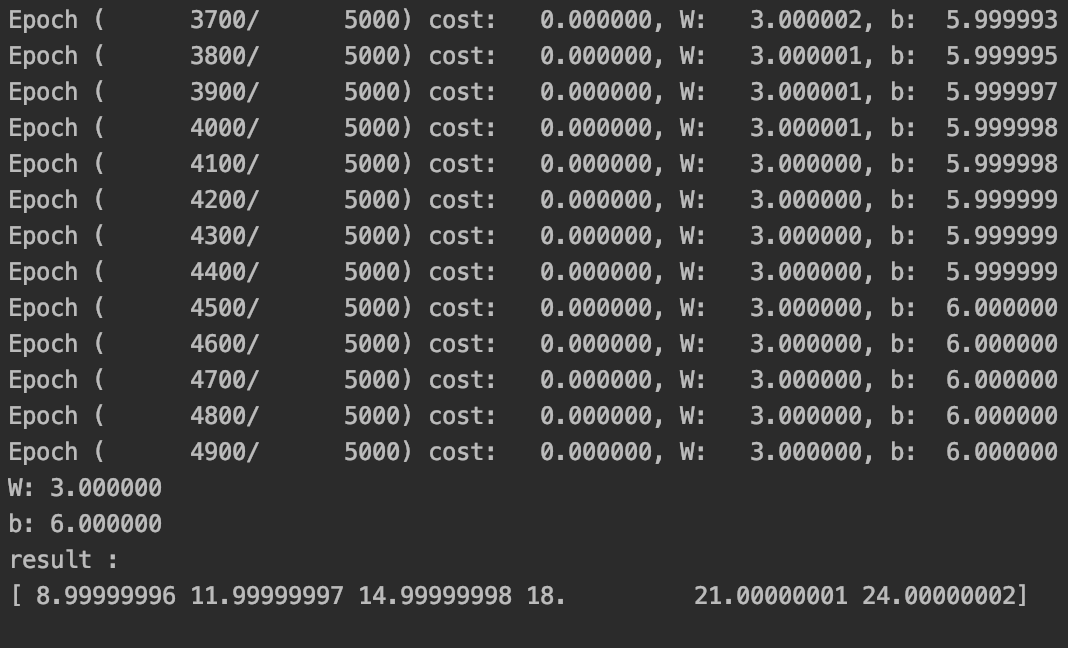
학습을 진행하며 W와 b가 각각 3, 6에 가까워짐을 볼 수 있다.

...👏👏👏