Enhancing the Locality and Breaking the Memory Bottleneck of Transformer on Time Series Forecasting 정리

경근·2023년 2월 1일

논문 정리

목록 보기

7/7

Abstract

시계열을 예측하는데 있어서 트랜스포머의 문제점을 다룸
1. Locality - agnostics : 닷프로덕트 연산의 셀프어텐션 메카니즘은 local context을 잘 담지 못함
2. memory bottleneck : $L^2$ 에 비례하기 때문에 시계열이 길면 메모리 복잡도 증대

이 이슈를 해결하기 위해 convolutional self-attention 제시
: causal convolution으로 causal convolution 을 쿼리와 키를 제공하며 local context를 더 잘 학습함
즉, LogSparseTransformer 를 propose 하는데, 이는 $O(L(logL)^2)$ 메모리 코스트를 요구하며 시계열의 세분성과 long-term dependency를 잘 학습함

Introduction

트랜스포머가 어텐션 메커니즘을 이용하여 RNN과는 다르게 포지션에 무관하게 패턴을 포착할 수 있었음. 그러나 기존의 닷프로덕트 연산은 Local context에는 민감하지 못했는데, 모델의 최적화 이슈에서 자유롭지 못했음. 또한, 메모리 복잡도가 시퀀스 길이의 제곱에 비례하므로, 긴 시계열에서는 활용하기 어려웠음. 따라서 우리의 컨트리뷰션은 다음과 같이 3가지임

트랜스포머 아키텍처를 시계열 예측 분야에 apply 하여 기존 RNN 기반의 모델보다 롱텀 디펜더시의 학습이 원활함을 검증함
convolutional self-attention 을 제시하는데, 이는 causal convolution을 진행하여 self-attention layer의 쿼리와 키를 매칭하는 것이다. 이를 통해 모델을 낮은 학습 로스로 시계열 정확도를 높임
LogSparse Transformer 를 제시하여 $O(L(logL)^2)$ 의 메모리 코스트로 메모리 보틀넥을 없앤다. 또한 기존 트랜스포머보다 적은 메모리 사용으로도 더 좋은 결과를 나타낸다.

Arima & Box-Jenkins method : linear 하다는 가정과 제한된 scalability 때문에 large-scale forecasting에 적합하지 않음.
Hierarchical Bayesian method : 다변량 시계열을 그래프를 통해 해석
AR을 RNN과 결합하여 encoder-decoder의 분포 확률을 학습함
RNN을 인코더로 사용하고, MLP를 통해 error accumulation 이슈를 해결하고 multi-ahead forecasting 진행
Global RNN을 사용하여 각 시계열에 linear SSM의 파라미터를 출력하여 비선형 다이나믹스를 로칼로 리니어하게 예측함
local Gaussian process의 노이즈를 이용하여 global RNN이 패턴을 공유하도록 함
AR 모델과 SSM의 이점을 합치고, 복잡한 latent 공간 프로세스를 유지하여 multi-step 예측을 평행하게 진행
Transformer가 최근 propose 되어 sequence modeling에 좋은 효과를 보였다. 번역, Speech, 음악과 이미지 생성에 사용되었다. 그러나, 아주 긴 sequence에 대해서는 스케일링 문제가 생기게 된다. 제곱으로 어텐션 계산량이 올라가기 때문에 문제인데, 시계열이 strong long-term 및 fine granularity 에 대한 의존도가 클 때 문제가 된다.

Backgrounds

문제 정의 :
N개의 단변량 시계열 데이터가 있다고 가정하면, 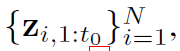의 꼴로 나타남

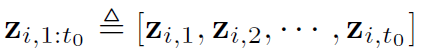
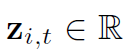
우리는 다음 타우 스텝을 예측할 것이다.

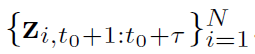
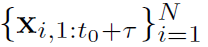
$X_i$ : d차원의 시간기반의 공분산 벡터로 전체 time period 에서 known 되어 있다고 알려져 있음. 예를 들어, week의 day, day의 hour
즉, 우리는 조건부 확률 분포를 모델하는 것이 목표이다.

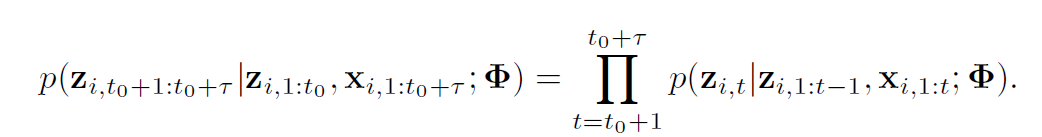
$\phi$ : 시계열들의 collection에서 learnable parameter를 의미

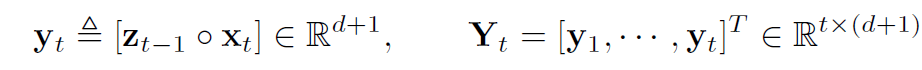
observation과 공분산을 활용하기 위해 augmentation 행렬을 concat 을 통해 획득함
$Y_t$ 가 주어졌을 때 $z_t$ 의 distribution을 예측하기 위해 $f(Y_t)$ 를 구하는 것이 중요하다

트랜스포머:
우리는 위 $f(Y_t)$ 에서 $f$ 를 트랜스포머의 멀티헤드 셀프 어텐션 메카니즘을 활용함. 트랜스포머는 롱텀, 숏텀의 dependencies를 학습하므로, 다른 attention head가 다른 패턴을 학습하는데 도움을 준다.
리니어 프로젝션을 통해 스케일된 닷프로덕트 어텐션은 벡터 아웃풋을 다음과 같이 계산함

M은 마스크됨 매트릭스이다. upper triangular elements를 $-\infty$ 로 두어 future information의 leakage를 방지한다. $O_1, O_2, ..., O_H$ 를 concat하고 선형 프로젝션을 한번 더 한다. Attention output 다음, 피드포워도 서브레이어와 2개의 fc 네트워크, ReLU 활성화를 거치게 된다.

Methodology

4.1 Enhencing the locality of Transformer

시계열의 패턴들은 다양한 이벤트로 인해 시간에 따라 변동이 큼. 기존 트랜스포머의 self-attention layer는 쿼리와 키의 유사도를 point-wise value로 계산되었는데 이는 shape과 같은 local context를 사용하지 않은 방법이다.

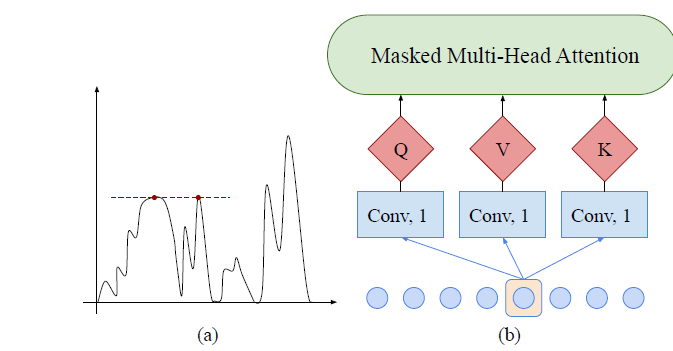
Fig.1 에서 a와 b를 보면 근처 local context의 고려 없이 두 점과의 유사도를 측정하게 된다.
Local context에 상관 없이 query 와 key 값을 단순히 매칭하는 것은 self-attention 모듈을 confuse 하게 할 것이다. 특히, 관측된 데이터가 anomaly인지, change 포인트인지, 패턴의 부분인지가 문제이며 또한 기초적인 최적화 이슈까지 가져올 것이다.
따라서, 우리는 convolutional self-attention 을 각 이슈에 사용한다.

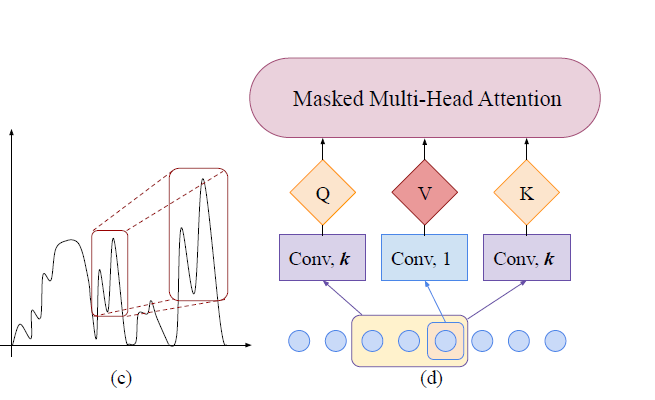
기존의 트랜스포머와 다른 점은, stride 1 & kernel size K 의 convolution layers를 사용하여 인풋을 쿼리와 키로 변환함. 따라서, locality awareness가 이루어지며 이를 통해 더 relevant features 를 shape matching 을 통해 이룰 수 있다.
기존의 kernel size 1과 stride 1 사이즈(matrix multiplication)과는 다른 방법론을 사용하게 된다. causal convolutions는 현재의 포지션이 future information을 참조할 수 없도록 해야 한다. causal convolution을 사용함으로써, 만들어진 쿼리와 키는 local context에 더 집중할 수 있으며 그러므로 그들의 similarities를 local shapes을 통해 계산할 수 있게 된다. 이는 더 정확한 예측이 가능하도록 한다. 단지, 커널 사이즈가 1이 되면, 기존의 트랜스포머의 셀프어텐션 메커니즘과 동일해지기 때문에 generalization으로 보이게 된다.

4.2 Breaking the memory bottleneck of Transformer

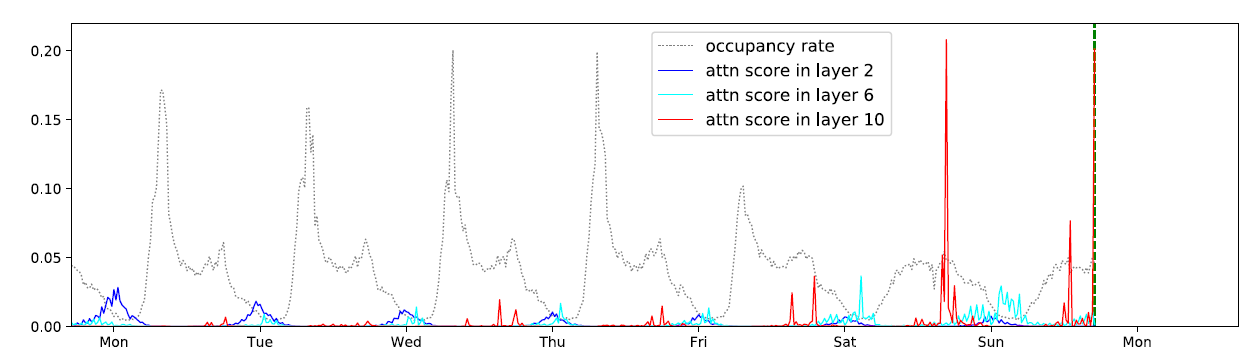
우리의 접근론을 검증하기 위해 학습된 어텐션 패턴 평가를 traffic-f데이터셋에 대해 진행하였다. traffic-f 데이터셋은 샌프란시스코 베이에어리어의 20분 마다의 963개의 자동차 차선의 점유율을 나타낸다. 첫번째로, 10 laye의 full-attention으로 학습을 진행하여 패턴을 나타냄. Layer2는 global patterns을 잘 나타냈지만, Layer6와 10은 pattern-dependent sparsity만을 나타내며 이는 몇몇 sparsity의 도입은 퍼포먼스를 해치지 않는 선에서 도입해도 될 것으로 보인다. 또한, 시퀀스 길이 L에 모든 cell pair를 계산하는 것은 $O(L^2)$ 의 메모리 사용을 요구할 것이다.

LogSparse 트랜스포머를 제안하는데, 단지 $O(logL)$ 의 닷프로덕트 연산을 각 레이어의 셀에 대해 진행한다. 그러므로 우리는 $O(logL)$ 레이어만 쌓아도 모든 cell 의 정보를 엑세스 할 수 있다. 그러므로 최종적인 메모리 사용은 $O(L(logL)^2)$ 이 된다.

우리는 $I_l^k$ 을 정의하는데, $l$ 번째 셀이 $k_{th}$ 레이어에서 $(k+1)_ {th}$ 계산할 때 attend 하는 셀의 인덱스들을 의미한다.

즉, reformer에서 attend 하는 set이라고 보면 된다. 바닐라 트랜스포머에서는 다음과 같았다.

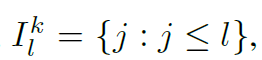
시퀀스 길이 스퀘어에 메모리가 비례하는 이슈에 대응하기 위해 인덱스 서브셋을 다시 정의함

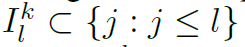
즉, 서브셋을 이전에 메모리 코스트가 원하는대로 증가하기 위해서는 다음과 같이 지수적으로 증가할 필요가 있다.

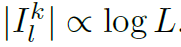
셀 l 은 k번째 self-attention 레이어에서 $I_l^k$ 로 인덱스된 셀들의 weighted 조합이다. 그리고 $I_l^k$ 로 인덱스된 cell들의 정보를 다음 레이어에 pass한다.
$S_l^k$ 는 정보가 $k_{th}$ 레이어에서 셀 l에 정보가 passed 된 인덱스들의 set이다. 모든 셀들은 이전 셀들과 자기자신에게서 정보를 받기 때문에, $\tilde{k_l}$ : stacked layer의 수는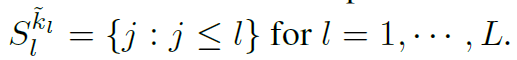
를 만족해야 한다.
즉, $\forall l$ & $\leq$ $l$ 인 경우, $P_{jl}$ = (j, $p_1$ , $p_2$ ..., $l$ ) 인 다이렉트 path가 있게 되고, $\tilde{k_l}$ 의 edge들이 있게 된다.

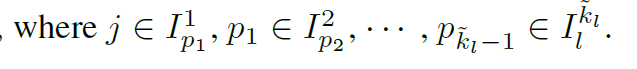
우리는 LogSparce 셀프 어텐션 메카니즘을 제시하여 각 셀들이 이전 셀들만 attend하며, exponential step size를 가지게 한다. $\forall$ $k$ 와 $l$ 에 대해
$I_l^k$ =

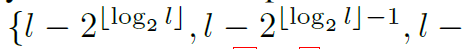
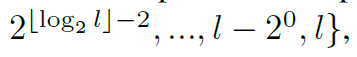
Theorm 1. $\forall$ $l$ , $j$ $\leq$ $l$ 인 것은 만약 | $log_2l$ | + 1 의 레이어를 쌓았다면, 적어도 cell $j$ 에서 cell $l$ 로의 path가 하나는 있다는 것을 의미한다. 게다가, $j$ <1 일 때, $j$ 번째 셀에서 $l$ 번째 셀로 feasible path는

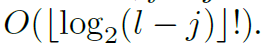
로 증가한다.

즉, Theorm 1 은 각 레이어에서의 메모리 사용이 감소하였음에도, 어떠한 셀의 정보가 다른 어떤 셀로 이동할 수 있음을 보이며, 이는 레이어의 수를 $|log_2L|$ + 1 로 설정하면 된다. 즉, 전체적인 메모리는 $O(L(log_2L)^2$ ) 임을 알 수 있으며, GPU 메모리 제한을 완화할 수 있다. 게다가, 두개의 cells가 분리되기 때문에, paht의 수의 증가는 $log_2(l-j)$ 에 비례한다. 이는 이 방법이 롱텀 디펜던시를 모델링하는데 rich한 방법이라는 것이다.

Local Attention

각 cell이 왼쪽의 윈도우사이즈 $O(log_2L)$ 을 가지는 셀을 attend 하여 더 많은 trend 와 같은 local 정보를 더 잘 활용할 수 있다.

Restart Attention

인풋 시퀀스 전체의 길이가 $L$ 일 때, 이를 나눌 수 있다. $L_{sub}$ 는 $L$ 에 포함되어 있고, 각각 LogSparse attention을 적용한다.

Local attention과 Restart Attention을 적용하는 것은 제시한 sparse attention을 해치지 않으면서 더 많은 path를 만들고, path의 edge 수는 줄인다.

Experiments

5.1 Synthetic datasets

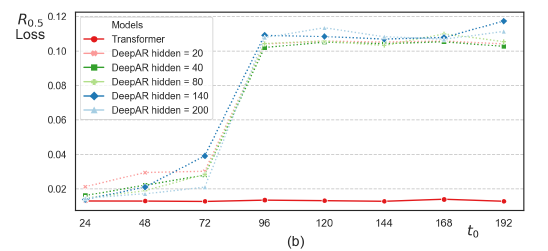
일반 트랜스포머의 long-term dependency 학습의 검증을 위한 실험
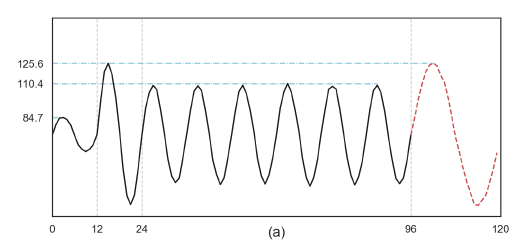
long-term dependency를 학습하기 위해 piece-wise sinusoidal signal을 만들었다.

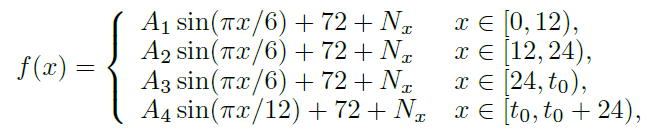
$A_1, A_2, A_3$ 는 [0,60]에서 유니폼 분포이다. $A_4$ = $max(A_1, A_2)$ 이고 $N_x$ 는 정규분포 노이즈이다.
마지막 24스텝을 이전 $t_0$ 포인트가 주어졌을 때 예측함
큰 $t_0$ 일 수록 예측이 더 어려웠는데, $A_1, A_2$ 간의 관계를 학습하기 어려웠기 때문이다. 그러므로, 8개의 다른 데이터셋들을 $t_0$ 값을 바꿔가면서 {24, 48, 72, 96, 120, 144, 168, 192} 를 테스트함
$t_0 = 96$ 은 다음 예제와 같음

Deep AR 과 비교를 진행하였음. 3 layer의 LSTM이고, Deep AR에서 hidden size h를 20, 40, 80, 140, 200 으로 비교
LSTM은 long-term dependency를 잘 캡처하지는 못했지만 트랜스포머는 잘 학습함을 보여줌

5.2 Real-world datasets

electricity-f(fine) 데이터셋 : 370명의 전기 사용 데이터로 15분에 한번씩 샘플링
electricity-c(coarse) 데이터셋 : 4포인트를 하나씩 샘플하였으므로, 1시간에 한번씩 샘플링
traffic-f(fine) 데이터셋 : 963 차선을 20분마다 기록
traffic-c(coarse) 데이터셋 : 같지만 1시간에 한번씩 샘플링함
solar 데이터셋 : solar power 생산량 2006년 1월부터 8월까지, 137개의 PV plant에서 1시간마다 측정
wind 데이터셋 : 28개국의 power plant의 맥시멈 아웃풋 퍼센티지를 나타냄
M4-Hourly : 414시간동안 한 시간마다의 M4 competition을 나타냄
traffic-c 가 electricity-c보다 weekdays와 weekends 에 더 많은 차이를 보이기 때문에 traffic-c 데이터셋이 모델이 long -short term dependency를 잘 더 캡쳐해야 정확하게 나온다.

Long-term and short-term forecasting

베이스라인으로 arima, TRMF, DeepAR, RNN-based(DeepState)
short-term dependency 능력을 보이기 위해 7일동안 매일마다의 예측성능을 단계적으로 검증함
long-term forecasting 을 위해 7일 이후를 바로 예측함

Convolutional self-attention

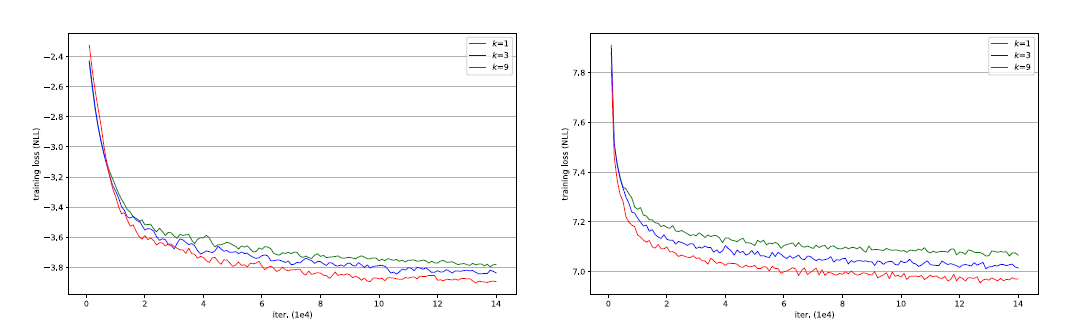
kernel size k 를 {1,2,3,6,9}를 사용하고 다른 세팅은 그대로 고정하였다. 결과는 elec-c 데이터에서 kernel size {2,3,6,9} 를 맞췄을 때 $R_{0.5}$ 에 기존 트랜스포머보다 좋은 성능을 보였음. 이는 elec-c 데이터셋이 challenge가 다른것에 비해 부족하고, 공분산 벡터가 모델에 적용된것이 이미 예측하기에 정보가 충분하다고 예측한다. 그러므로, 더 많은 local context를 인지하는것이 정확도 향상에 영향을 미치지 않는것으로 추정된다. 그러나, traffic-c의 경우에는 kernel size k 가 커질수록 9프로까지 더 향상된 예측 정확도를 보인다. 이 데이터셋의 경우에는 더 많은 local context를 학습하는 경우 더 정확한 결과를 낼 수 있음을 보인다.
또한 local context를 query-key matching 을 통해 학습이 좀 빠르고 수렴이 빠르게 됨을 알 수 있다.
커널사이즈 k {1,3,9}를 통해 수렴 속도에 차이가 있음을 보인다.

Sparse attention

fine-grained dataset에 대해 LogSparse Transformer를 검증함
elec-f 와 traf-f 는 c 데이터에 비해 더 많은 노이즈를 가지고 있다.
1. 메모리 사용량이 같은 경우
elec-f
$L_{e1} = 768$
$L_{e1}/8$ : subsequence length
$log_2(L_{e1}/8)$ : local attention length
$L_{e2} = 293$ : full attention

traf-f
$L_{t1} = 576$
$L_{t1}/8 = 576$ : subsequence length
$log_2(L_{t1}/8)$ : local attention length
$L_{t2} = 254$ : full attention

sparse 및 full attention을 with/without convolutional self-attention

위는 메모리가 같게 sequence 를 넣은 경우

convolutional self-attention 이든 아니든, sparse attention model은 elec-f보다 traf-f에서 더 좋은 결과를 나타냈다.
또한, sparse 와 full attention 모두 convolutional self-attention이 traf-f 에서 더 좋은 성능을 보였다.

sequence 길이가 같은 경우
elec-f
$L_{e1} = 768$
$L_{e1}/8$ : subsequence length
$log_2(L_{e1}/8)$ : local attention length
$L_{e2} = 768$ : full attention

traf-f
$L_{t1} = 576$
$L_{t1}/8 = 576$ : subsequence length
$log_2(L_{t1}/8)$ : local attention length
$L_{t2} = 576$ : full attention

아래가 sequence 길이가 같게 넣은 경우

대부분의 케이스에서 Full attention이 성능이 좋게 된다. 하나의 반례로, traf-f가 아주 강한 long-term dependency를 가지기 때문에, sparse + conv를 같이 진행한 경우 가장 성능이 좋았다.

다른 베이스라인과의 비교를 통해서도 다음과 같이 좋은 성능을 보였음

6. Conclusions

본 연구에서 트랜스포머를 시계열 예측에 사용하였음. 우리의 실험은 트랜스포머가 long-term dependency를 LSTM보다 잘 capture함을 보였음. 또한 real-world dataset에서 convolutional self-attention 을 통해 다른 베이스라인보다 월등함을 보여주었다. 또한 본 연구에서 제시한 방법으로 같은 메모리 budget에도 sparse attention 모델은 더 좋은 결과를 롱텀 디펜던시를 달성할 수 있었다.

경근