Binary (이진)
2가지 전기적 상태만으로도 우리는 중요한 정보를 표현할 수 있다
우리는 이 표현을 문자상으로 '두가지 상태'를 일컫는 이진(Binary) 이라고 부른다.
2가지 상태는 "참"과 "거짓"으로 나타내는 데 필요하다
초기 전자 컴퓨터 중에는 3 개의 상태를 가진 3진법 또는 5진법을 채택한 컴퓨터도 있었다. 그러나 중간 상태가 많을 수록 그것을 나누기가 힘들었다. 트랜지스터가 1초에 수백만 번 상태를 바꾼다면 상황은 더 안 좋다.
그래서 단지 on과 off만을 사용하고 두 개의 신호를 멀리 배치하게 되었다.
컴퓨터 안에서,
on 상태는 전류가 흐르고, true 를 나타내는 상태
off 상태에서 전기는 흐르지 않고, false 상태를 나타낸다
우리는 true와 false를
이진수인 1과 0을 사용해서 나타낼 수 있다
이진법을 채택한 또 다른 이유는 참과 거짓을 다루는 학문이 독점적으로 있었기 때문이다.
그 수학 분야는 참과 거짓을 조작하는데 필요한 규칙과 연산방법을 모두 알아냈다. 이것을 부울대수학이라고 부른다.
Boolean Algebra (부울 대수학)
부울 대수학은 1800년대 영국 수학자 조지 부울George Boole의 이름을 따서 만들었다. 그는 "아래에, 걸쳐서, 기준 밖의" 상태를 나타내는 논리적 표현에 관심이 있었다. 부울의 접근은 논리 방적식을 통해 공식, 체계적으로 증명 되었다.
일반적으로 대수학에서 변수의 값은 숫자이며 연산은 덧셈과 곱셈 같은 것이다. 부울 대수학에서는 변수의 값은 참과 거짓이고 연산은 논리적이다.
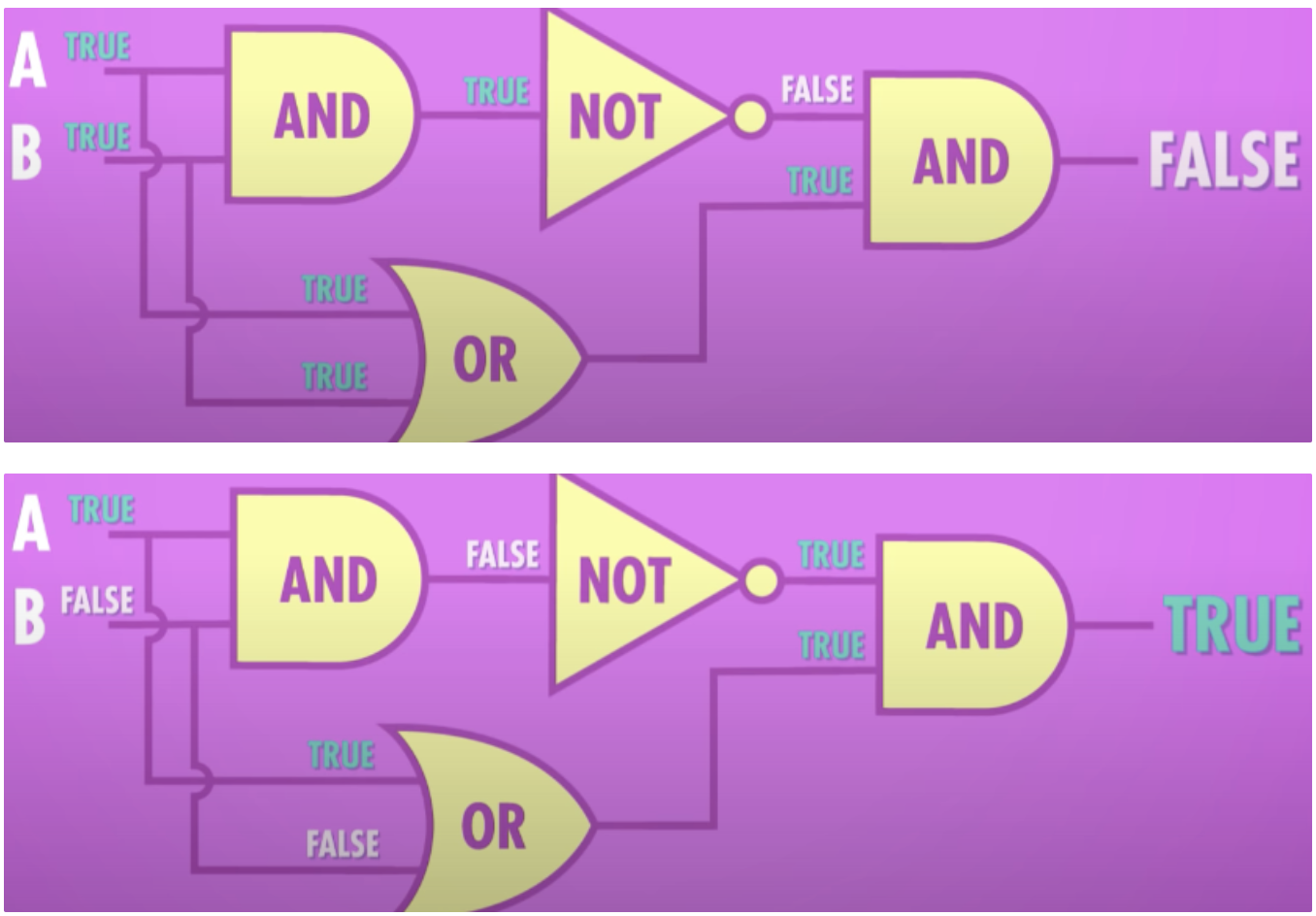
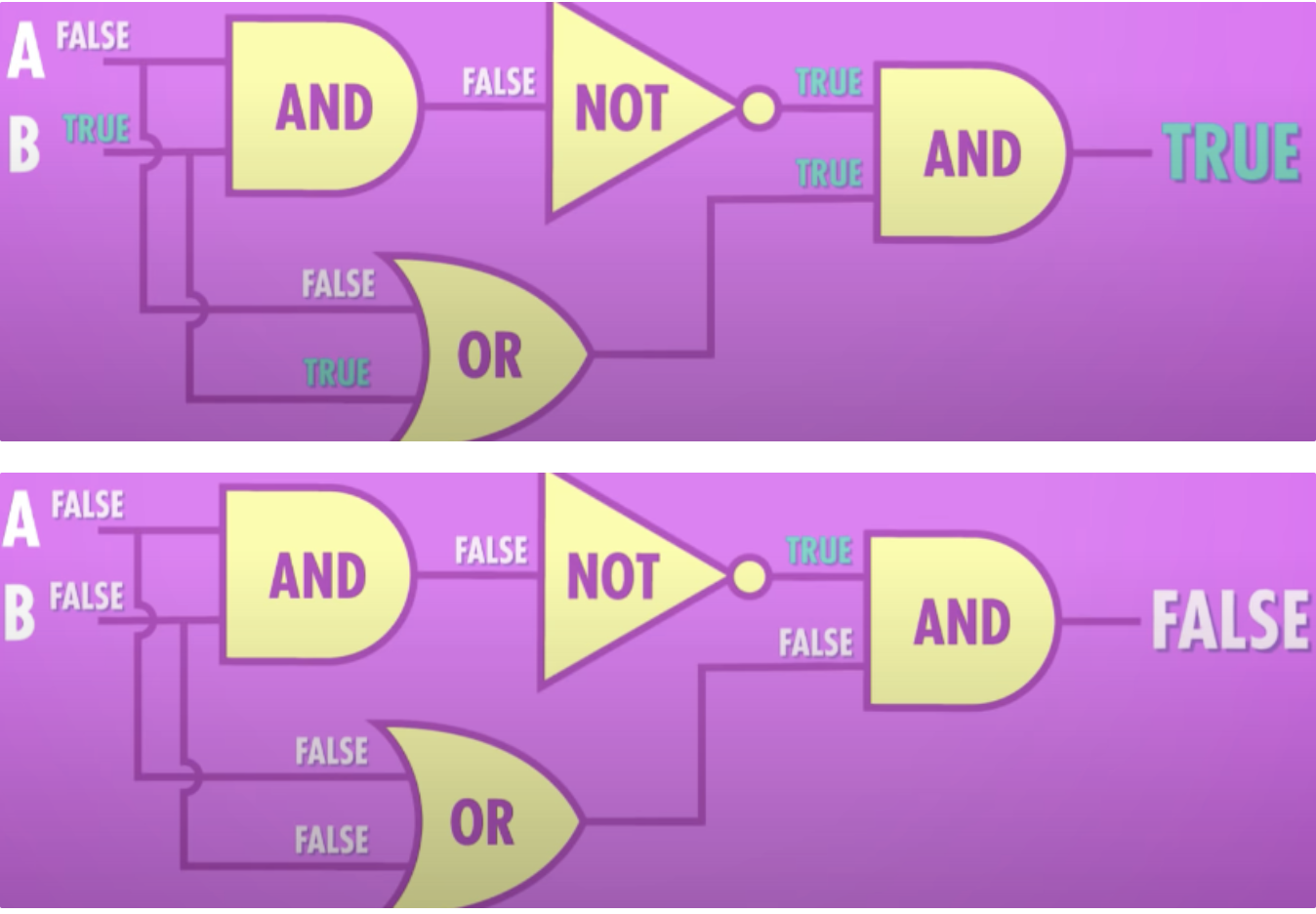
- NOT
- AND
- OR
이 세가지가 부울 대수학의 핵심 연산이다.
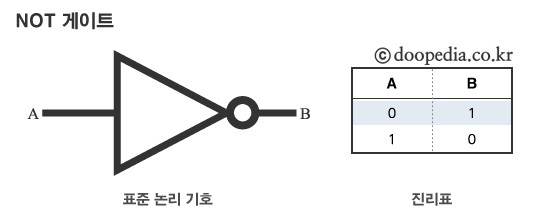
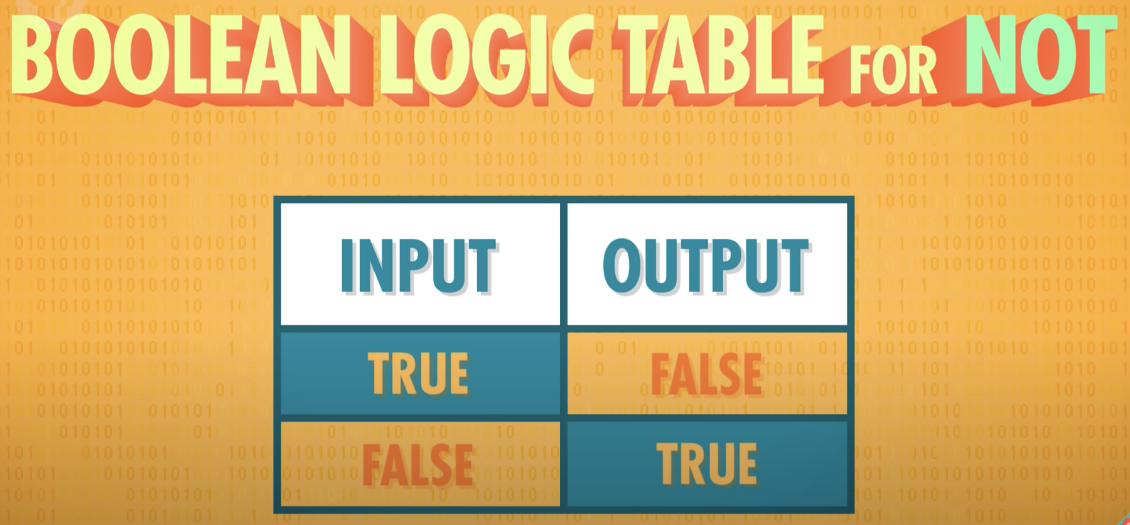
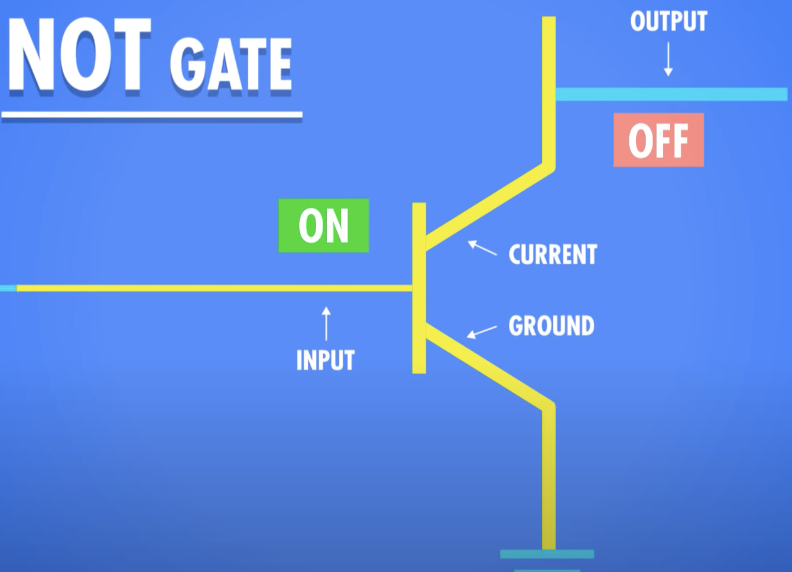
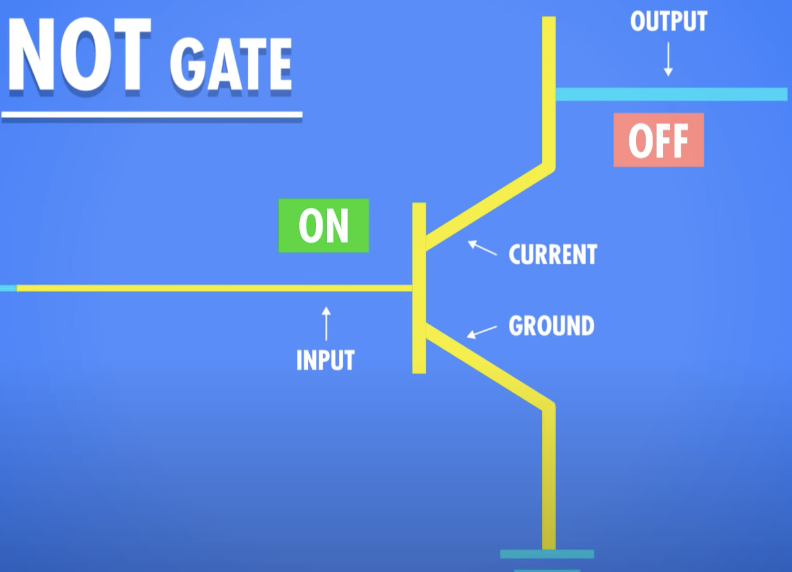
NOT Gate
참이든 거짓이든 그것 중 하나의 값을 취하고 그것을 부정한다
참은 거짓으로, 거짓은 참으로 뒤집는다
- 하나의 입력을 가지며 입력의 반대를 출력하는 논리 Gate
- 논리식은
B = A!이다.
- 코드 구현(swift)
import Foundation
// NOT 게이트
func notGate(param : Bool)->Bool{
let answer : Bool
answer = !param
return answer
}
var a : Bool = True
print("NOT 게이트에 \(a)가 통과하면 \(notGate(param: a))가 됩니다!")
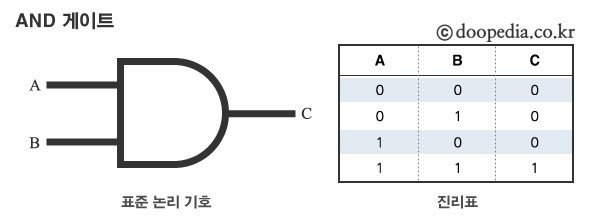
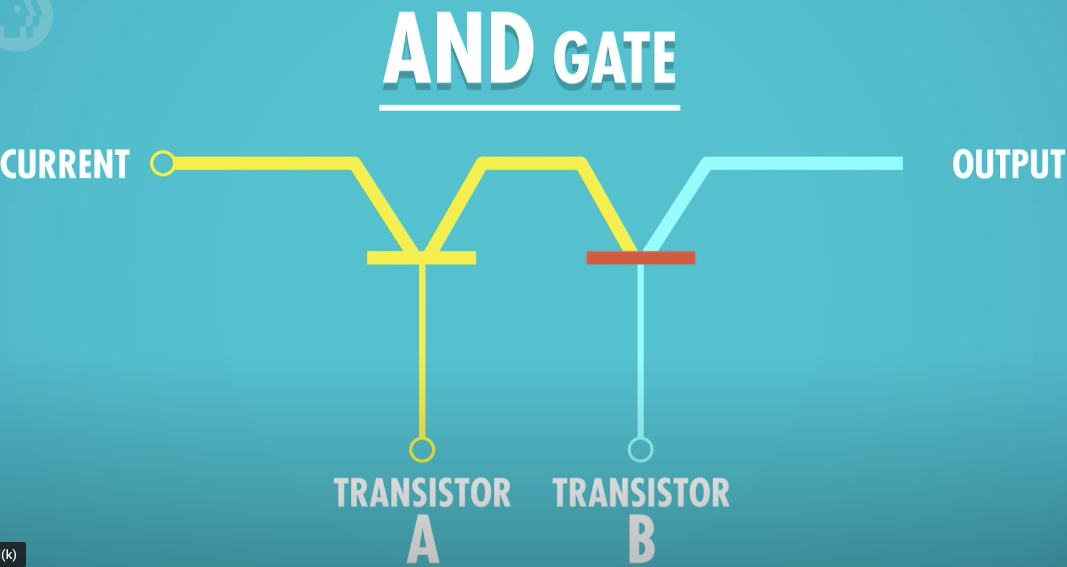
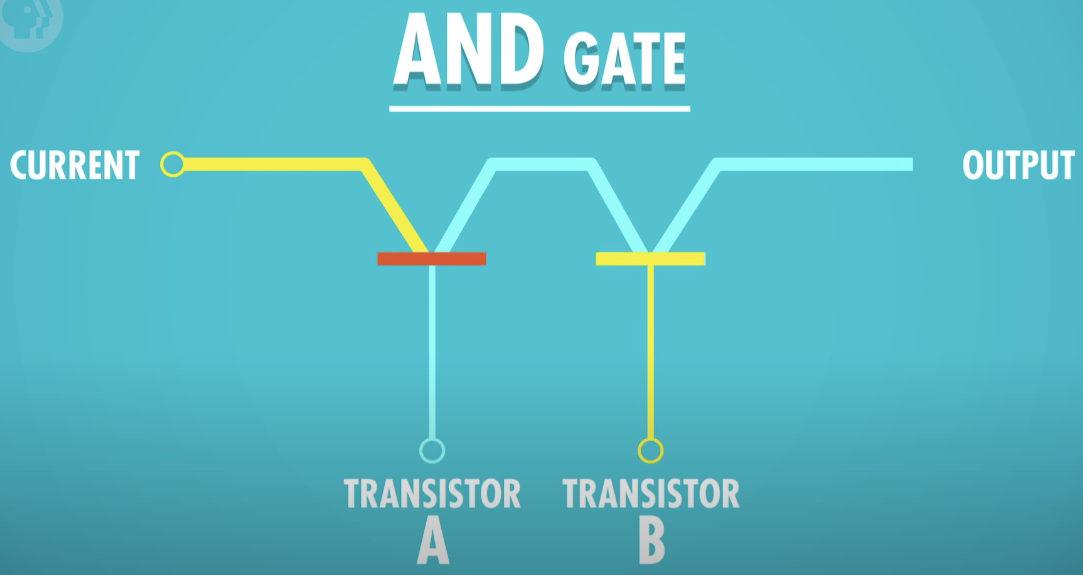
AND Gate
두개의 입력이 필요하지만 여전히 한개의 출력을 한다
이 경우 출력은 모든 입력이 참일 경우만 참이다
- 두개의 입력이 둘다 True일때 True를 반환하는 논리 Gate
- 논리곱을 구현한 것으로 논리식은
C = A * B이다.
- 코드 구현(swift)
import Foundation
// AND 게이트
func andGate(paramA : Bool, paramB: Bool)->Bool{
let answer : Bool
answer = paramA && paramB
return answer
}
var a : Bool = True
var b : Bool = True
print("AND 게이트에 \(a)와 \(b)가 통과하면 \(andGate(paramA: a, paramB: b))가 됩니다!")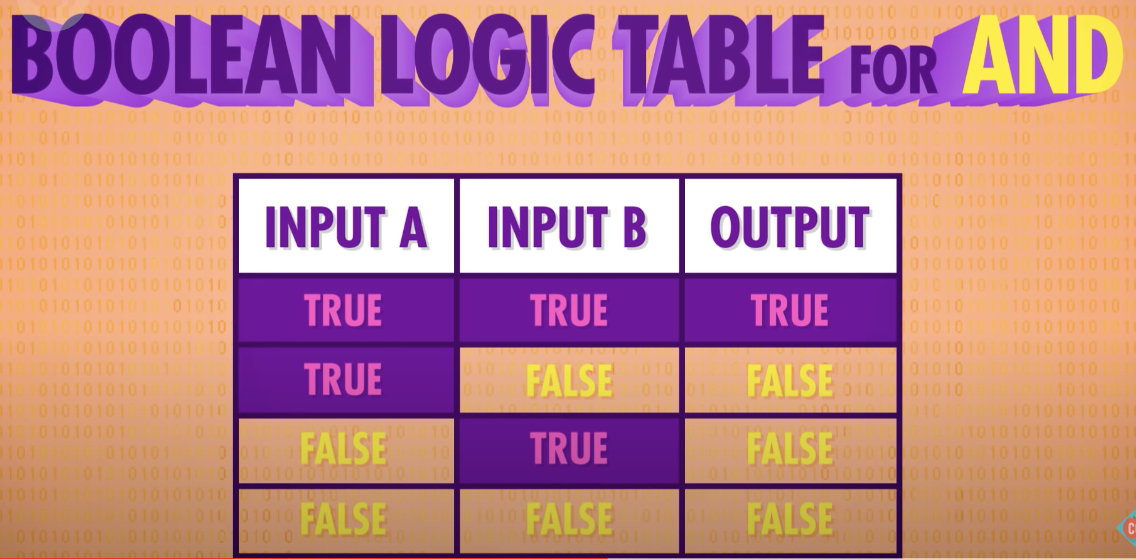
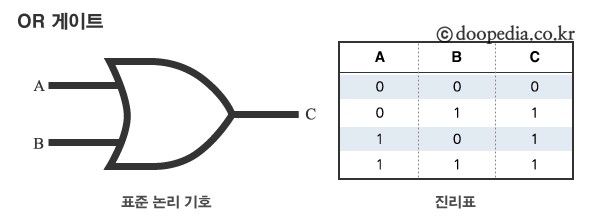
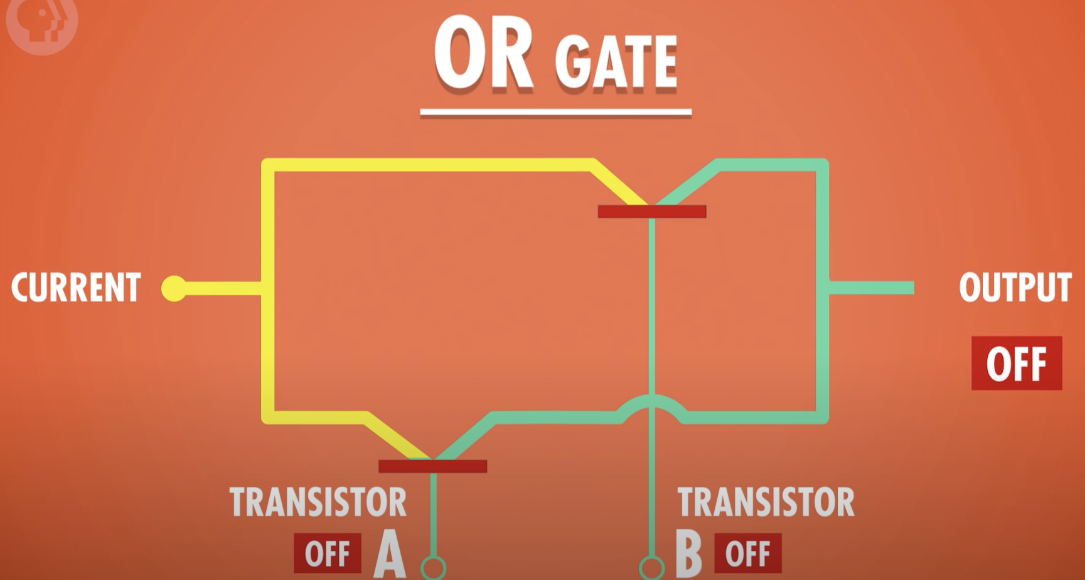
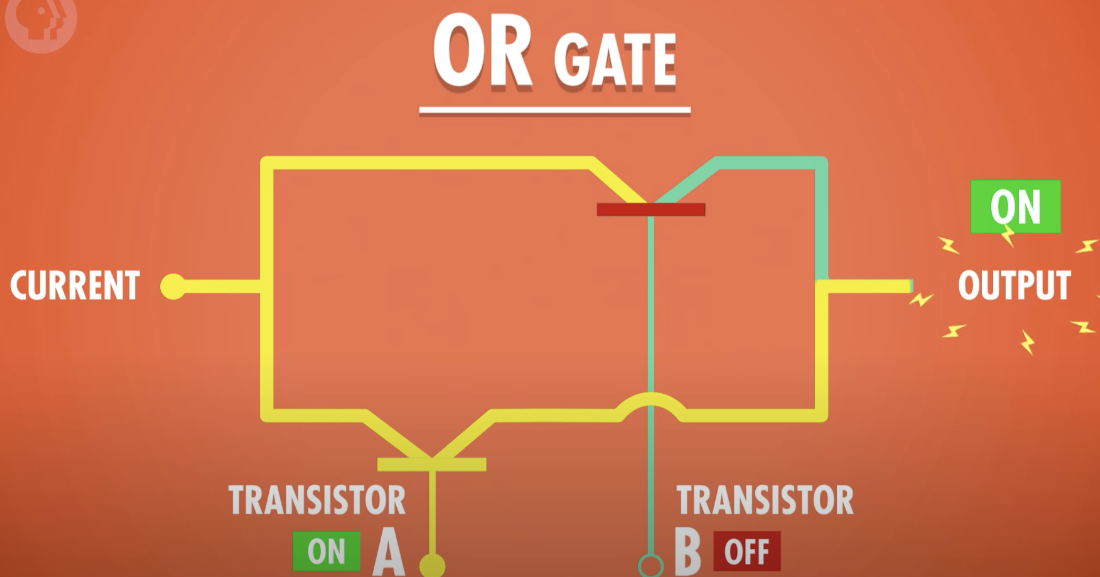
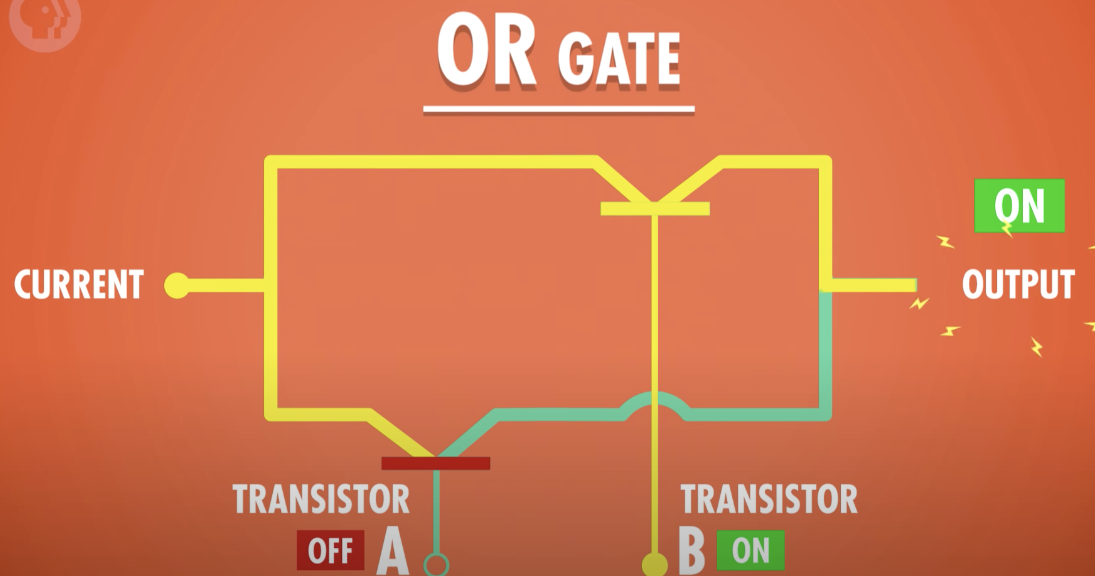
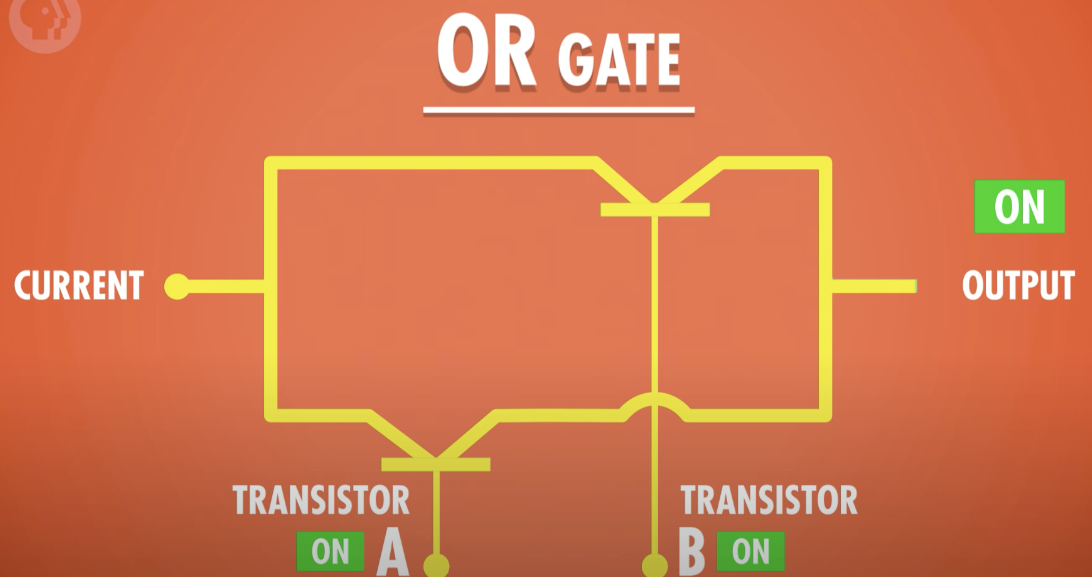
OR Gate
하나의 입력만 참이어도 출력이 참이 되는 연산
- 두개의 입력 중 하나 이상이 True일때 True를 반환하는 논리 Gate
- 논리합을 구현한 것으로 논리식은
C = A + B이다.
- 코드 구현(swift)
import Foundation
// OR 게이트
func orGate(paramA : Bool, paramB: Bool)->Bool{
let answer : Bool
answer = paramA || paramB
return answer
}
var a : Bool = false
var b : Bool = false
print("OR 게이트에 \(a)와 \(b)가 통과하면 \(orGate(paramA: a, paramB: b))가 됩니다!")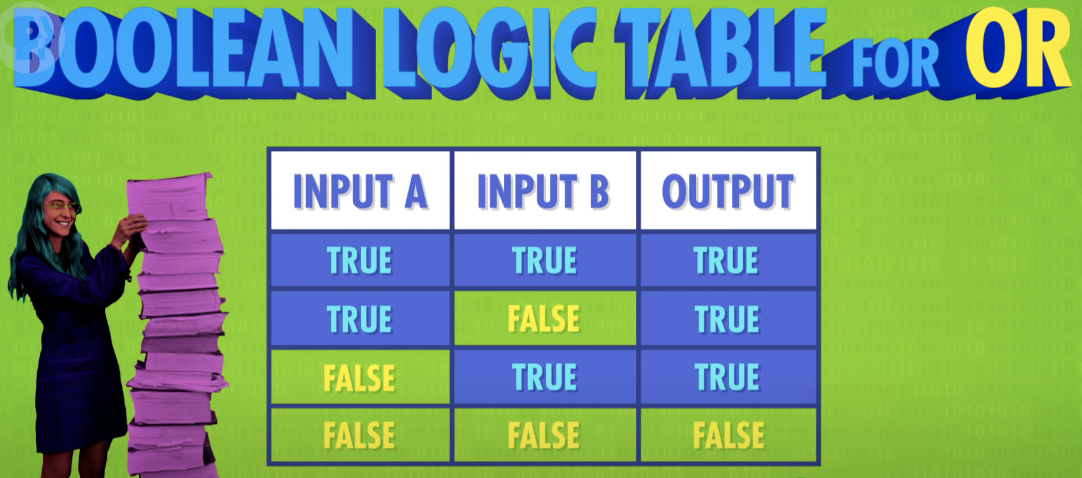
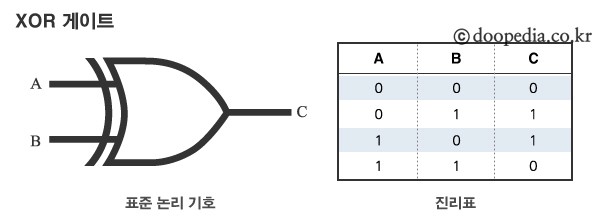
XOR Gate
보통 OR연산과 같지만 하나의 차이점 있다
모든 입력이 참이면, XOR의 출력은 거짓이다
하나의 입력이 참이고 하나는 거짓이면 출력은 참이다
- 두개의 입력이 서로 다른 경우 True를 반환하는 논리 Gate
- 배타적 논리합을 구현한 것으로, 논리식은
C = A * B! + B! * A이다.
- 코드 구현(swift)
import UIKit
// XOR 게이트
func xorGate(paramA : Bool, paramB: Bool)->Bool{
let answer : Bool
answer = (paramA && !paramB) || (!paramA && paramB)
return answer
}
var a : Bool = true
var b : Bool = true
print("XOR 게이트에 \(a)와 \(b)가 통과하면 \(xorGate(paramA: a, paramB: b))가 됩니다!")