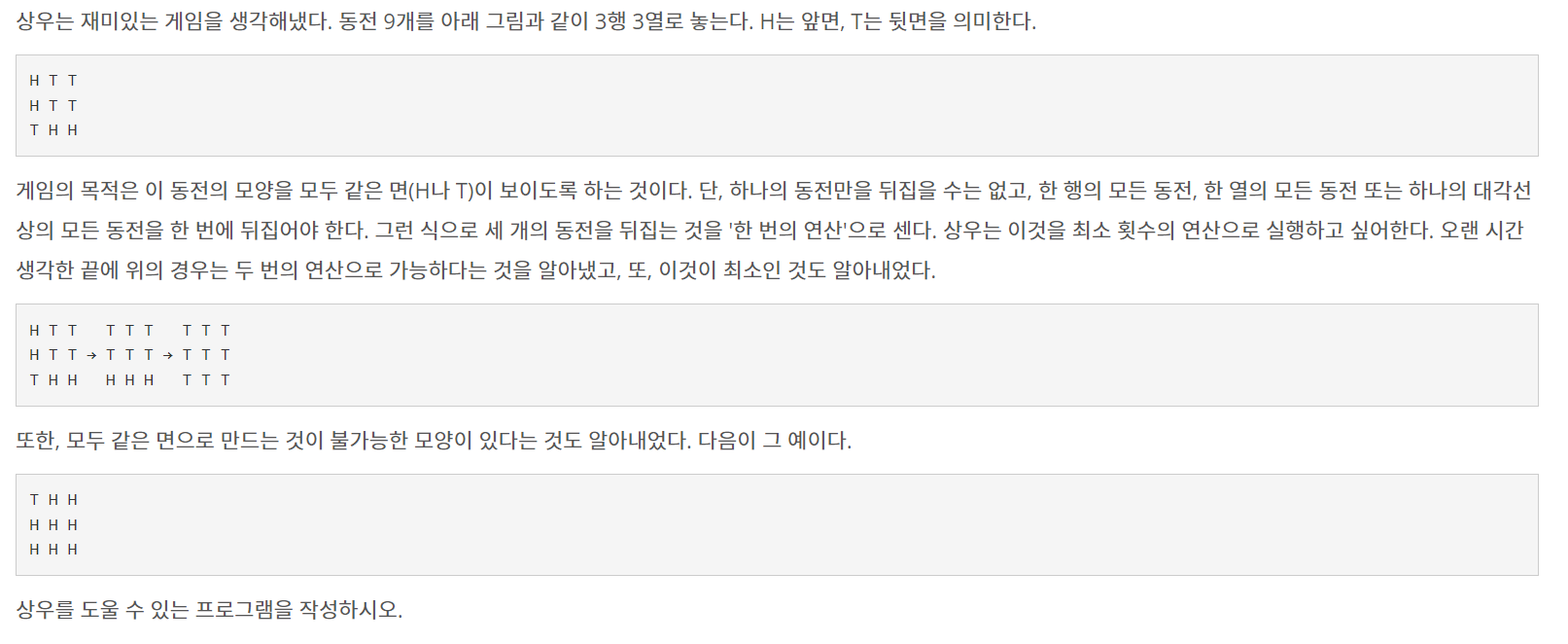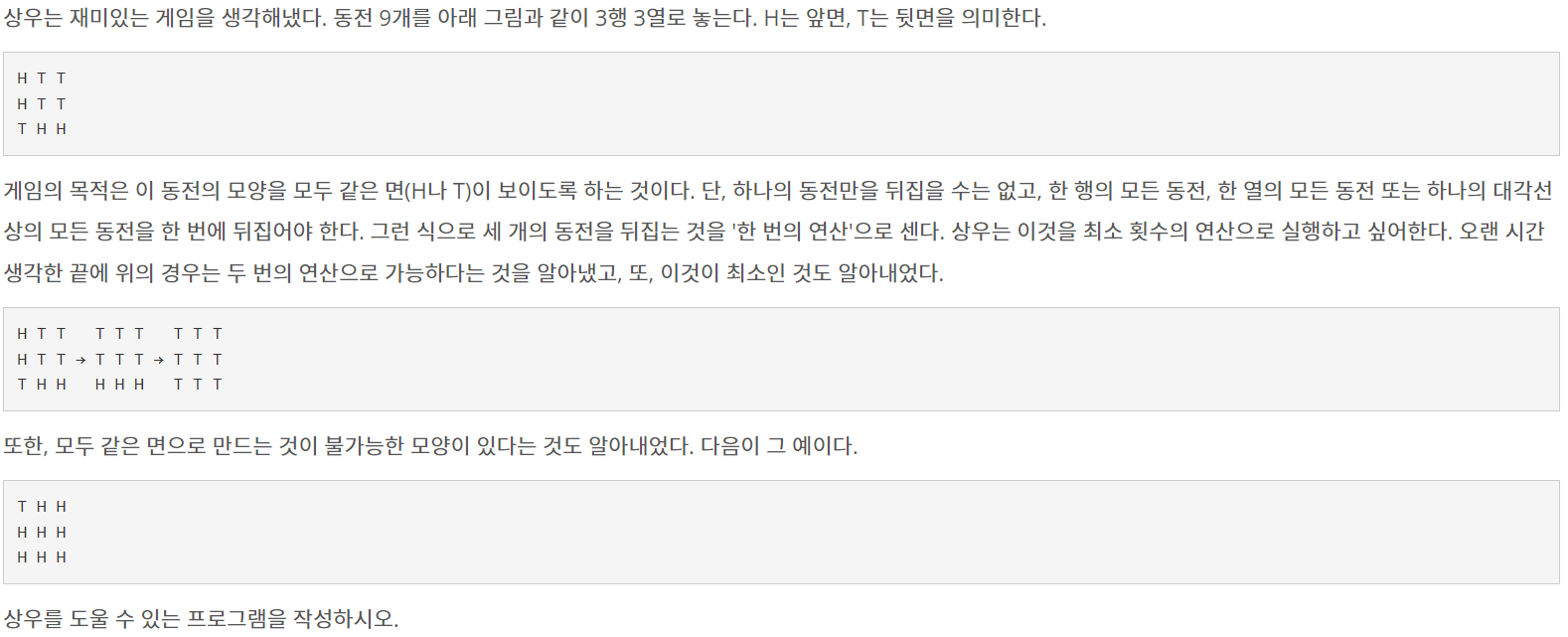
BruteForce13동전게임(9079)
문제
입력
입력의 첫 줄에는 테스트 케이스의 개수 T(1 ≤ T ≤ 10)가 주어진다. 각 테스트 케이스는 세 줄로 이루어지며, 한 줄에 세 개의 동전모양이 주어지는데, 각각의 동전 표시 사이에는 하나의 공백이 주어진다.
출력
각 테스트 케이스에 대해서, 모두 같은 면이 보이도록 만들기 위한 최소 연산 횟수를 출력하고, 불가능한 경우에는 -1을 출력한다.
풀이
코드
import sys
sys.stdin = open("input.txt", "rt")
input = sys.stdin.readline
def find_arr(arr):
global result
for bit_mask in range(2**8):
copy_arr = [row[:] for row in arr]
change_bit = str(bin(bit_mask))[2:].count('1')
if result < change_bit:
continue
for row in range(3):
if bit_mask & (1<<row):
for col in range(3):
copy_arr[row][col] = (copy_arr[row][col]+1)%2
for col in range(3):
if bit_mask & (1<<(col+3)):
for row in range(3):
copy_arr[row][col] = (copy_arr[row][col]+1)%2
if bit_mask & (1<<6):
for row in range(3):
copy_arr[row][row] = (copy_arr[row][row]+1)%2
if bit_mask & (1<<7):
for row in range(3):
copy_arr[row][2-row] = (copy_arr[row][2-row]+1)%2
sum_temp = sum(list(map(sum,copy_arr)))
if sum_temp == 9 or sum_temp == 0:
result = change_bit
T = int(input())
for tc in range(T):
arr = []
result = float('inf') #inf 란 양의 무한대 이다. 즉, 가장 큰 수
for _ in range(3):
s = list(input().split())
for i in range(3):
if s[i] == 'T':
s[i] = 1
else:
s[i] = 0
arr.append(s)
cnt = 0
find_arr(arr)
print(-1 if result == float('inf') else result)배운 것
C++ 방식
// Authored by : tony9402
// Co-authored by : -
// Link : http://boj.kr/98c4781dcf14402db3f83717f0154d5e
#include<bits/stdc++.h>
using namespace std;
int makeBit(string s) {
int bit = 0;
for(int i = 8; i >= 0; i--) {
bit <<= 1;
if(s[i] == 'H') bit |= 1;
}
return bit;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
int T; cin >> T;
while(T--) {
string coin;
bool used[512] = { false };
int answer = -1;
for(int i = 0; i < 9; i++) {
char ch; cin >> ch;
coin += ch;
}
int bit = makeBit(coin);
queue<int> Q;
Q.push(bit);
used[bit] = true;
bool flag = true;
while(!Q.empty() && flag) {
int qsize = Q.size();
answer ++;
while(qsize--) {
int cur = Q.front(); Q.pop();
if(cur == 0 || cur == (1 << 9) - 1) {
flag = false;
break;
}
// 자세한 내용은 맨 아래 Note 참고
for(int nxt : { 7, 56, 448, 73, 146, 292, 273, 84 }) {
int nxtState = cur ^ nxt;
if(used[nxtState]) continue;
used[nxtState] = true;
Q.push(nxtState);
}
}
}
if(flag) answer = -1;
cout << answer << '\n';
}
return 0;
}
/*
* NOTE !!
*
* - 동전 상태를 비트로 저장
* 비트의 위치를 의미
*
* 012
* 345 -> [876543210]
* 678
*
* ex)
* HTT 100
* HTT -> 100 -> 110001001 -> 393
* THH 011
*
*
* - 동전을 뒤집는 경우 값
*
* 111
* 000 -> 000000111 -> 7
* 000
*
* 000
* 111 -> 000111000 -> 56
* 000
*
* 000
* 000 -> 111000000 -> 448
* 111
*
* 100
* 100 -> 001001001 -> 73
* 100
*
* 010
* 010 -> 010010010 -> 146
* 010
*
* 001
* 001 -> 100100100 -> 292
* 001
*
* 100
* 010 -> 100010001 -> 273
* 001
*
* 001
* 010 -> 001010100 -> 84
* 100
*
* - 위 값을 이용하여 동전 뒤집기
*
* HTT THH <--- 요 라인
* HTT -> HTT : 가장 윗 부분 뒤집기
* THH THH
*
* 이를 숫자를 이용하여 계산을 해본다면 아래와 같음
*
* 왼쪽 동전 상태의 값 : 110001001 -> 393
* 가장 위를 뒤집는 값 : 000000111 -> 7
* 오른쪽 동전 상태의 값 : 110001110 -> 398
*
* 해당 위치를 뒤집을 땐 XOR 연산을 이용하면 됨.
*
* 393 ^ 7 => 398
*/