
선수지식으로 트리, 그래프를 배웠다.
트리
: 노드로 이루어진 자료 구조
- 트리의 특징: 순회는 Pre-order, In-order 아니면 Post-order로 이루어진다. 이 3가지 모두 DFS/BFS 안에 있다.
그래프
: 단순히 노드(N, node)와 그 노드를 연결하는 간선(E, edge)을 하나로 모아 놓은 자료 구조
- 그래프의 특징: 순회는 DFS 나 BFS로 가능하다
트리와 그래프의 차이
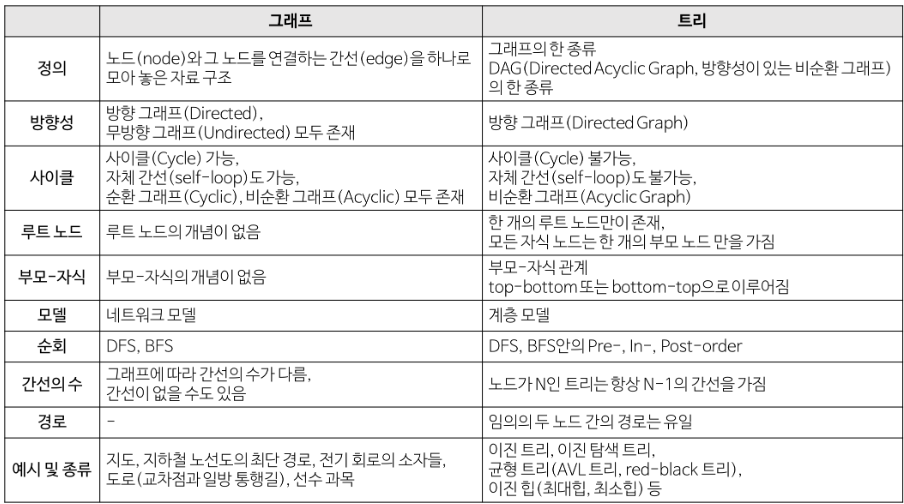
참고.. 이진트리, 트리순회는 또 다른 chapter가 있으니 거기서 깊게 다루자!
DFS(Depth-First Search), 깊이 우선 탐색
깊이 우선 탐색이란?
루트 노드(혹은 다른 임의의 노드)에서 시작해서 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법.
- 미로를 탐색할 때 한 방향으로 갈 수 있을 때까지 계속 가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와서 이곳으로부터 다른 방향으로 다시 탐색을 진행하는 방법과 유사하다.
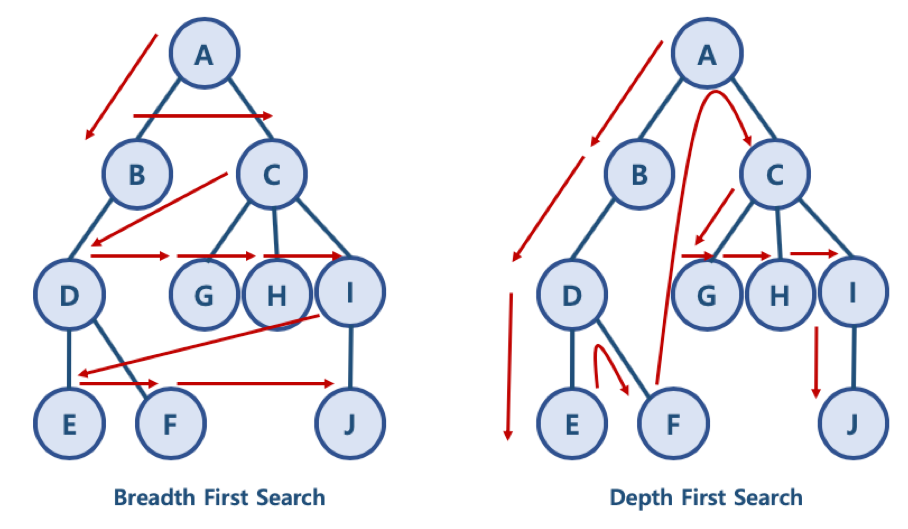
즉, 넓게(wide) 탐색하기 전에 깊게(deep) 탐색하는 것이다.
- 사용하는 경우: 모든 노드를 방문 하고자 하는 경우에 이 방법을 선택한다.
- 깊이 우선 탐색(DFS)이 너비 우선 탐색(BFS)보다 좀 더 간단하다.
- 단순 검색 속도 자체는 너비 우선 탐색(BFS)에 비해서 느리다.
특징
- 넓이 우선 탐색(BFS): BFS는 Queue를 이용하여 구현한다.
- 깊이 우선 탐색(DFS): DFS는 Stack을 이용하여 구현한다.
- DFS 는 자기 자신을 호출하는 순환 알고리즘의 형태를 가지고 있다.
- 전위 순회(Pre-Order Traversals)를 포함한 다른 형태의 트리 순회는 모두 DFS의 한 종류이다. <- 트리순회 chapter에서 다뤄야 할 듯
- 이 알고리즘을 구현할 때 가장 큰 차이점은, 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사해야 한다는 것이다. -> 이를 검사하지 않을 경우 무한루프에 빠질 위험이 있다.

깊이 우선 탐색(DFS)과정
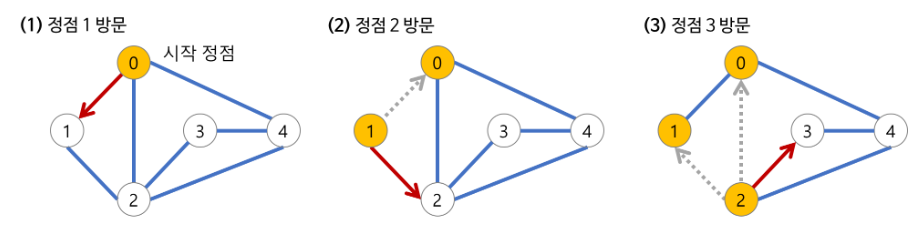
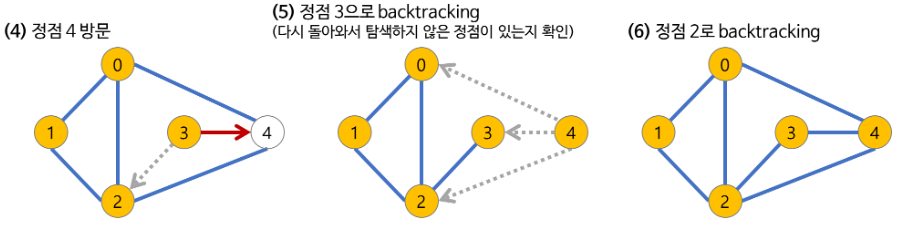
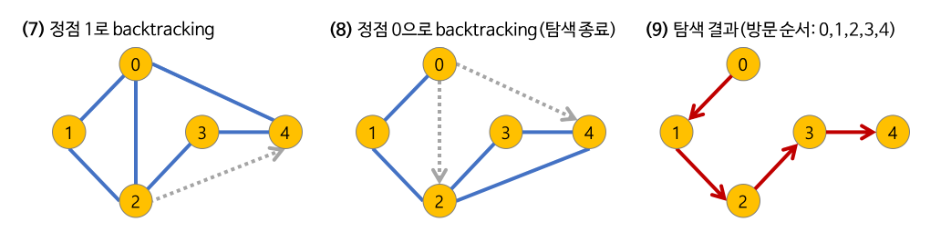
DFS 구현방법 2가지
- 명시적인 Stack 이용
- 순환 호출 이용(Recursion,재귀)
1. Stack을 이용한 DFS
Stack에 시작할 노드를 하나 넣고, 해당 노드의 Child 노드를 다 넣은 후 자식이 없다면, stack에서 꺼낸다 이때 자식 노드가 있다면 Stack에 추가하고, 없다면 출력(Print)한다.
한번 넣었던 노드는 다시 넣지 않는다.

스택이 다 비었다면 순회가 완료된 것이다.
참고 영상
20초 ~ 3:10초
https://www.youtube.com/watch?v=_hxFgg7TLZQ
DFS-Stack 코드(JS)

const graph = {
A: ["B", "C"],
B: ["A", "D"],
C: ["A", "G", "H", "I"],
D: ["B", "E", "F"],
E: ["D"],
F: ["D"],
G: ["C"],
H: ["C"],
I: ["C", "J"],
J: ["I"]
};
const DFS = (graph, startNode) => {
const visited = []; // 탐색을 마친 노드들
let needVisit = []; // 탐색해야할 노드들
needVisit.push(startNode); // 노드 탐색 시작
while (needVisit.length !== 0) { // 탐색해야할 노드가 남아있다면
const node = needVisit.shift(); // queue이기 때문에 선입선출, shift()를 사용한다.
if (!visited.includes(node)) { // 해당 노드가 탐색된 적 없다면
visited.push(node);
needVisit = [...graph[node], ...needVisit];
}
}
return visited;
};
console.log(DFS(graph, "A"));
// ["A", "B", "D", "E", "F", "C", "G", "H", "I", "J"]DFS-Stack 코드(Py)
def dfs(v, graph):
stack = [v]
visited = set()
while stack:
a = stack.pop()
if a in visited: continue
print(a, end = " ")
visited.add(a)
if graph.get(a):
stack.extend(sorted(graph[a], reverse=True))2. 재귀호출을 이용한 DFS:Recursion
재귀를 이용하면 코드가 더욱 간결하고 깔끔해진다.
참고 영상 및 블로그
5:25 ~ 7:53
https://www.youtube.com/watch?v=_hxFgg7TLZQ
+) 이진트리 순회, 조합 참고 - DFS 총정리
https://velog.io/@padd60/JS-%EC%BD%94%ED%85%8C-%EC%9E%AC%EA%B7%80%ED%95%A8%EC%88%98-%EB%B0%8F-DFS-%EC%A0%95%EB%A6%AC-%EA%B7%B8%EB%A6%AC%EA%B3%A0-%EC%9D%91%EC%9A%A9
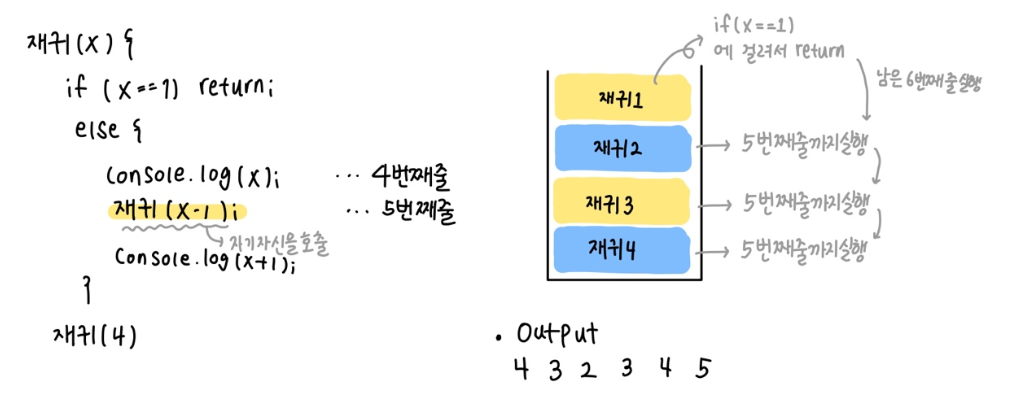
DFS-Recursion 코드(JS)
function DFS(x){
if(x===1) return;
else{
console.log(x);
DFS(x-1);
console.log(x+1);
}
}
DFS(4);스택에 담는다고 생각하면 편하다.
함수를 선언할 때 스택이 만들어 지는데, 스택 안에는 지역변수, 매개변수, 복귀 주소가 들어있다.
DFS-Recursion 코드(Py)
# 재귀함수 사용 1
def dfs(v, graph, visited):
if v in visited: return
print(v, end = " ")
visited.add(v)
# 자식 노드가 있을 때
if graph.get(v):
for c in graph[v]:
dfs(c, graph, visited)시간 복잡도
DFS는 그래프(정점의 수: N, 간선의 수: E)의 모든 간선을 조회한다.
인접 리스트로 표현된 그래프: O(N+E)
인접 행렬로 표현된 그래프: O(N^2)
예시 문제
문제
https://school.programmers.co.kr/learn/courses/30/lessons/43162
풀이
https://velog.io/@timointhebush/%ED%94%84%EB%A1%9C%EA%B7%B8%EB%9E%98%EB%A8%B8%EC%8A%A4-%EB%84%A4%ED%8A%B8%EC%9B%8C%ED%81%AC-DFS-BFS-Python
코드
def solution(n, computers):
answer = 0
visited = [False for i in range(n)]
for com in range(n):
if visited[com] == False:
DFS(n, computers, com, visited)
answer += 1 #DFS로 최대한 컴퓨터들을 방문하고 빠져나오게 되면 그것이 하나의 네트워크.
return answer
def DFS(n, computers, com, visited):
visited[com] = True
for connect in range(n):
if connect != com and computers[com][connect] == 1: #연결된 컴퓨터
if visited[connect] == False: