Part7.12_동적프로그래밍(DynamicProgramming)_플로이드 워샬 알고리즘

문제

입력

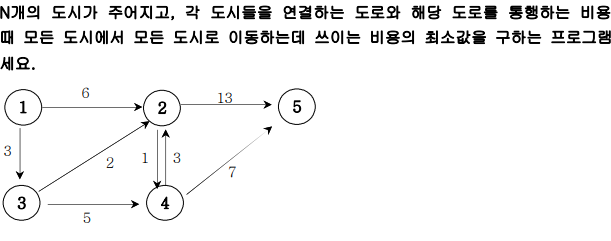
첫 번째 줄에는 도시의 수N(N<=100)과 도로수 M(M<=200)가 주어지고, M줄에 걸쳐 도로정보
와 비용(20 이하의 자연수)이 주어진다. 만약 1번 도시와 2번도시가 연결되고 그 비용이 13이
면 “1 2 13”으로 주어진다.

출력

모든 도시에서 모든 도시로 이동하는데 드는 최소 비용을 아래와 같이 출력한다.
자기자신으로 가는 비용은 0입니다. i번 정점에서 j번 정점으로 갈 수 없을 때는 비용을 “M"으
로 출력합니다.

정답 풀이

• 플로이드 워샬 알고리즘

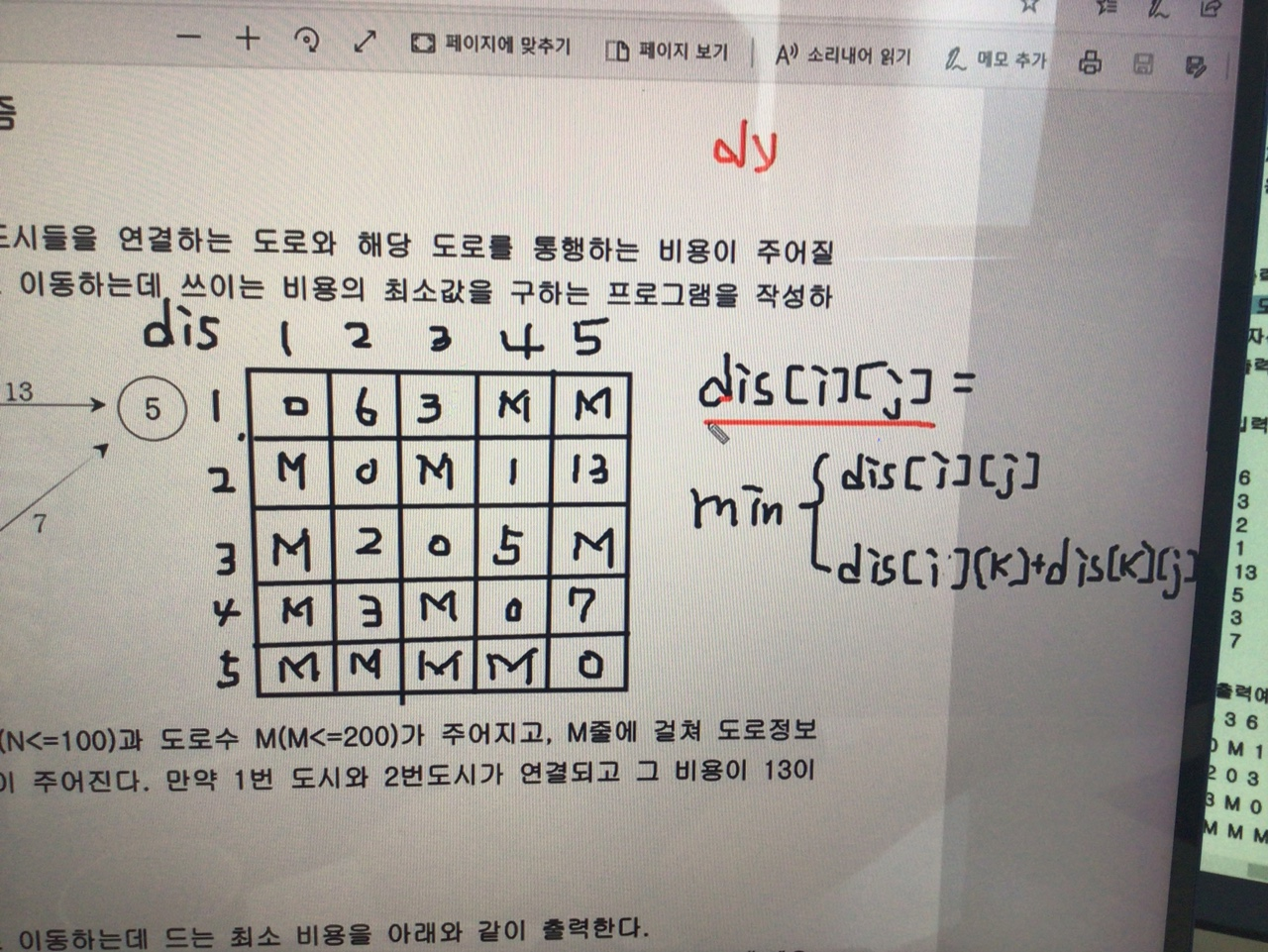
0. 이차원 배열의 모든 값을 5000으로 초기화 한다,
1. 가장 먼저 경유 없이 직행으로 갈 수 있도록 갱신한다.
   
   2.3중 for문 구현
   

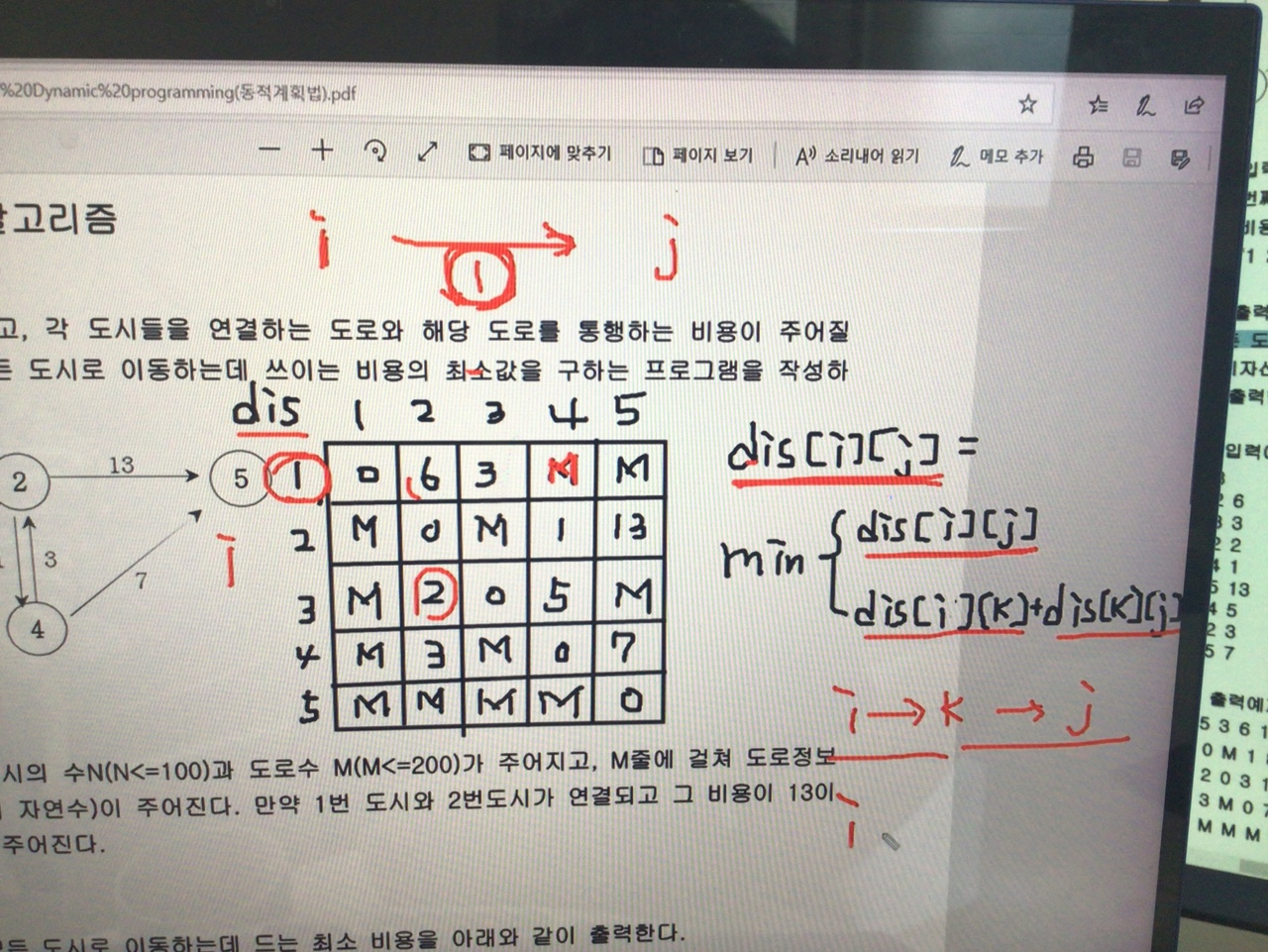
가장 상위(3중for문) for문의 k값이 바뀔 때 마다 이중 for문을 돌면서 배열을 갱신한다.
i -> k -> j 일 때(k를 경유할 때) 가장 최솟값으로

정답 코드

import sys
sys.stdin = open ("input.txt", "rt")

def input():
    return sys.stdin.readline().rstrip()

if __name__ == "__main__":
    #n 은 정점번호, m은 간선의 개수
    n, m = map(int,input().split())
    # 냅색 알고리즘과 동일한 원리이다.
    #경유지를 1부터 N까지 경유해서 가는 방법을 갱신한다
    dis=[[5000]*(n+1) for _ in range(n+1)]

    for i in range(1,n+1):
        dis[i][i] = 0 #대각선 0으로 초기화

    for i in range(m):#최초로 인접행렬로 초기화(아무 노드 거치지 않고 직행)
        a,b,c = map(int,input().split())
        dis[a][b] = c

    for k in range(1, n+1):# 프로이드 워샬 알고리즘
        # k기 바뀔때마다 아래 이차원리스트 갱신.
        for i in range(1,n+1):
            for j in range(1,n+1):
                dis[i][j] = min(dis[i][j], dis[i][k]+dis[k][j])
                # 다이나믹 테이블 값 갱신 i -> k -> j 를 거쳐서 간 최소값
                
        for i in range(1,n+1):
            for j in range(1,n+1):
                if dis[i][j] == 5000:
                    print("M", end=' ')
                else:
                    print(dis[i][j], end=" ")

코멘트

플로이드 워샬 알고리즘 딱딱 나올 수 있도록 공부 더 해놓자