멱집합

집합 {1, 2, 3}의 모든 부분집합은 {}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3} 으로 나열할 수 있고, 이 부분집합의 총 개수는 8개이다. 그리고 이 모든 부분집합을 통틀어 멱집합이라고 한다.

이렇게 어떤 집합이 있을 때, 이 집합의 모든 부분집합을 멱집합 이라고 한다. 모든 부분집합을 나열하는 방법은 다음과 같이 몇 단계로 구분할 수 있다. 부분집합을 나열하는 방법에서 가장 앞 원소(혹은 임의의 집합 원소)가 있는지, 없는지에 따라 단계를 나누는 기준을 결정한다.

Step A: 1을 제외한 {2, 3}의 부분집합을 나열

• Step B: 2를 제외한 {3}의 부분집합을 나열합
  - Step C: 3을 제외한 {}의 부분집합을 나열 → {}
  - Step C: {}의 모든 부분집합에 {3}을 추가한 집합들을 나열 → {3}
• Step B: {3}의 모든 부분집합에 {2}를 추가한 집합들을 나열
  - Step C: {3}의 모든 부분집합에 {2}를 추가한 집합들을 나열 하려면, {}의 모든 부분집합에 {2}를 추가한 집합들을 나열한 다음 {}의 모든 부분집합에 {2, 3}을 추가한 집합들을 나열 → {2}, {2, 3}

Step A: {2, 3}의 모든 부분집합에 {1}을 추가한 집합들을 나열

• Step B: {2, 3}의 모든 부분집합에 {1}을 추가한 집합들을 나열하려면, {3}의 모든 부분집합에 {1}을 추가한 집합들을 나열한 다음 {3}의 모든 부분집합에 {1, 2}를 추가한 집합들을 나열
  - Step C: {3}의 모든 부분집합에 {1}을 추가한 집합을 나열하려면, {}의 모든 부분집합에 {1}을 추가한 집합들을 나열한 다음 {}의 모든 부분집합에 {1, 3}을 추가한 집합들을 나열 → {1}, {1, 3}
  - Step C: {3}의 모든 부분집합에 {1, 2}를 추가한 집합을 나열하려면, {}의 모든 부분집합에 {1, 2}를 추가한 집합들을 나열한 다음 {}의 모든 부분집합에 {1, 2, 3}을 추가한 집합들을 나열 → {1, 2}, {1, 2, 3}

원소가 있는지, 없는지 2가지 경우를 고려하기 때문에 집합의 요소가 n 개일 때 모든 부분집합의 개수는 2^n개 이다. 예를 들어 집합의 원소가 4개라면 모든 부분집합의 개수는 24, 집합의 원소가 5개라면 25가 된다.

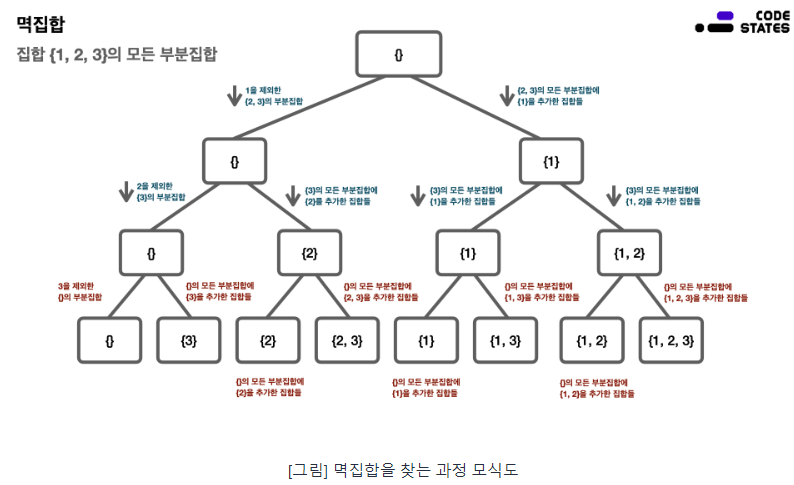
멱집합을 구하는 방법에서 각 단계를 유심히 살펴보면, 순환 구조를 띠는 것을 확인할 수 있다. 여기서 순환구조는 임의의 원소를 제외하면서 집합을 작은 단위로 줄여나가는 방법입니다. 따라서, 문제를 작은 단위로 줄여나가는 재귀를 응용할 수 있다.

멱집합 - Power Set

집합 S가 있을 때, Power Set인 P(S)는 집합 S의 거듭제곱 집합으로, S의 모든 부분 집합의 집합을 의미한다.

예를 들어 S가 {a, b, c} 으로 요소가 3개일 때,

P(S)는 {{}, {a}, {b}, {c}, {a,b}, {a, c}, {b, c}, {a, b, c}} 으로 요소가 8개임을 알 수 있다.

즉 S에 n개의 요소가 있다면 P(S)에는 2^n의 요소가 있음을 의미한다.

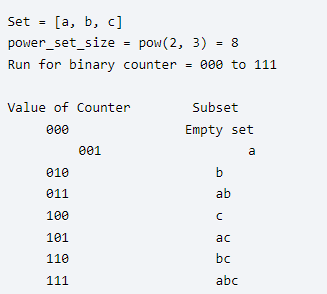
이제 알고리즘 로직을 보도록 하겠다.

모든 집합의 크기를 가져온다.
power_set_size = pow(2, set_size)
0에서부터 power_set_size까지의 반복문 실행

i = 0에서 set_size까지 크기를 지정해 반복문을 돌린다. 그리고 집합에서 i번째 요소에 해당하는 하위 집합을 출력한다.
하위 집합을 구하면 개행을 통해 집합을 구분한다.

주어진 집합 S에 대해 거듭제곱 집합은 0과 2^n-1 사이의 모든 이진수를 생성하여 찾을 수 있다. 여기서 n은 집합의 크기이다. 예를 들어 집합 S {x, y, z}에 대해 0부터 2^3-1까지의 모든 이진수를 생성하고, 생성된 각 숫자에대해 해당 숫자의 집합 비트를 고려하여 해당 집합을 찾을 수 있다.

let inputSet = ['a', 'b', 'c'];

function powerSet (arr) {
	const result = [];

	function recursion (subset, start) {
		result.push(subset);

		for(let i = start; i < arr.length; i++){
			recursion([...subset, arr[i]], i+1);
			//이렇게도 구현할 수 있습니다.
			recursion(subset.concat(arr[i]), i+1);
		}
	}

	recursion([], 0);

	return result;
}

poserSet(inputSet);

// OUTPUT
//[
//  [],
//  [ 'a' ],
//  [ 'a', 'b' ],
//  [ 'a', 'b', 'c' ],
//  [ 'a', 'c' ],
//  [ 'b' ],
//  [ 'b', 'c' ],
//  [ 'c' ]
//]

위의 powerSet 로직은 재귀함수를 이용하여 구현한 것이다. 재귀함수에 부분집합을 만들기 위한 빈배열과 시작할 숫자를 지정한다. 이어 숫자가 커지게끔 하면서 중심 로직인 반복문을 돌려 부분집합을 만든 뒤, 최종적으로 배열 result에 push한다.