[MML] 2. 선형대수학(Linear Algebra)

yourjin·2024년 9월 8일

dev.log

목록 보기

14/14

2.1. 연립일차방정식의 시스템(Systems of Linear Equations)

일반적으로 연립일차방정식의 해는 세 가지 경우 중 한 경우가 된다.
1. 해가 없는 경우
2. 해가 하나 존재하는 경우
3. 무수히 많은 해가 존재하는 경우
연립선형방정식의 계수들을 모아서 한꺼번에 한 벡터로 표현하여 풀 수 있다.

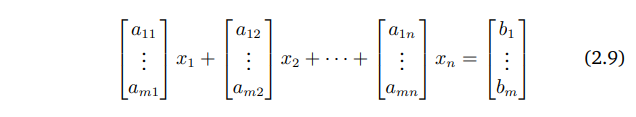
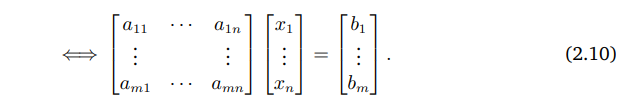
2.2. 행렬(Matrices)

단위행렬(Identity Matrix)

대각선 원소가 모두 1이고 나머지 원소가 모두 0인 정사각행렬이다.
행렬의 곱셈에서 항등원 역할을 한다.
(항등원: 어떤 연산에 대해, 그 연산을 적용했을 때도 원래 값이 변하지 않는 값)

I = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}

역행렬(Inverse Matrix)

행렬 $A$ 의 역행렬 $A^{-1}$ 은 $A$ 와 곱했을 때 단위행렬이 되는 행렬을 말한다.
모든 행렬이 역행렬을 가지는 것은 아니다. 역행렬이 존재하려면 행렬이 정사각행렬이어야 하고, 행렬식(det)이 0이 아니어야 한다.

전치행렬(Transpose Matrix)

행렬 $A$ 의 전치행렬 $A^T$ 은 행과 열을 뒤바꾼 행렬이다.
즉 $A$ 의 (i, j) 원소는 $A^T$ 의 (j, i) 원소가 된다.

A = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix} , A^T = \begin{pmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{pmatrix}

대칭행렬(Symmetric Matrix)

전치행렬과 원래 행렬이 같은 행렬을 말합니다. 즉, 행렬 $A$ 가 $A^T = A$ 를 만족하면 $A$ 는 대칭행렬입니다.
대칭행렬의 원소는 주대각선을 기준으로 대칭입니다.

A = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 4 & 5 \\ 3 & 5 & 6 \end{pmatrix}

행렬의 연칙

결합법칙
- 덧셈의 결합법칙: $A+(B+C)=(A+B)+C$
- 곱셈의 결합법칙: $A(BC)=(AB)C$
분배법칙
- $A(B+C)=AB+AC$
- $(A+B)C=AC+BC$

2.3. 연립일차방정식의 풀이(Solving Systems of Linear Equations)

일반해와 특수해

특수해는 연립일차방정식의 해 중 하나의 값을 의미한다.
일반해는 특수해와 하나로 특정화 되지 않는 일반해의 형식으로 얻을 수 있다.
일반적인 접근법은 다음과 같은 3가지 단계로 구성되어 있다.
1. $Ax=b$ 의 특수해를 찾는다
2. $Ax=0$ 의 모든 해를 찾는다.
3. 위의 두 단계의 모든 해를 종합하여 일반해의 형태로 전환한다.

성분 변환(Elementary transformation)

연립일차방정식을 해결하기 위해 행렬을 간소화 하는 과정에서 사용되는 세 가지 기본적인 연산으로, 이 연산들을 통해 “행 사다리꼴(Row Echelon Form)으로 변환하여 쉽게 해를 구할 수 있다.

두 행을 교환 (Row Swap)
- 행렬에서 두 행의 위치를 서로 바꾼다
- ex) $R_1$ 과 $R_2$ 를 교환하는 연산은 $R_1↔R_2$ 로 표기한다.
한 행에 상수를 곱함 (Scaling a Row)
- 한 행의 모든 성분에 동일한 상수를 곱한다.
- ex) $R_1$ 을 3배하는 연산은 $R_1→3R_1$ 로 표기합니다.
한 행에 다른 행의 배를 더함 (Row Addition/Subtraction)
- 한 행에 다른 행의 배를 더하거나 빼서 변형한다.
- ex) $R_2$ 에 $R_1$ 의 2배를 더하는 연산은 $R_2→R_2+2R_1$ 로 표기합니다.

가우시안 소거법(Gaussian elimination)

가우시안 소거법은 선형 방정식의 해를 구하기 위한 방법이다.

전진 소거 (Forward Elimination)
- 성분 변환을 통해 행렬을 행 사다리꼴로 변환한다.
- 행 사다리꼴은 상삼각 행렬 형태로 아래 삼각형 부분의 모든 성분이 0인 형태를 말한다.
역대입 (Back Substitution)
- 마지막 방정식부터 시작해 차례로 이전 방정식의 값을 구하고, 그 값을 이용해 나머지 변수들을 하나씩 구한다.

ex)

연립일차방정식

x+2y+z=9\\ 2x+3y+3z=21\\ 3x+y+2z=14

전진 소거 후의 행렬

\begin{pmatrix} 1 & 2 & 1 & 9 \\ 0 & -1 & 1 & 3 \\ 0 & 0 & 2 & 2 \end{pmatrix}

역대입을 통한 변수 계산

2z=2 → z=1\\ -y+z=3, y=z-3 → y=-2\\ x+2y+z=9, x=9-2y-z → x=12

행 사다리꼴 행렬 (Row-Echelom Form)

모든 0이 아닌 행은 0으로만 이루어진 행보다 위에 있어야 한다.
- 즉, 모든 0으로 이루어진 행은 행렬의 하단에 위치해야 합니다.
각 행에서 가장 왼쪽에 있는 0이 아닌 수(pivot 또는 leading entry)는 윗줄에 있는 pivot보다 오른쪽에 위치해야 한다.
- 각 행에서 pivot은 그 윗줄에 있는 pivot보다 오른쪽에 있어야 합니다. 즉, pivot이 왼쪽에서 오른쪽으로 "사다리"처럼 내려가는 형태가 됩니다.
pivot 열의 값은 0이 아니며, 그 아래에 있는 값들은 모두 0이어야 한다.
- 각 pivot이 위치한 열에서는 그 아래의 모든 성분이 0이어야 합니다.

ex)

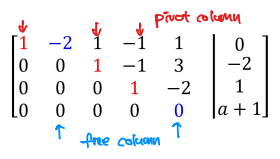
pivot(basic) variable: $x_1, x_3, x_4$
free variable: $x_2, x_5$

기초 변수(Basic Variable)

행 사다리꼴 행렬의 pivot 칼럼(각 행에서 첫 번째로 0이 아닌 항목이 있는 열)에 해당하는 변수들이다.
자유 변수의 값에 종속되어, 자유 변수가 정해지면 그 값이 정해지는 변수를 말한다. → 방정식에서 다른 변수에 의해 값이 결정되는 변수를 말한다.
기초 변수는 선형 시스템의 특정 해를 결정하는 데 사용된다.

자유 변수(Free Variables)

기초 변수가 아닌 나머지 변수들을 말한다.
자유 변수는 값을 자유롭게 선택할 수 있으며, 선택한 값에 따라 기초 변수의 값이 결정된다.
자유 변수는 선형 시스템의 해가 무수히 많은 경우 그 해를 표현하는 데 사용된다. 선형 방정식 시스템에서 독립적인 방정식 수가 변수의 수보다 적을 때 발생한다.

기약 행 사다리꼴(Reduced Row-Echelon)

Reduced Row-Echelon은 직관적인 방법으로 일반해를 결정할 수 있게 하기 때문에 매우 중요한 역할을 한다.

가우시안 소거법은 선형 방정식을 성분 변환을 통해 Reduced Row-Echelon 형태로 바꾸기 위한 하나의 알고리즘이다.

Row-Echelon Form이다.
모든 pivot이 1이다.
피벗은 해당 열의 0이 아닌 유일한 항목이다.

음의 -1 트릭(The minus-1 Trick)

행 연산 중에서 한 행에 상수를 곱하는 연산의 일환으로, 특히 -1을 곱해 값을 뒤집거나 0을 만들기 위해 사용되는 기법이다.

가우시안 소거법을 이용한 역행렬 계산

가우시안 소거법을 통해 행렬을 기약 행 사다리꼴(Reduced Row Echelon Form)으로 변환하면서, 역행렬을 구할 수 있다.

시작 행렬 작성
주어진 행렬 $A$ 와 동일한 크기의 단위행렬 $I$ 을 나란히 놓습니다.
```
$$
\left[ A \mid I \right] = \begin{pmatrix}
a & b & 1 & 0 \\
c & d & 0 & 1
\end{pmatrix}

$$
```
행 연산을 통해 $A$ 를 단위행렬로 변환
가우시안 소거법을 사용하여 A를 단위행렬로 바꾸어줍니다. 이때, 단위행렬이었던 부분이 변형되며 역행렬 $A^{-1}$ 이 됩니다.
결과 확인
최종적으로 $[ I | A^{-1}]$ 의 형태가 완성됩니다. 여기서 오른쪽에 있는 행렬이 역행렬 $A^{-1}$ 이 됩니다.

\left[ I \mid A^{-1} \right] = \begin{pmatrix}1 & 0 & x & y \\0 & 1 & z & w\end{pmatrix}

2.4. 벡터 공간(Vector Spaces)

벡터 공간(Vector space)

벡터 공간은 벡터의 집합으로, 벡터의 덧셈과 스칼라 곱셈이라는 두 가지 연산을 만족해야 합니다.

(여기서 $u$ , $v$ 는 벡터이고, $c$ 는 스칼라입니다.)

덧셈에 대해 닫힘성
벡터 공간 내의 두 벡터를 더한 결과는 다시 벡터 공간 내의 벡터이다.
```
$$
\mathbf{u} + \mathbf{v} \in V
$$
```
스칼라 곱에 대해 닫힘성
스칼라 값과 벡터 공간 내의 벡터를 곱한 결과는 다시 벡터 공간 내의 벡터이다.
```
$$
c\mathbf{v} \in V
$$
```

벡터 부분 공간(Vector Subspace)

벡터 부분 공간은 벡터 공간의 부분 집합으로, 그 자체가 또 하나의 벡터 공간이다. 벡터 부분 공간은 벡터 공간의 성질을 그대로 물려받으며, 벡터 덧셈과 스칼라 곱에 대해 닫혀 있어야 한다.

군(Groups)

집합과 그 집합 위에서 정의된 하나의 이항 연산(두 요소를 결합하여 새로운 요소를 만드는 연산)을 다룬다. 군은 네 가지 기본 성질을 만족하는 구조로 정의된다.

폐쇄성(Closure)
- 집합 내의 두 원소에 대해 연산을 수행했을 때 그 결과가 다시 그 집합 내에 존재해야 한다.
- 예: a∗b∈G (여기서 G는 군, a,b는 G의 원소)
결합법칙(Associativity)
- 세 원소의 연산 순서는 결과에 영향을 미치지 않는다.
- 예: (a∗b)∗c=a∗(b∗c)
항등원(Identity Element)
- 군 내에 어떤 원소 e가 존재하여, 그 원소와 다른 원소를 연산해도 원래의 원소가 유지된다.
- 예: a∗e=a (항등원 e)
역원(Inverse Element)
- 각 원소는 자기 자신과 연산했을 때 항등원을 만들어내는 역원이 존재한다.
- 예: a∗a−1=e (여기서 a−1는 a의 역원)

군의 예로는 정수 집합에서 덧셈 연산을 예로 들 수 있다. 모든 정수는 덧셈에 대해 항등원(0)과 역원(음수)을 가지므로, 이는 군을 이룬다.

일반 선형군(General Linear Group)

정사각 행렬의 군으로, 주어진 차원에서 역행렬이 존재하는 모든 정사각 행렬의 집합을 가리킨다.

GL(n,F)는 차원 n과 체 F(일반적으로 실수 또는 복소수)를 가진 모든 n×n 행렬로 구성되며, 그 행렬들의 곱셈에 대한 군이다.

이 집합 내의 모든 행렬은 역행렬을 가지고, 행렬 곱셈이 군의 연산이다.

2.5. 선형독립성(Linear Independence)

선형 독립성(Linear Independence): 한 집합의 벡터들이 서로 선형 결합으로 표현되지 않으면 선형 독립이다.
선형 종속성(Linear dependence): 한 벡터가 다른 벡터들의 선형 결합으로 표현될 수 있으면 그 벡터들은 선형 종속적이다.

2.6. 기저와 랭크(Basis and Rank)

기저(Basis): 벡터 공간을 생성하는 최소 집합으로, 선형 독립인 벡터들로 구성된다.
랭크(Rank): 행렬의 랭크는 행렬의 기저를 이루는 벡터의 개수로 정의된다.

2.7. 선형 사상(Linear Mappings)

선형 사상: 두 벡터 공간 사이의 선형 변환을 의미하며, 덧셈과 스칼라 곱을 보존하는 함수이다.
- 단사(Injective): 서로 다른 입력이 서로 다른 출력을 낳는 사상.
- 전사(Surjective): 모든 출력이 적어도 하나의 입력과 연결된 사상.
- 전단사(Bijective): 단사이면서 동시에 전사인 사상.
변환 행렬(Transformation Matrix): 선형 변환을 행렬 곱으로 나타낸 것이다.

2.8. 아핀 공간(Affine Spaces)

아핀 공간은 벡터 공간의 확장된 개념으로, 원점을 고정하지 않은 공간이다. 벡터 공간과 달리 평행 이동이 가능하다.

yourjin

make it mine, make it yours

이전 포스트