b-tree
b-tree는 다음의 3가지 키워드를 가진다.
균형잡힌, 다진트리, 외장검색트리
-
균형잡힌
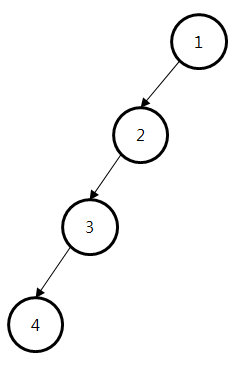
이진 탐색트리의 경우 균형이 한쪽으로 쏠리는 경우 최악의 탐색복잡도인 O(logN)을 가지게 된다. b-tree는 왼쪽 서브트리와 오른쪽 서브트리의 균형을 유지하도록 하여 적정 깊이를 유지한다.
-
다진트리
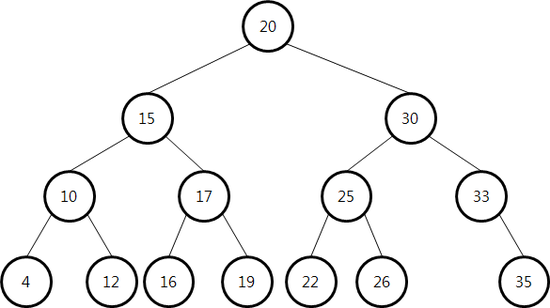
이진트리와 다르게 b-tree는 하나의 노드에 여러 key를 담을 수 있다. 이러한 구조는 적은 depth를 가질 수 있도록 하며, 참조포인터를 거치는 횟수를 줄여준다. 최종적으로 디스크 접근 횟수를 줄이게 된다.
- 외장검색트리
외장검색트리란 메모리가 아니라 디스크 상에 검색색인을 올려놓고 사용한다는 것이다. 메모리에 비해 디스크 접근은 매우 많은 비용을 소모한다. 따라서, 디스크 접근횟수를 줄일 수 있는 b-tree의 특성은 외장검색트리에 적합하다.
b-tree의 개념
- 좌우균형을 유지하는 트리로, 이진트리의 단점을 극복 가능
- 이진트리와 다르게 한 노드에 여러 key 저장 가능
- 최대자식노드 개수가 M개일 때, M차 b-tree라고 한다.
b-tree의 특징
- 부모노드의 key의 개수+1 만큼 자식노드를 가져야함
- 최대 자식수가 k일때 최대 key개수는 k-1 최소 키개수는 (k-1)/2
따라서 최소 자식수는 (k-1)/2+1 - leaf노드는 모두 같은 레벨에 있다.
- 노드에 여러 key는 정렬되어 있다.
- 입력자료에 중복은 없다.
b-tree의 검색, 삽입, 삭제 시간복잡도
검색복잡도
아래 그림에서 k진 분류시 depth는 이다.
depth는 곧 검색 복잡도이므로, k진 분류의 검색 복잡도도 이다.
그런데, b-tree의 최소분지수, 즉 최소 자식수는 (k-1)/2+1 이다.
따라서 최악의 검색복잡도는 즉 복잡도를 가지게 된다.
삽입복잡도
삽입 위치를 찾는데에 O(logN), 삽입시 오버플로우 발생시 최악의 경우 재분배가 루트노드까지 이뤄질 수 있기 때문에 O(logN) 대략 2*O(logN)는 O(logN)로 판단
삭제복잡도
삭제 위치를 찾는데에 O(logN), 삭제시 언더플로우 발생시 최악의 경우 재분배가 루트노드까지 이뤄질 수 있기 때문에 O(logN) 대략 2*O(logN)는 O(logN)로 판단
b-tree의 검색
루트노드에서부터 아래로 찾으려는 key를 찾는다.
- 루트노드의 key를 순서대로 탐색
- 맞는 위치의 자식노드로 내려가기
- key를 순서대로 탐색
- 자식노드로 내려가기
3, 4를 재귀적으로 반복하며 검색
b-tree의 삽입
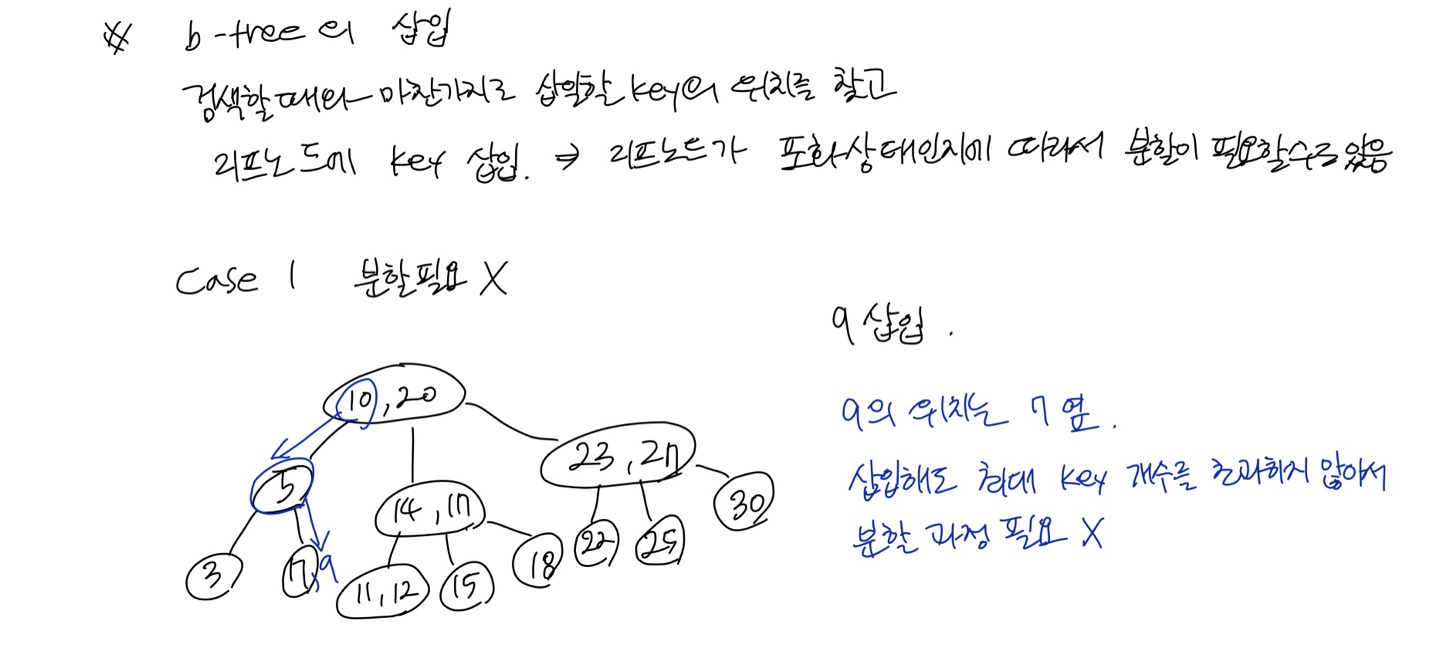
Case 1. 분할이 필요하지 않은 경우
삽입해도 최대 key개수를 넘지않아 그냥 위치만 잘 찾아 삽입하면 된다.
Case 2. 분할이 필요한 경우
삽입하면 최대 key개수를 넘어 분할이 필요한 경우
- 일단 삽입 후
- sibling 노드로 key를 넘길 수 있으면
재분배 - sibling 노드로 넘길 수 없다면 중앙값을 부모노드로 올린다.
*재분배란 key값을 바로 옆 노드로 보낼 수 없으니까 옮길 노드를 부모노드로 올리고 부모노드를 sibling node로 보내는 것
위 과정을 재귀적으로 반복한다.
아래 예시는 13을 삽입하는 것이다.
13을 sibling node로 넘기기 위해 재분배 과정을 거치고 있다.
아래 예시는 중앙값을 부모노드로 올리는 예시이다.
b-tree의 삭제
두 가지 케이스가 있다. 세부 케이스는 아래에서 다루겠다.
- leaf 노드를 삭제하는 경우
- 내부 노드를 삭제하는 경우
- 용어 설명
predecessor : 왼쪽 자손에서 가장 큰 key값
successor : 오른쪽 자손에서 가장 작은 key값
Case 1. leaf 노드 삭제
Case 1.1 leaf 노드 삭제 + 삭제할 노드의 key가 최소 개수 이상
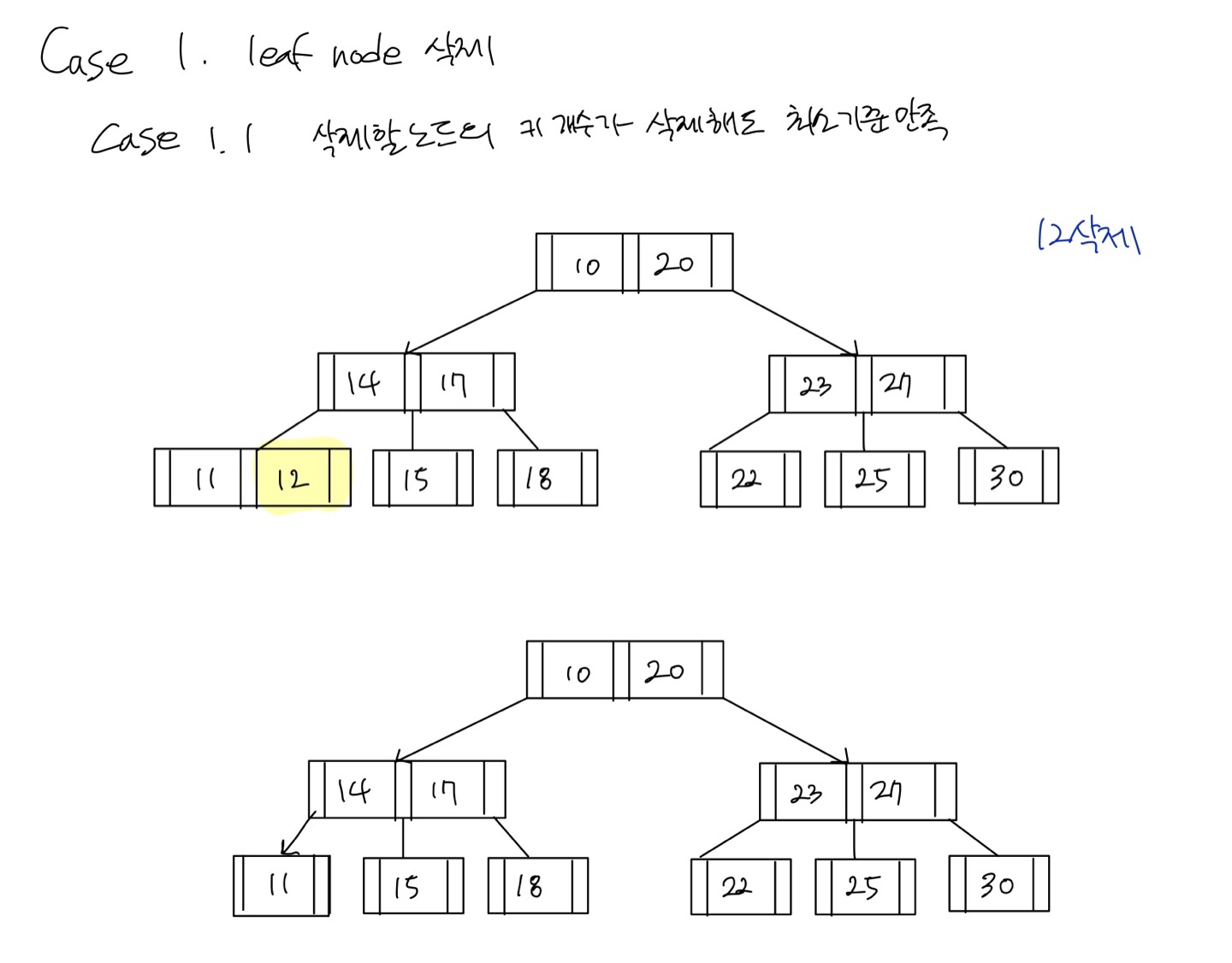12를 그냥 삭제하면 된다.
Case 1.2 leaf 노드 삭제 + 삭제할 노드의 sibling 노드가 최소개수 이상
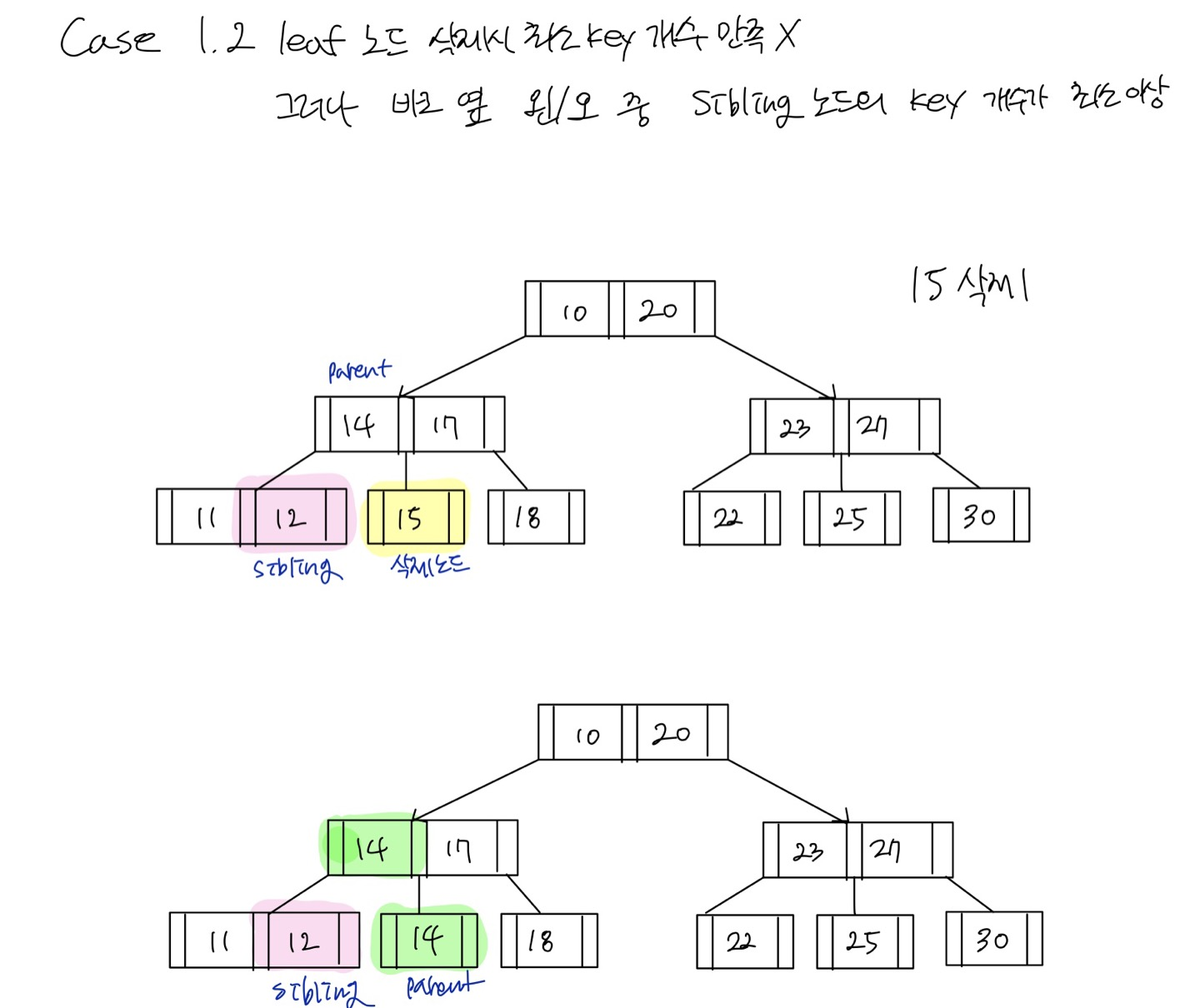
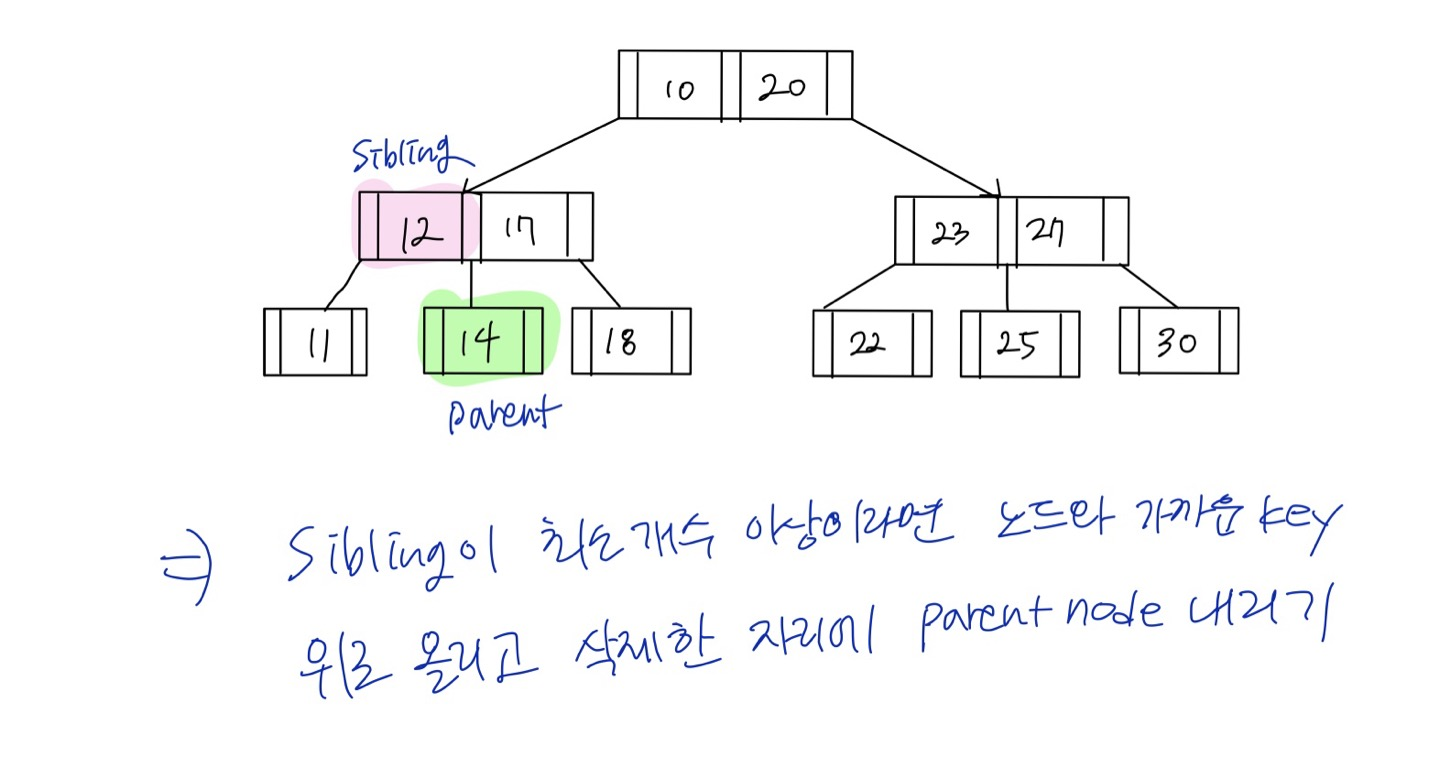sibling노드 위로 올리고 부모노드 삭제한 자리로 이동하는 재분배 과정을 실행한다.
Case 1.3 leaf 노드 삭제 + 삭제할 노드의 부모노드가 최소개수 이상
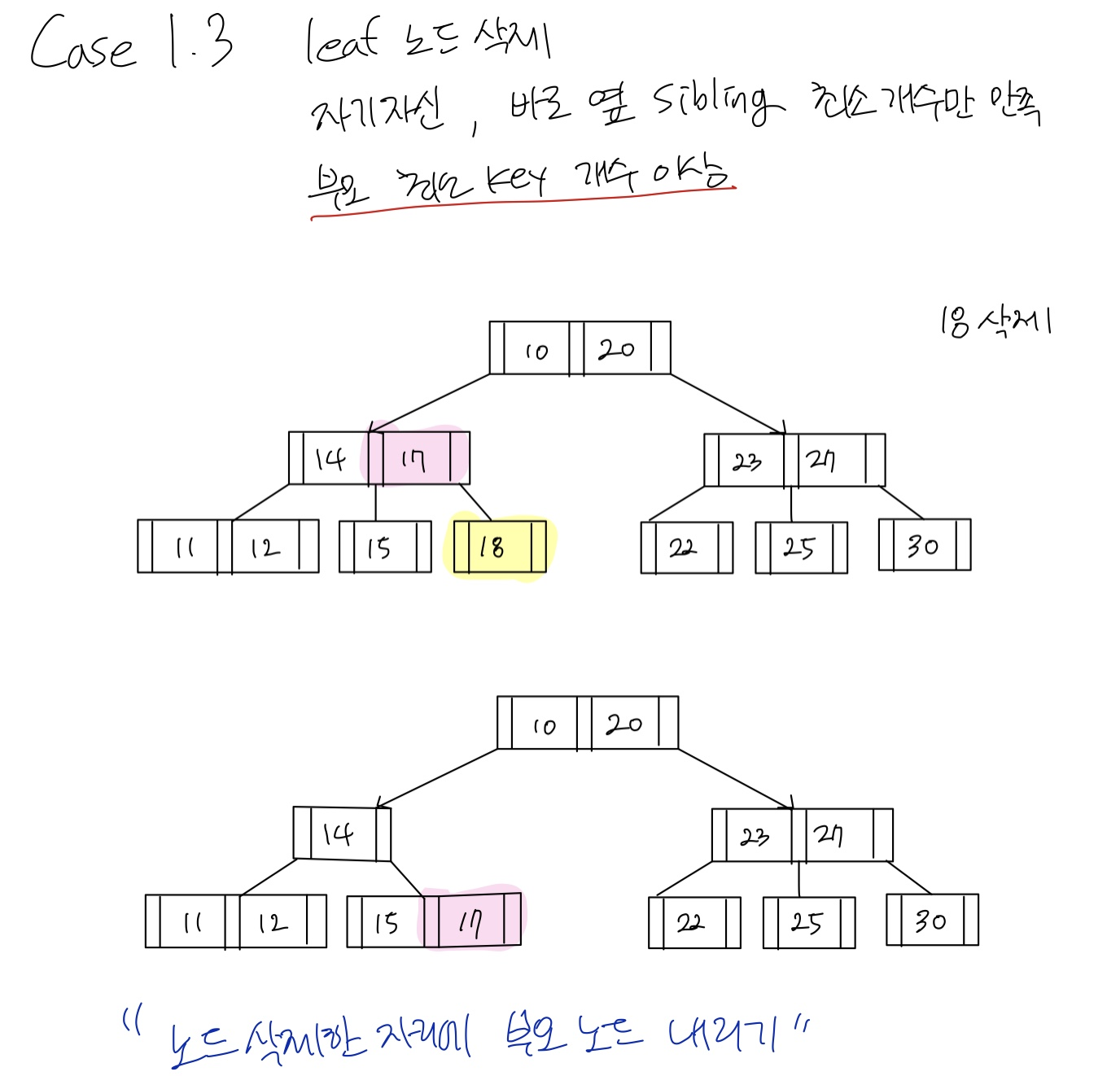부모노드 아래로 내리기
Case 1.4 leaf 노드 삭제 + 자기자신/sibling/부모노드 모두 최소개수만 만족
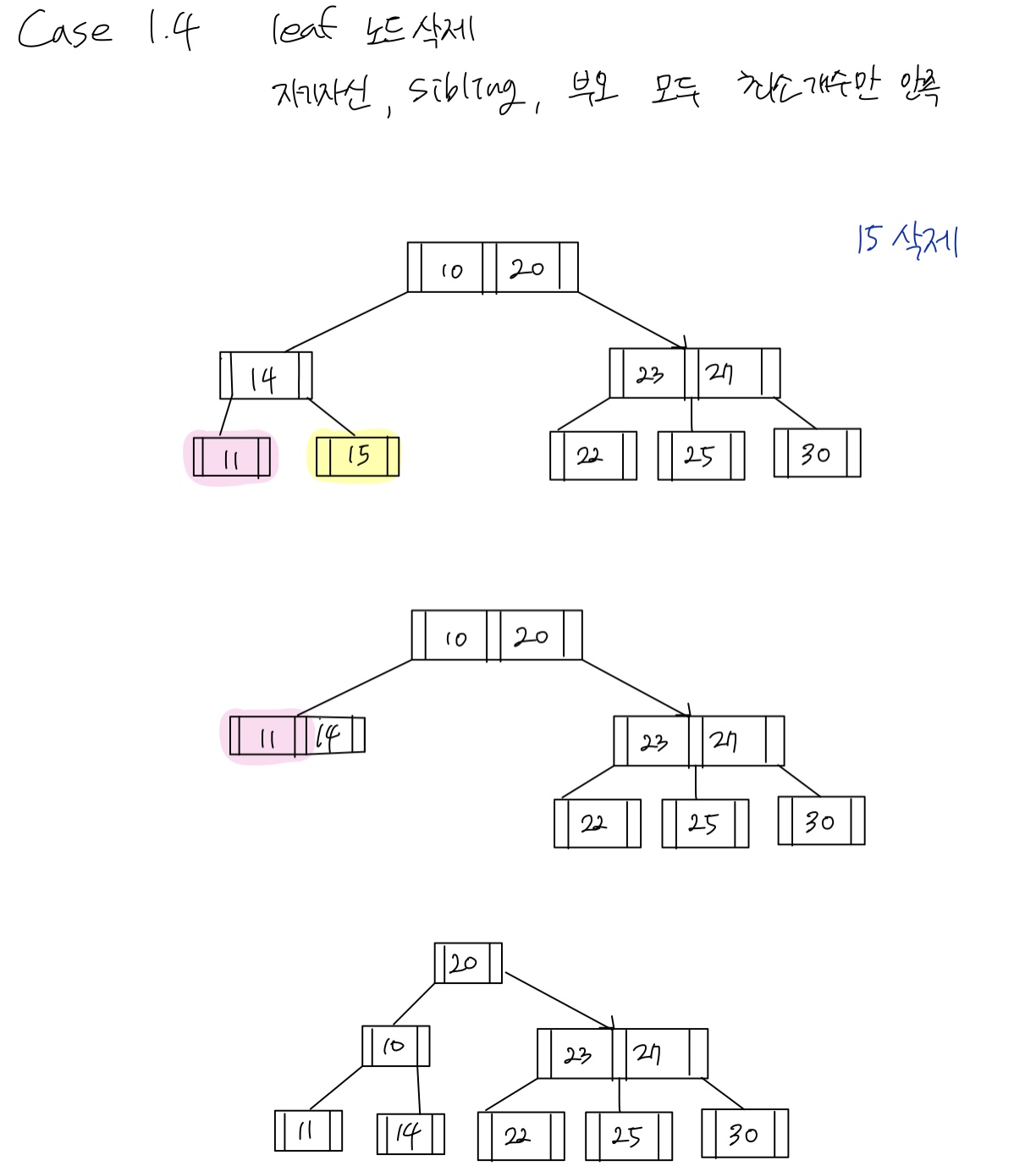
Case 2 내부노드 삭제
Case 2.1 내부노드 삭제 + 자기 자신 or 자식 노드가 최소 key 개수 이상
- predecessor or successor를 삭제한 자리에 대체
- predecessor or successor를 삭제한 이후는 case 1 leaf node삭제 과정과 동일한 과정 진행
2개의 예시를 통해 살펴보자
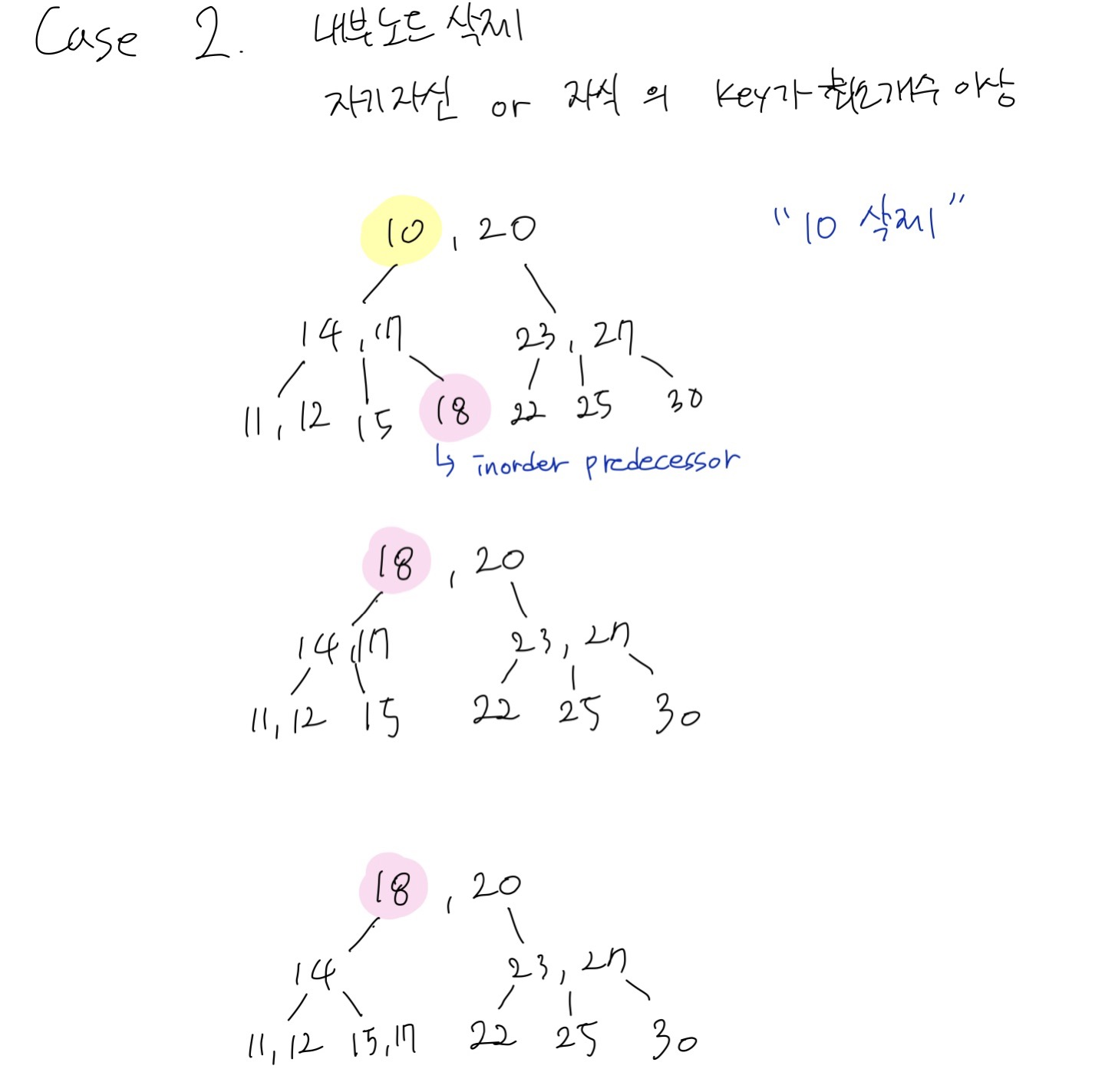
위 예시는 predecessor를 삭제한 자리에 대체하고
predecessor가 있던 자리에 predecessor의 부모노드를 내려오게 하는 과정이다.
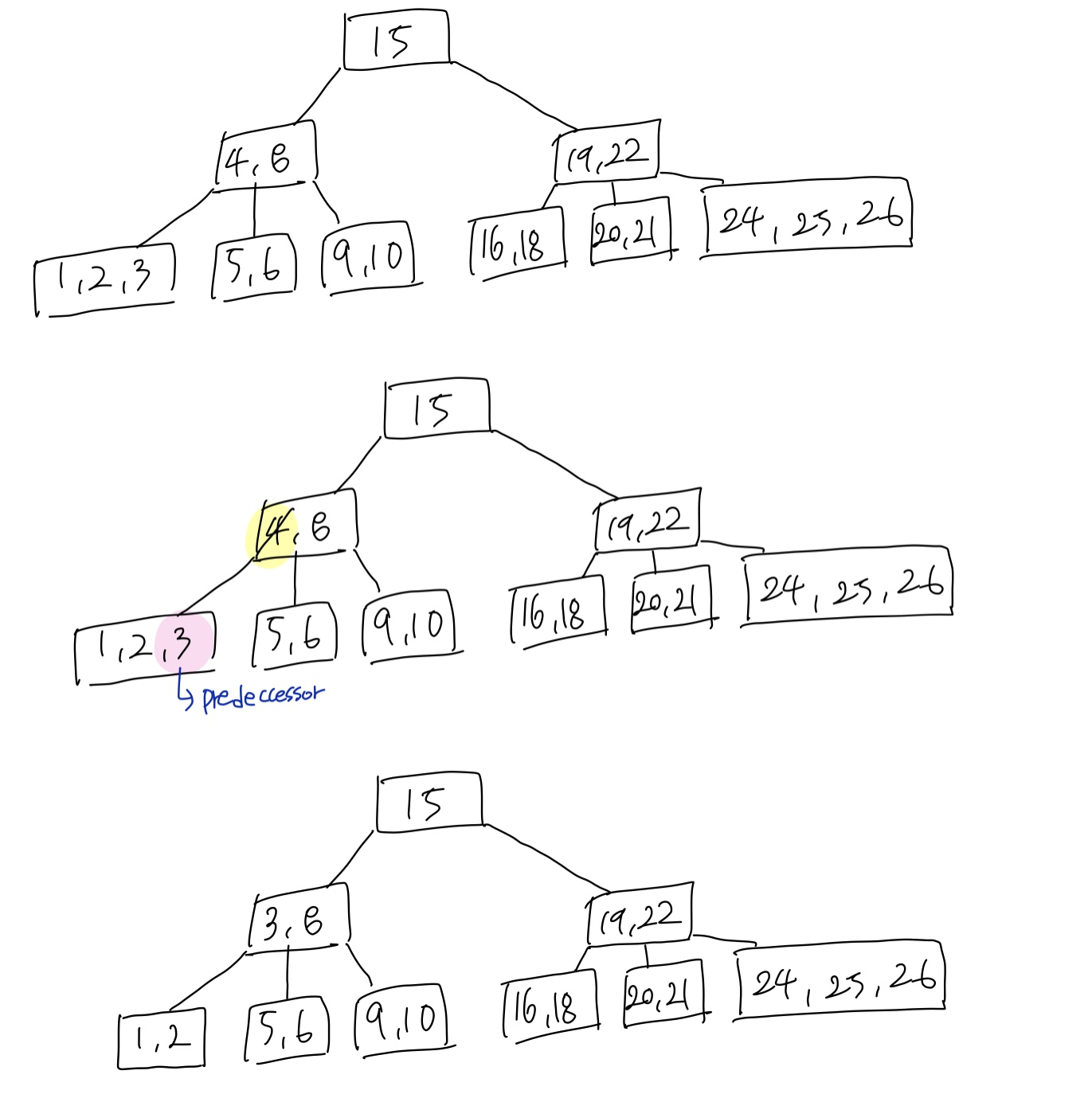
위 예시는 predecessor로 대체 후,
predecessor를 삭제하는 과정이다.
Case 2.2 내부노드 삭제 + 자기자신, 자식노드 모두 최소 key 개수
- k 삭제
- k의 자식 노드 병합 후 부모노드를 k의 sibling노드와 연결
- 이를 병합된 자식노드와 연결
뒤의 두 과정을 반복
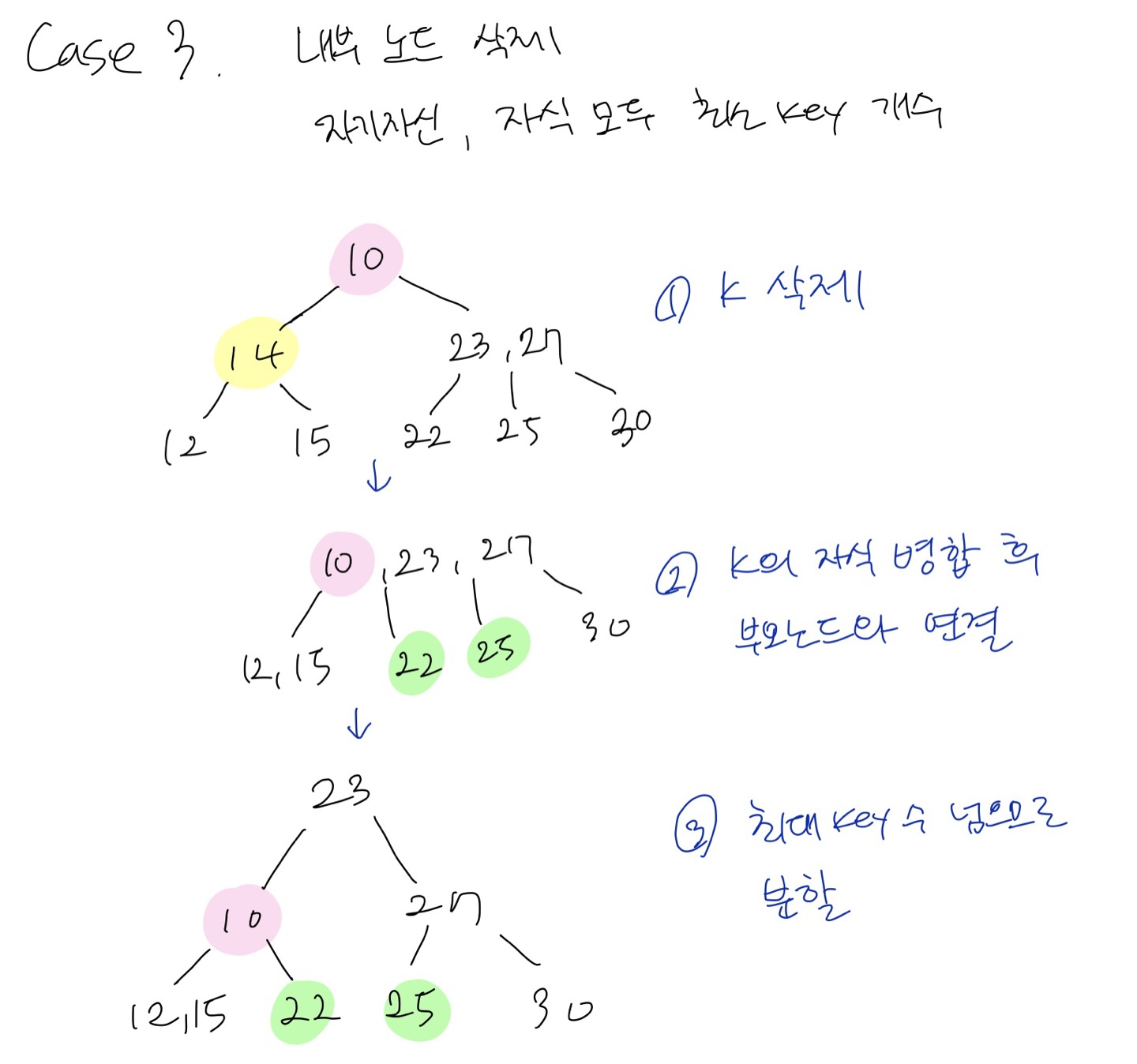
다른 예시
17 삭제
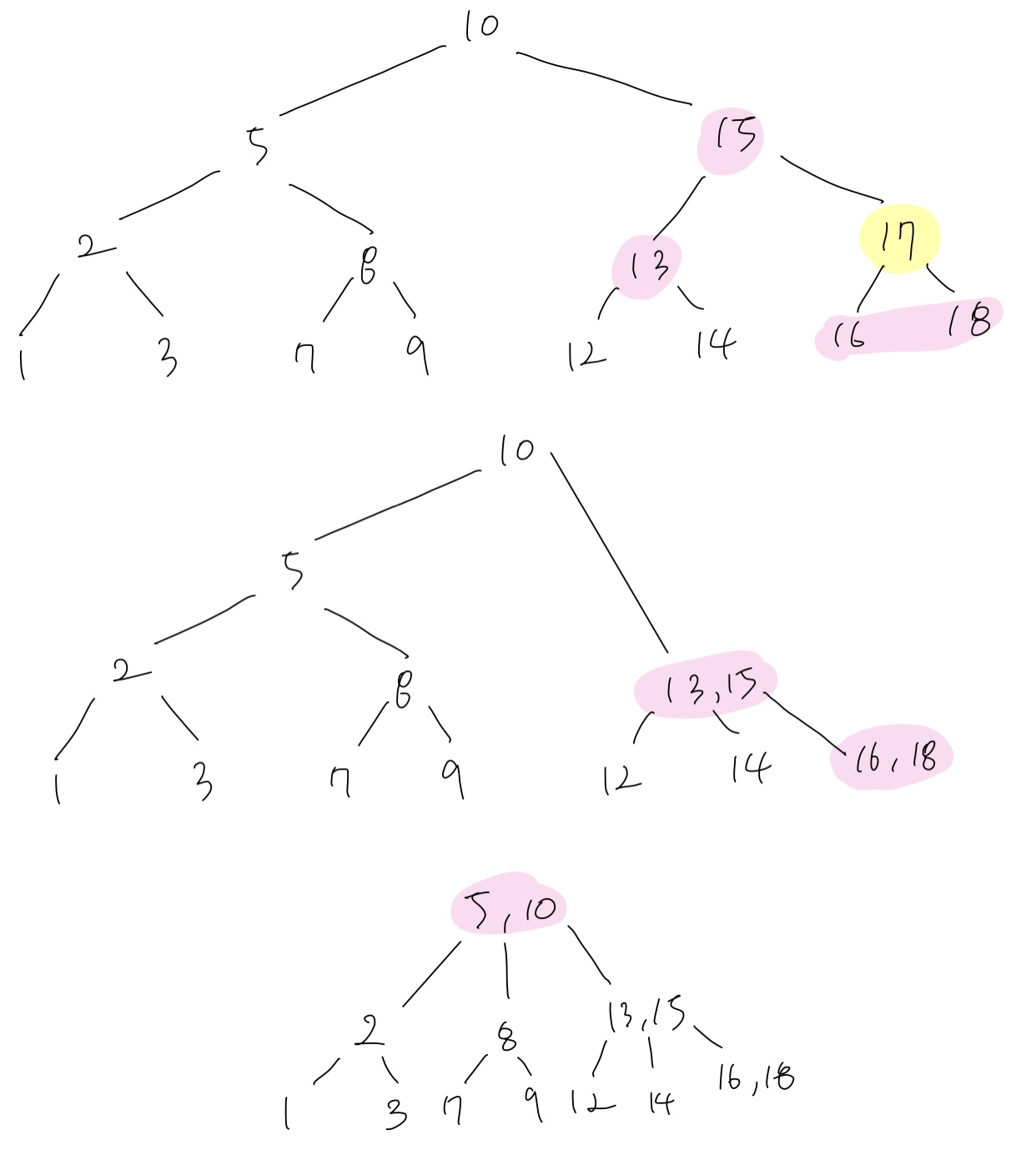
- 참고 자료
참고 자료 1
쉽게배우는 자료구조 with python 도서
