.png)
C4W1L02 Computer vision
Fully-connected layer, Convolution layer
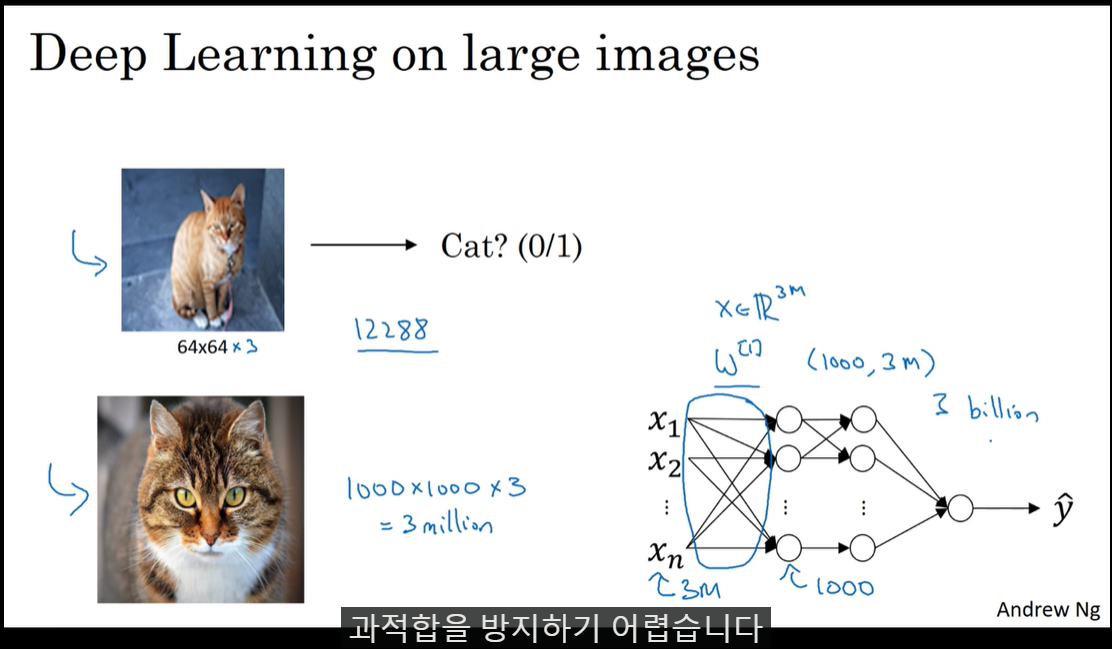
1000x1000x3 크기의 input, 1000개의 hidden node를 가지는 fc-layer를 생각해보면 3billion(30억)개의 parameter가 생긴다.
이는 과적합을 유도하기 쉽다.
이를 해결할 수 있는 것이 Convolution network이다.
convolution network는 인풋에 동일한 가중치(filter)를 슬라이딩하면서 적용한다. 이는 parameter의 숫자를 훨씬 줄여줄 수 있다.
C4W1L02 Edge Detection Examples
vertical edge detection
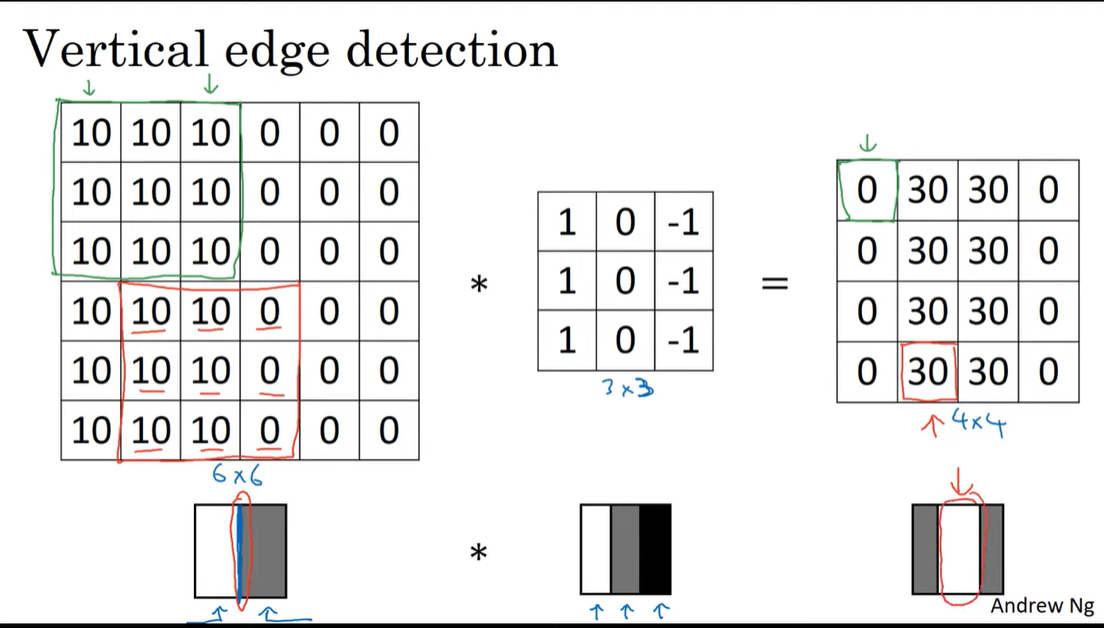
convolution network에서 vertical edge를 추출하려면 어떻게 해야할까?
아래와 같이 1, 0, -1 로 이루어진 filter를 사용하면 된다. 이 필터가 어떻게 vertical edge를 잘 잡아낼 수 있는 것일까?
직접 계산해보면 아래와 같다.
아래의 예시의 input은 한쪽은 밝고, 다른 한쪽은 어둡다.
이를 1, 0, -1 로 이루어진 필터와 합성곱하면 input에서 가운데 경계선 부근이 추출됌을 볼 수 있다.
경계선에 비해 꽤 넓은 범위로 추출된 것 같지만 이는 매우 작은 인풋이라 그런것이고 더 큰 이미지에 적용한다면 정밀하게 추출될 수 있다.
C4W1L03 More Edge Detection
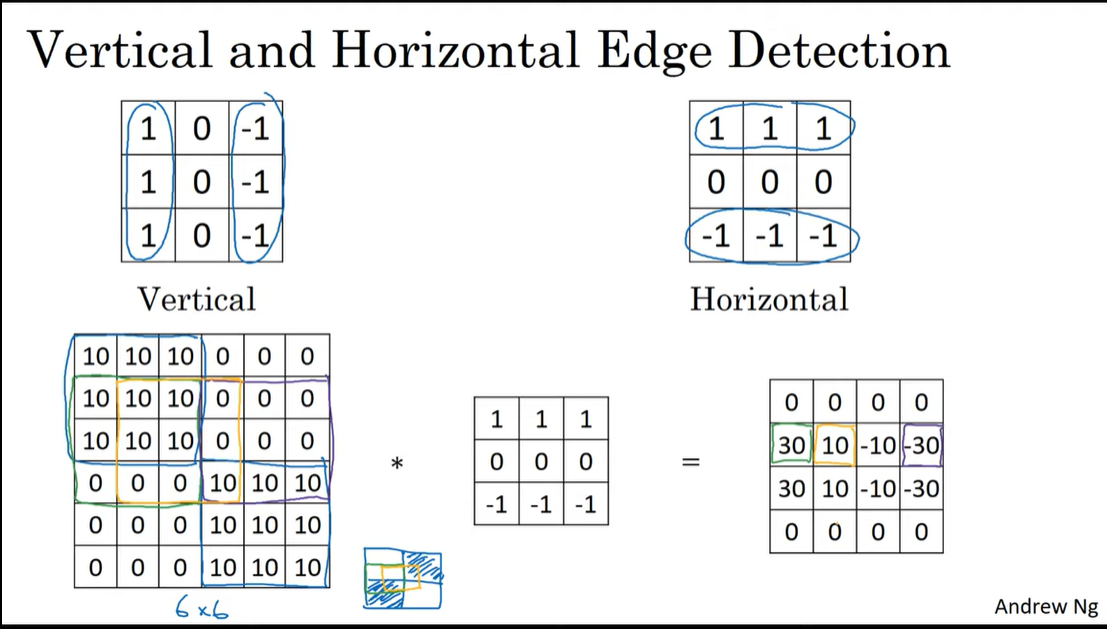
Vertical and Horizontal Edge Detection
밝은 부분 -> 어두운 부분의 edge는 양수로,
어두운 부분 -> 밝은 부분의 edge는 음수로 나오게 된다.
방향성을 고려하지 않는다면 결과에 절댓값을 씌어줄 수도 있다.
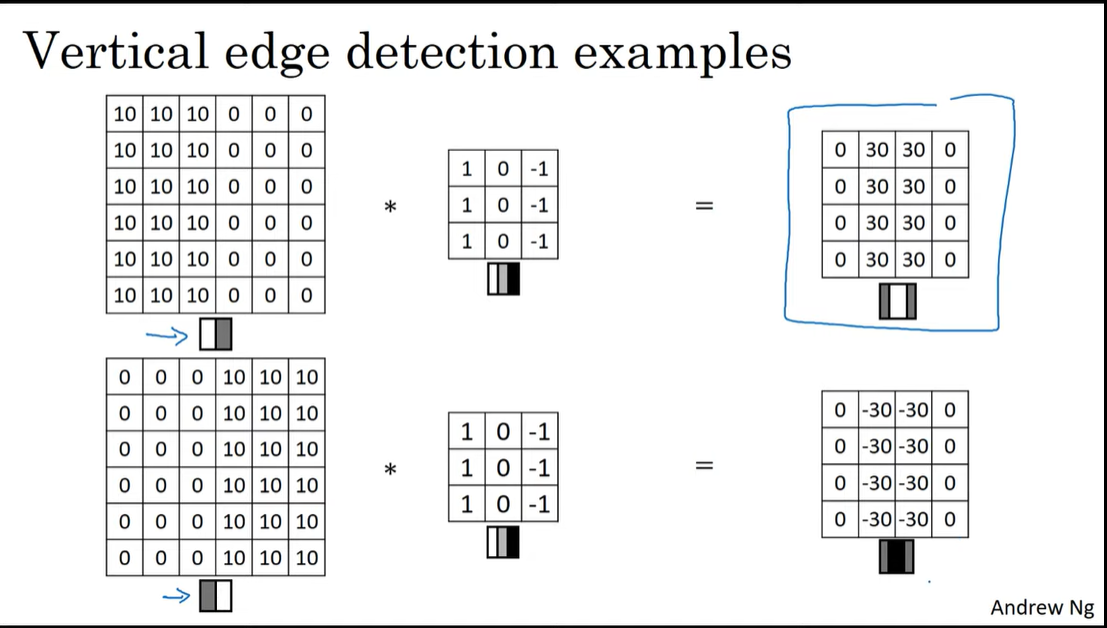
horizontal edge를 추출하려면 위의 vertical filter와 같은 원리로 아래와 같이 구성하면 된다.
초록색 박스부분에선 input에서 10에서 0으로 바뀌는 경계선 부분에 해당하기 때문에 feature map에서 30이 나오고,
보라색 박스부분에선 input에서 0에서 10으로 바뀌는 경계선 부분에 해당하기 때문에 feature map에서 -30이 나온다.
노란색 박스부분에선 input에서 대체적으로 10에서 0으로 바뀌지만 다른 한쪽에 10 포함되어 있기 때문에 30보다 작은 10이라는 숫자가 나오게 된다.
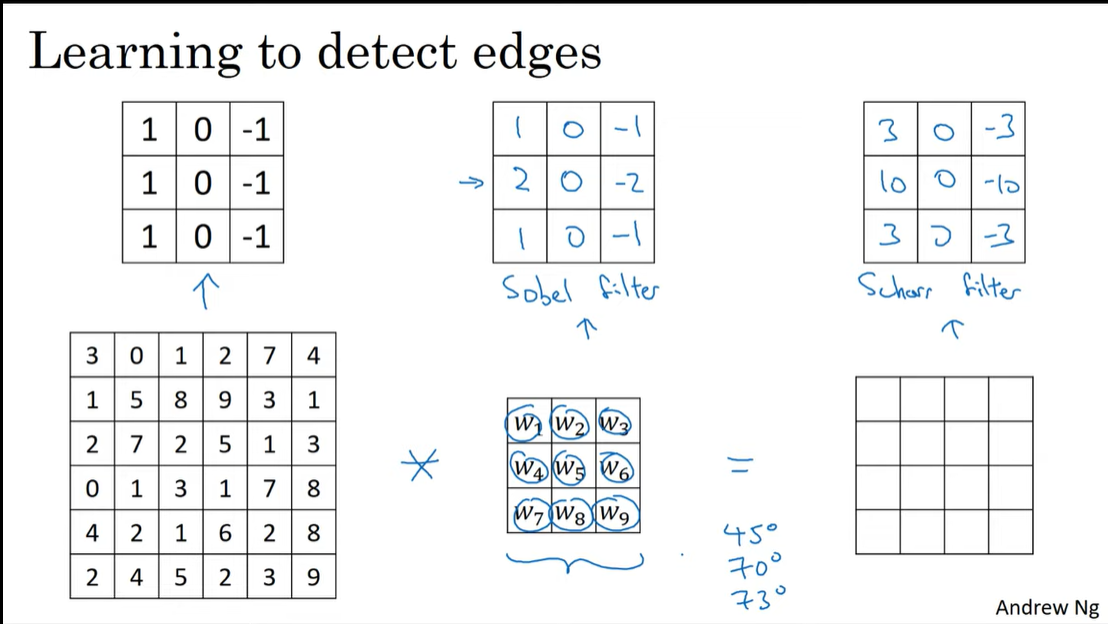
Learning to detect edges
앞선 예시에서의 vertical filter, horizontal filter 모두 하나의 예시이다.
아래의 sobel filter, schor filter 처럼 중간에 큰값을 줘서 중간 픽셀을 더 집중할 수도 있다.
하지만 이런 수작업으로 만든 특정 filter보다,
filter를 파라미터로하여 역전파를 통해 학습하는 것은 아주 다양한 edge를 검출해낼 수 있게한다.
Q. 정사각형 input이 아니라 직사각형 input을 넣는 경우도 있는가?
참고링크
있다. 정사각형 input을 사용하는 것은 계산의 편리함을 위해서이다.
만약 input이 224x320라면 pooling layer를 적용함에따라 224x320, 112x160, 56x80, 28x40, 14x20, 7x10 와 같이 변화할 것이다.
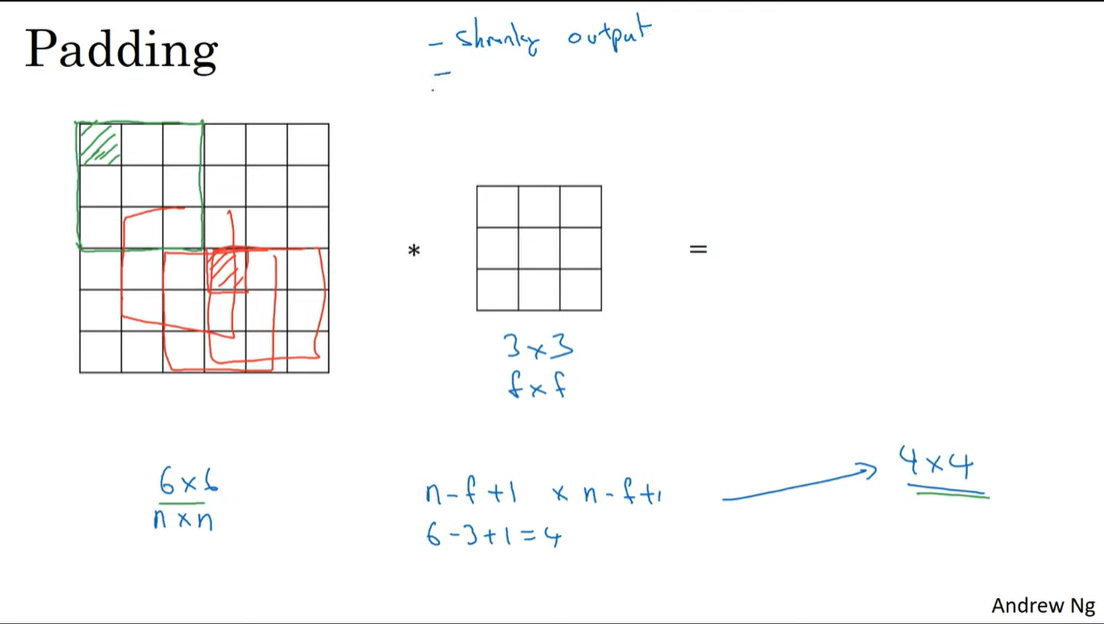
C4W1L04 Padding
padding
convolution layer에서 패딩이 필요한 이유는 두가지이다.
- convolution연산을 할 수록 feature map의 크기는 작아진다. 여러 layer를 거치고 난 후에는 아주 작은 map만 남게된다.
- 가장자리의 input은 결과에 사용되는 횟수가 적다.
아래 그림에서 초록색 픽셀은 한번만 연산되는 반면 빨간색 픽셀은 여러번 연산되는 것을 볼 수 있다.
Valid and Same convolutions
- valid
no padding.
input : n x n
filter : f x f
output : n-f+1 x n-f+1
- same
input shape == output shape
input : n x n
filter : f x f
output : n+2p-f+1 x n+2p-f+1
위의 식에 따라서 input shape과 output shape이 같으려면 p = (f-1)/2 가 된다.
따라서 filter가 홀수라면 위의 식에 따른 padding을 적용시 conv연산을 하더라도 동일한 크기를 유지할 수 있다.
이는 filter의 크기를 짝수로 쓰지 않는 이유와도 관련이 있다.
- filter가 짝수라면 padding이 왼쪽과 오른쪽이 비대칭적으로 적용이 되어야 한다.
- filter가 짝수라면 중앙을 나타내는 픽셀이 없어서 계산을 할 때 애매하다.
짝수 filter가 성능에 큰 영향을 주진 않지만 적용할 때 깔끔해지지 않기 때문에 관습적으로 사용하지 않는다고 한다.

C4W1L05 Strided Convolutions
Strided convolution
convolution에서 stride가 2라면 아래 그림처럼 2칸씩 옮기며 연산을 진행한다.
따라서 앞서 output shape이 (n+2p-f) + 1 이었다면 stride가 적용된다면
(n+2p-f)/s + 1 가 된다.
그런데 만약 이 값이 정수가 아니라면 내림을 해준다. 내림을 한다는 의미는 아래 그림에서 파란 박스처럼 input 영역을 벗어나게 되는 경우는 연산을 하지 않는다는 것이다.

Q. stride를 크게 줄수록 정보의 손실이 일어나지 않는가?
맞다. 정보의 손실이 일어난다. 하지만 손실이 허용될 때가 있다. 예를 들어 대부분이 까맣고 일부분만 하얀 밤하늘의 별과 같은 이미지가 있다고 하면 stride를 작게주어 세밀하게 학습하는 것보다 stride를 크게 줘서 학습을 해도 feature는 잘 추출될 수 있을 것이다.
Technical note on cross-correlation vs convolution
딥러닝을 공부하다보면 우리가 흔히 말하는 convolution이라는 것이 사실 convolution이 아니라고 하는 것 을 볼 수 있다.
사실 수학, 신호처리에서 말하는 convolution은 곱하는 연산과 더하는 연산을 해준다음, 그것을 가로, 세로로 뒤집는 미러링 과정을 진행한다. 미러링 과정을 통해 결합법칙이 성립하게 해주기에 이 과정이 중요하다고 한다.
딥러닝에서는 미러링 과정을 생략하여도 학습에 아무런 문제가 없기 때문에 미러링을 생략한 형태의 convolution을 관습적으로 convolution이라고 부른다.

C4W1L06 Convolutions Over Volumes
Convolution on RGB images
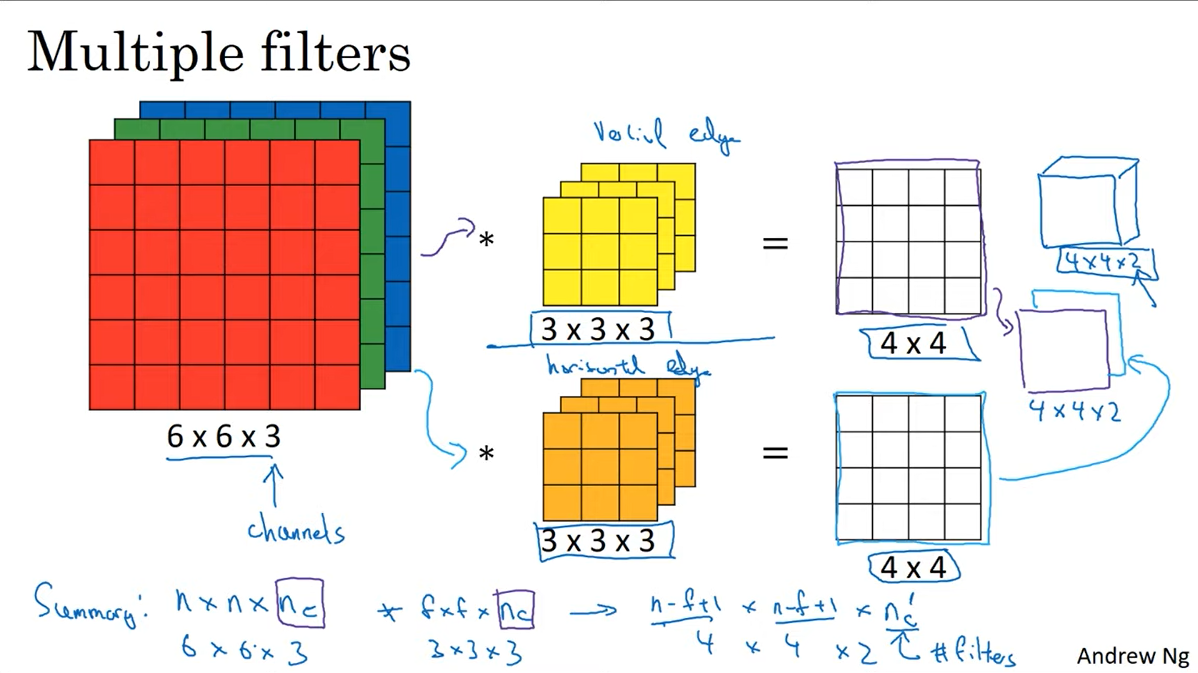
covolution을 텐서에 적용하는 방법은 아래 그림과 같다.
input channel수와 동일한 수의 channel을 가지는 filter로 합성곱을 하면 된다. 결과로는 1차원의 map이 나오게 된다.
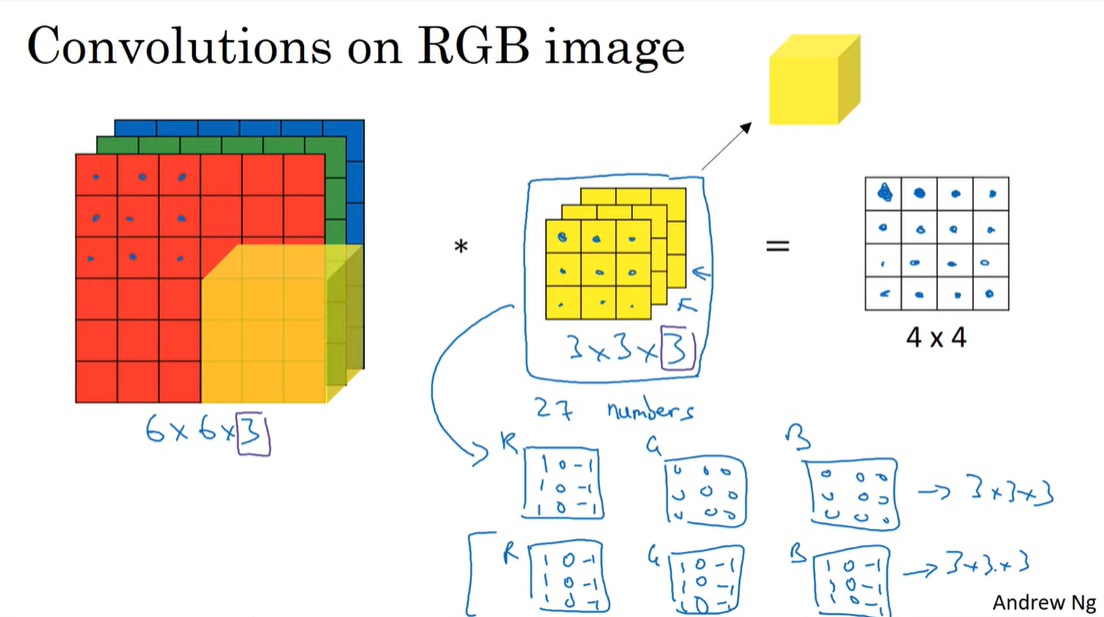
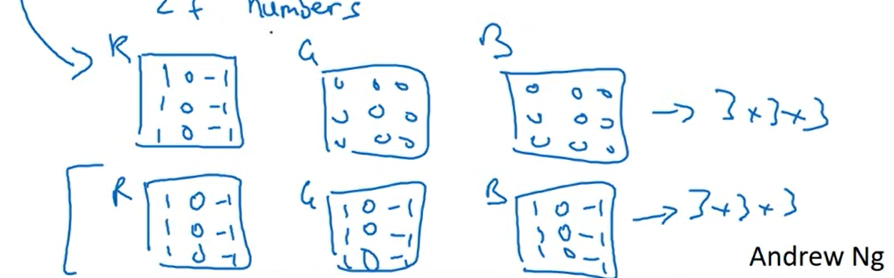
이때 filter를 아래 그림의 첫번째처럼 구성하게되면 R채널의 수직 성분을 추출할 것이고,
두번째처럼 구성하게되면 색깔에 상관없이 수직 성분을 추출할 것이다.
Multiple filters
필터를 여러개 적용한다면 필터의 개수만큼 다양한 종류의 특징이 추출될 것이다.
Classification 모델을 보면 channel을 많이 뽑고 보는 모델들이 있는데 이러한 이유로 다양한 feature들이 뽑힐 수 있어 성능의 향상이 있지 않았나 싶다.
여러개 필터를 적용한다면 output의 channel은 필터의 개수와 동일해질 것이다.
C4W1L07 One Layer of a Convolutional Net
이 장에서는 하나의 레이어에서 다음 레이어로 넘어갈 때 연산이 어떻게 진행되는지 설명한다.
필터를 적용한 결과에 activation func, bias를 추가하면 ouput의 한 채널이 완성된다.
이 과정을 filter의 개수만큼 진행하면 된다.
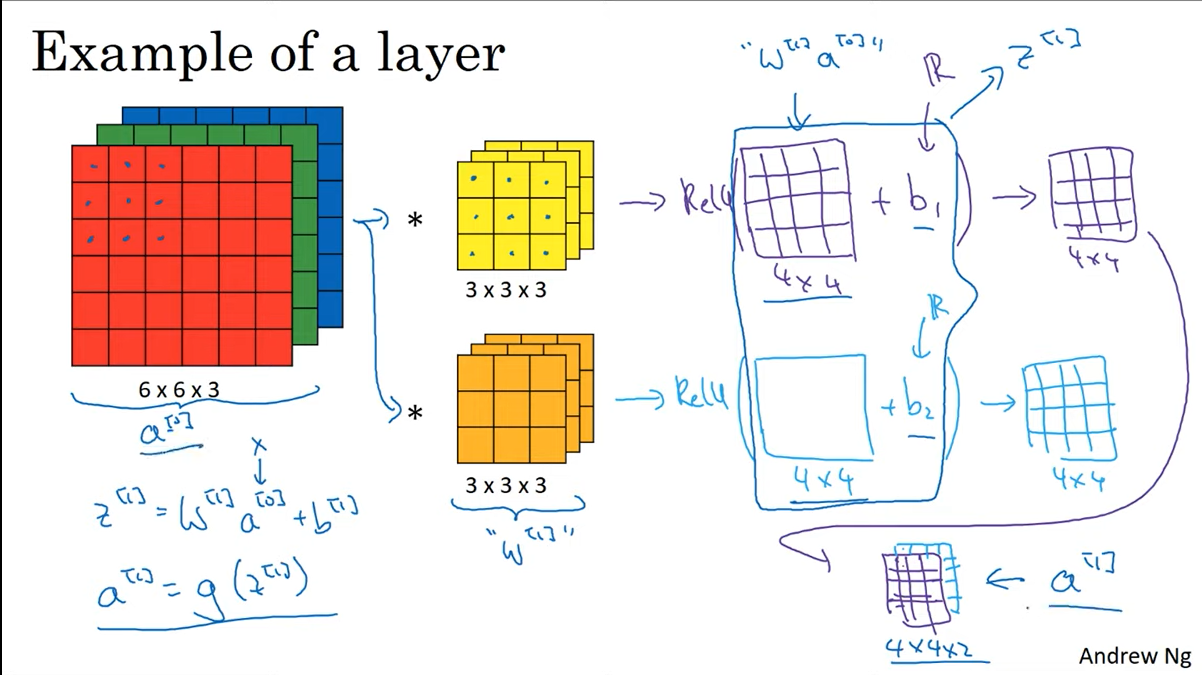
아래와 같은 표현이 등장하는데, [] 안에 들어가는 숫자는 몇번째 layer 인지를 나타내는 것이다.
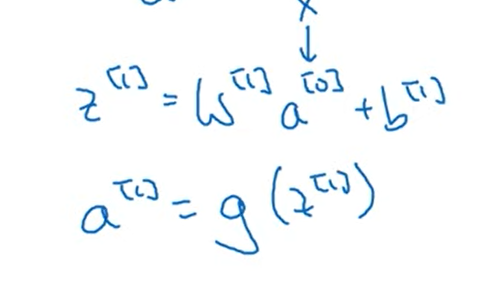
C4W1L09 Pooling Layers
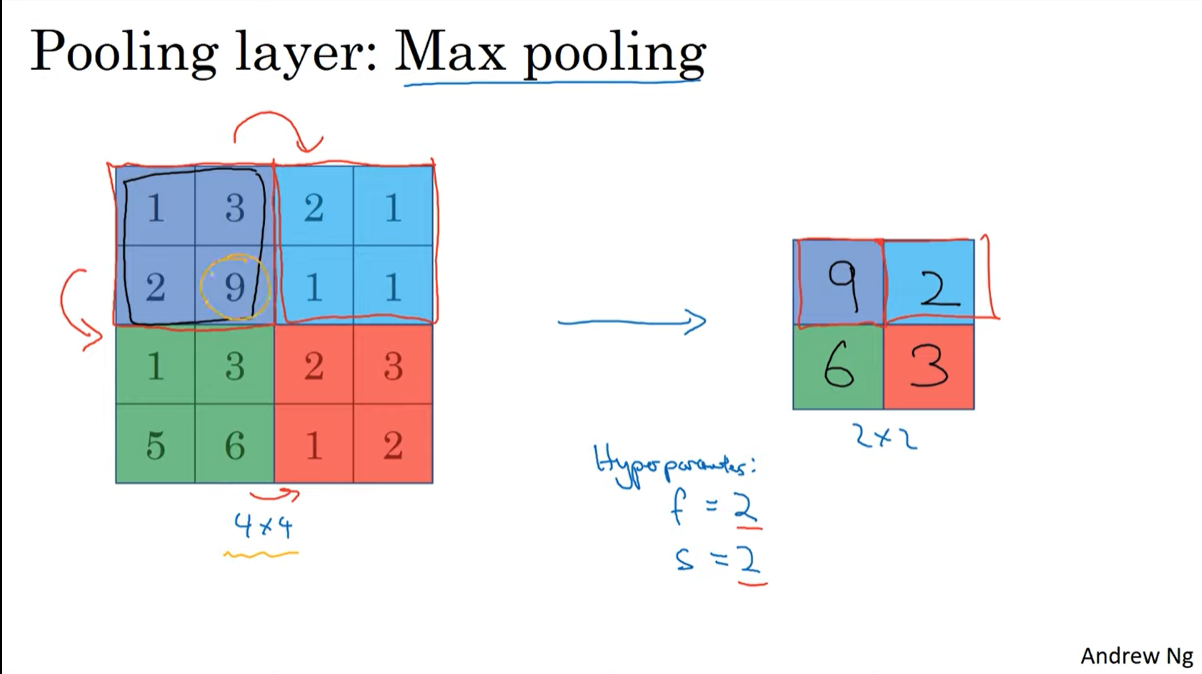
Max pooling
필터가 적용되는 영역에서 가장 큰 수만 뽑히는 연산이다.
pooling이 적용될때 output size를 계산하는 방법은 convolution할 때와 같다.
pooling layer에서의 hyperparameter는 f(filter), s(stride)이다. 2, 2로 두는 경우가 많다고 한다.
(n -f)/s + 1 이다. (channel은 conv연산에서는 filter의 개수였다면 pooling에서는 인풋의 채널과 같다)
pooling layer는 단순 연산만 하기에 학습하는 parameter가 없다.
pooling에서는 padding을 거의 쓰지 않는다고한다.
(그런데 테두리 부분에 max가 존재하는 경우라면 padding을 추가해주는 것이 좋지 않을까?)
Average pooling
거의 사용하지 않는다고 한다.
pooling의 목적이 특징을 극대화하려고 하는 것이기에 평균을 구해서 특징을 완화시키는 것은 도움이 안될 것 같다.
레이어 하단부에서 MAP(mean average pooling)가 사용되는 경우는 있다.
map는 grad cam에서도 사용된다.
C4W1L10 CNN Example
Neural Network example
LeNet-5
- input : 32 x 32 x 3
- conv + pooling , FC-layer , softmax
convolution 모델의 패턴
- 층이 깊어질수록 H, W 는 작아지고 channel은 늘어난다.
- conv - pooling 이 반복된 후 FC layer, softmax 가 이어지는 형태
Q. 왜 처음부터 채널의 수를 많이 뽑지않고 뒤로 갈수록 늘릴까?
초반에는 H, W가 크기에 연산량의 제약상 효율적으로 feature를 추출하기위해 그런것이라고 예상된다.
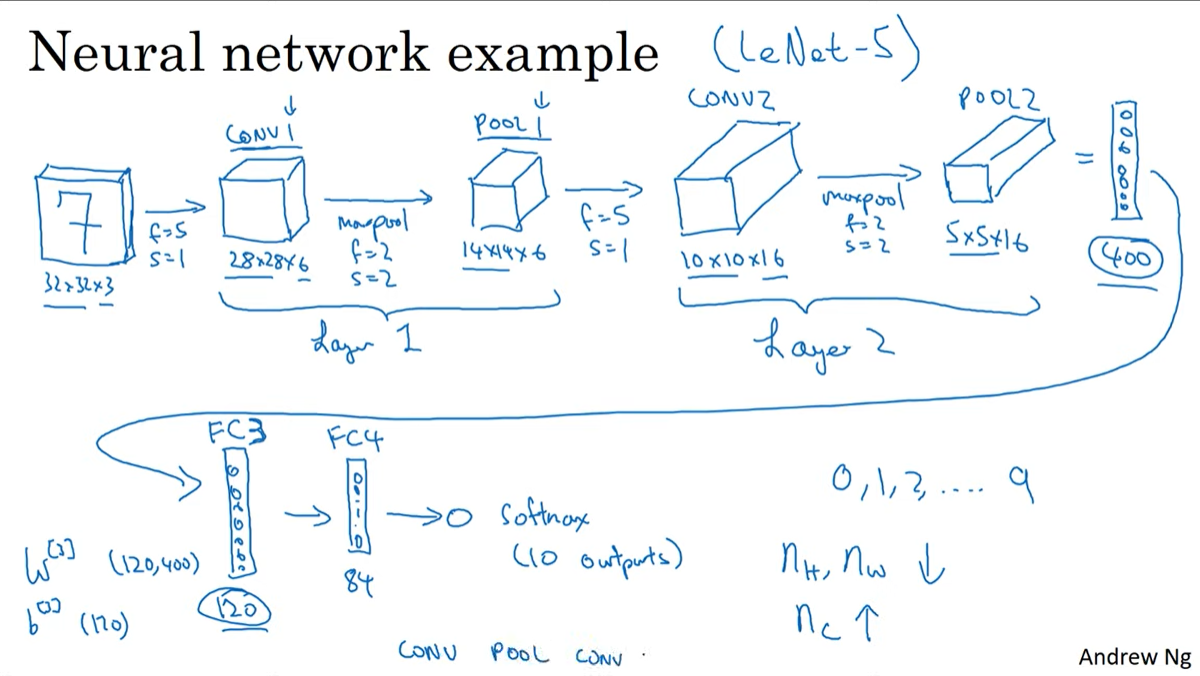
*층의 개수를 셀때는 conv+pooling을 하나의 레이어로 명칭한다.(하나의 convention)
아래는 LeNet-5의 구조이다.
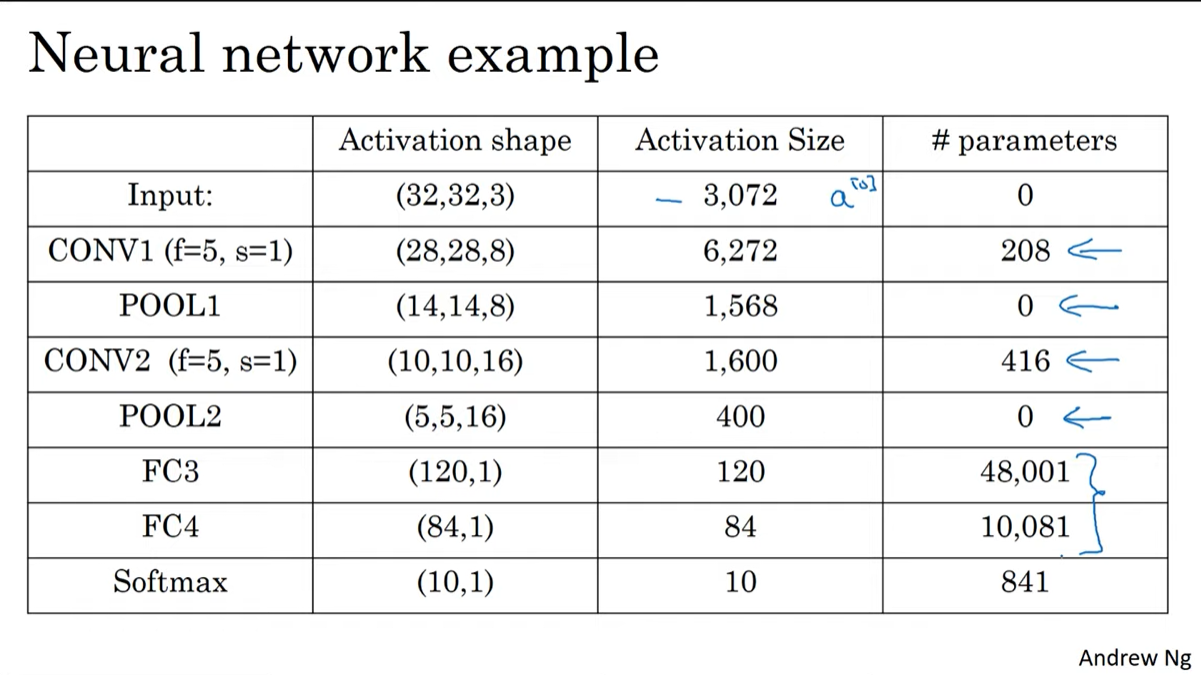
여기서 알 수 있는 것은
- activation size가 점진적으로 줄어든다. 너무 빠르게 감소하면 성능에 악영향을 줄 수 있다.
- conv layer가 dense layer에 비해 현저히 적은 파라미터를 가진다.
Q. 위의 사진의 parameter에서 channel을 생략한 것 같다.
맞다. 위의 사진에서 parameter를 계산할 때 필터의 channel을 1로 두고 계산하고 있는데, CONV1기준으로 정확하게 계산하면
((5x5x3)+1)x8 = 608 이 된다.
C4W1L11 Why Convolutions
Why convolutions
Parameter sharing
한 이미지 내에서 동일한 필터를 공유한다.
Sparsity of connection
아래 그림에서 output의 초록색 부분은 input의 초록색 박스 부분과만 연결된다. 빨간색 박스도 이와 같다. 이러한 특성으로 희소한 conneciton을 가지게 된다.
위의 두가지 특성으로 적은 파라미터수, 오버피팅 방지를 할 수 있다.
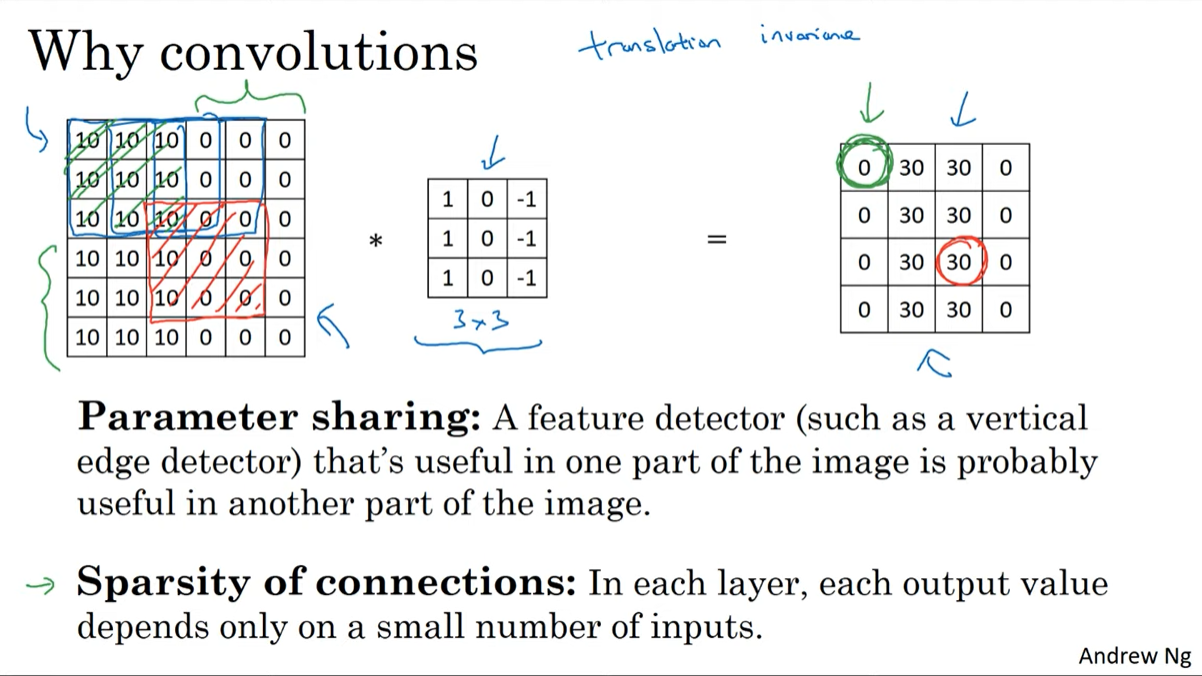
translation invariance
동일한 filter를 적용하기 때문에 이미지내 물체의 위치가 달라지더라도 특징을 포착해낼 수 있다.
위의 이유가 convolution이 효과적인 이유이다.
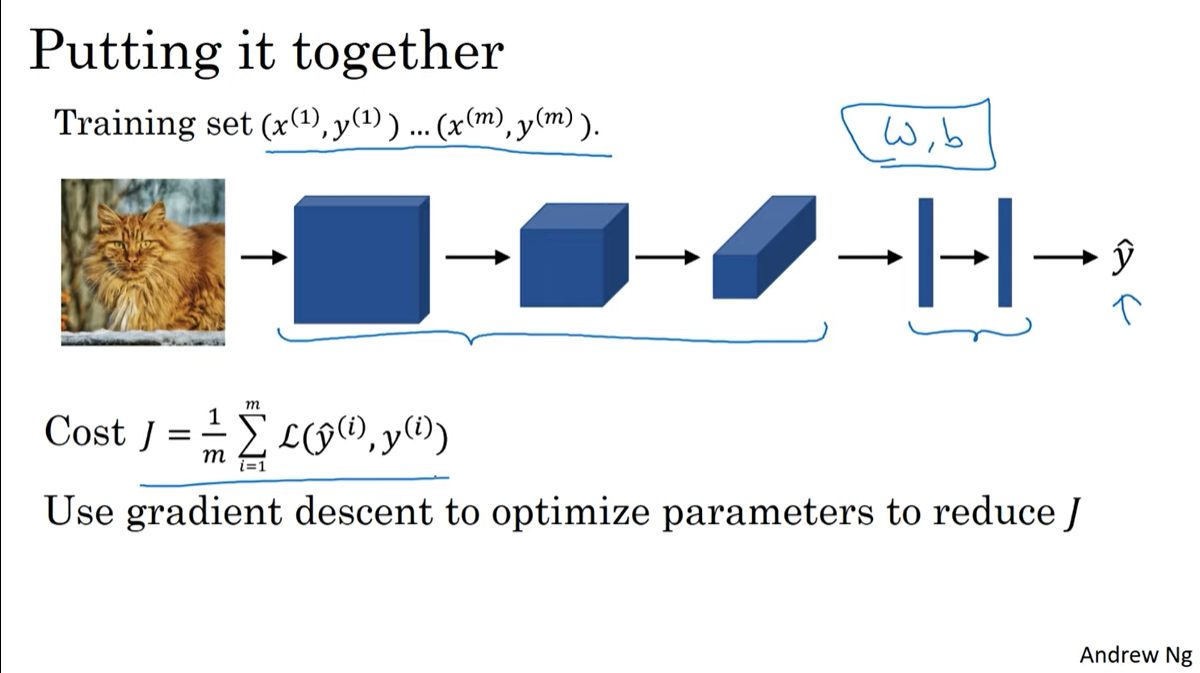
Putting it together
model의 예측치가 나오면 이의 오차를 합한 후에 training set 크기(m)로 나눠주면 cost가 나온다.
이 cost를 backpropagation하여 각 conv layer가 가지는 w, b를 업데이트하면된다.