PCA를 소개합니TADA~🎉

Feature selection vs Feature engineering

변수선택은 기존 변수를 어떠한 변형없이 중요한 변수만 골라내는 것을 의미합니다.

피쳐엔지니어링은 기존 변수를 토대로 새로운 변수를 만들어 내는 것입니다.

PCA

PCA는 피쳐엔지니어링 기법중에 하나라고 볼 수 있습니다.

Eigen-Value Decomposition

원리를 이해하기위해선 고유값분해, Eigen-Value Decomposition에 대해 알아야 합니다.

어떤 행렬 A와 어떤 벡터 x를 곱하면 상수값과 어떤 벡터x 형태로 나타낼 수 있는 경우가 있습니다.

Ax = λx
A를 곱했더니 방향은 같고, 크기만 달라진 것입니다.

여기서 x를 고유벡터(eigen vector), λ를 고유값(eigen value)라고 합니다.

이제 두 요소를 구해봅시다.

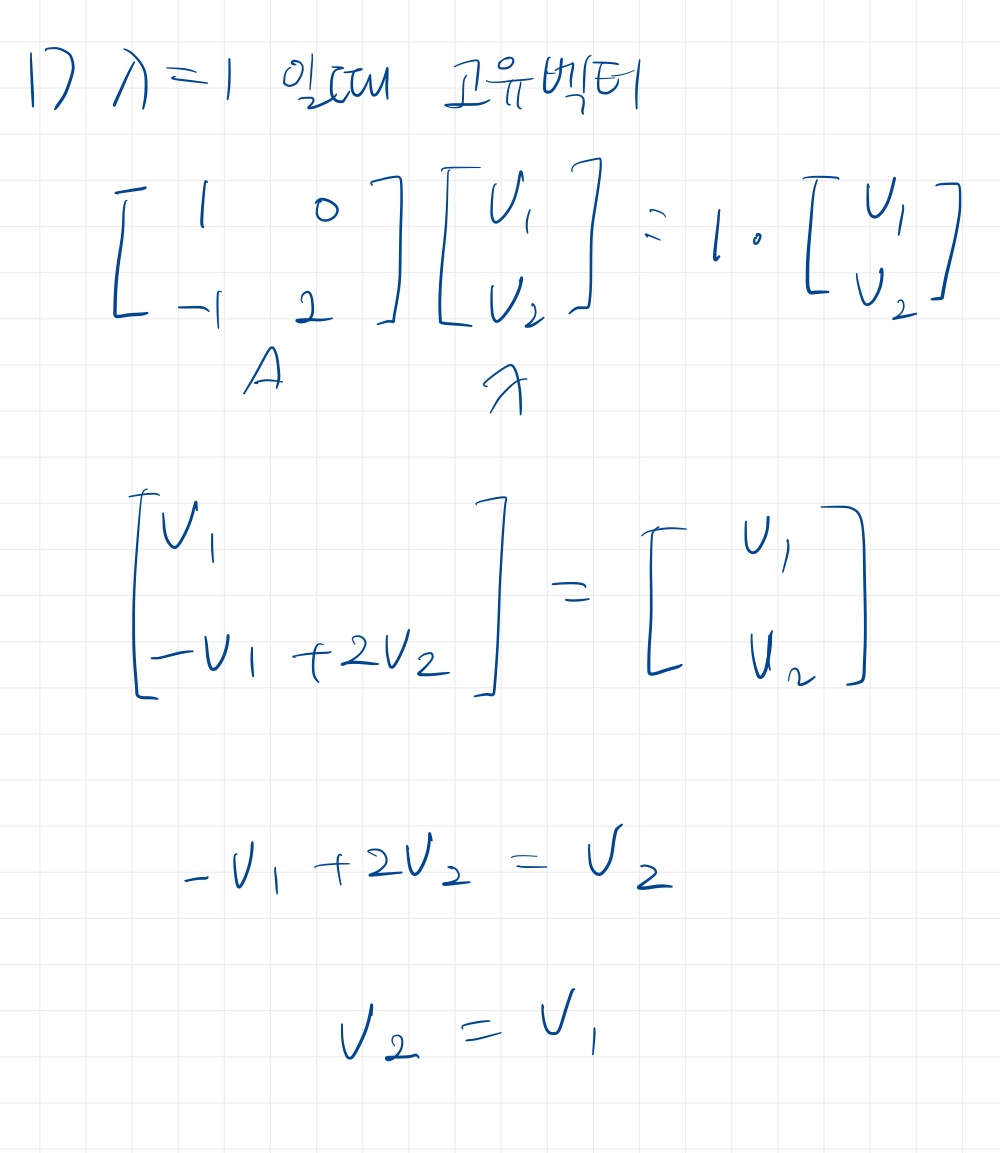
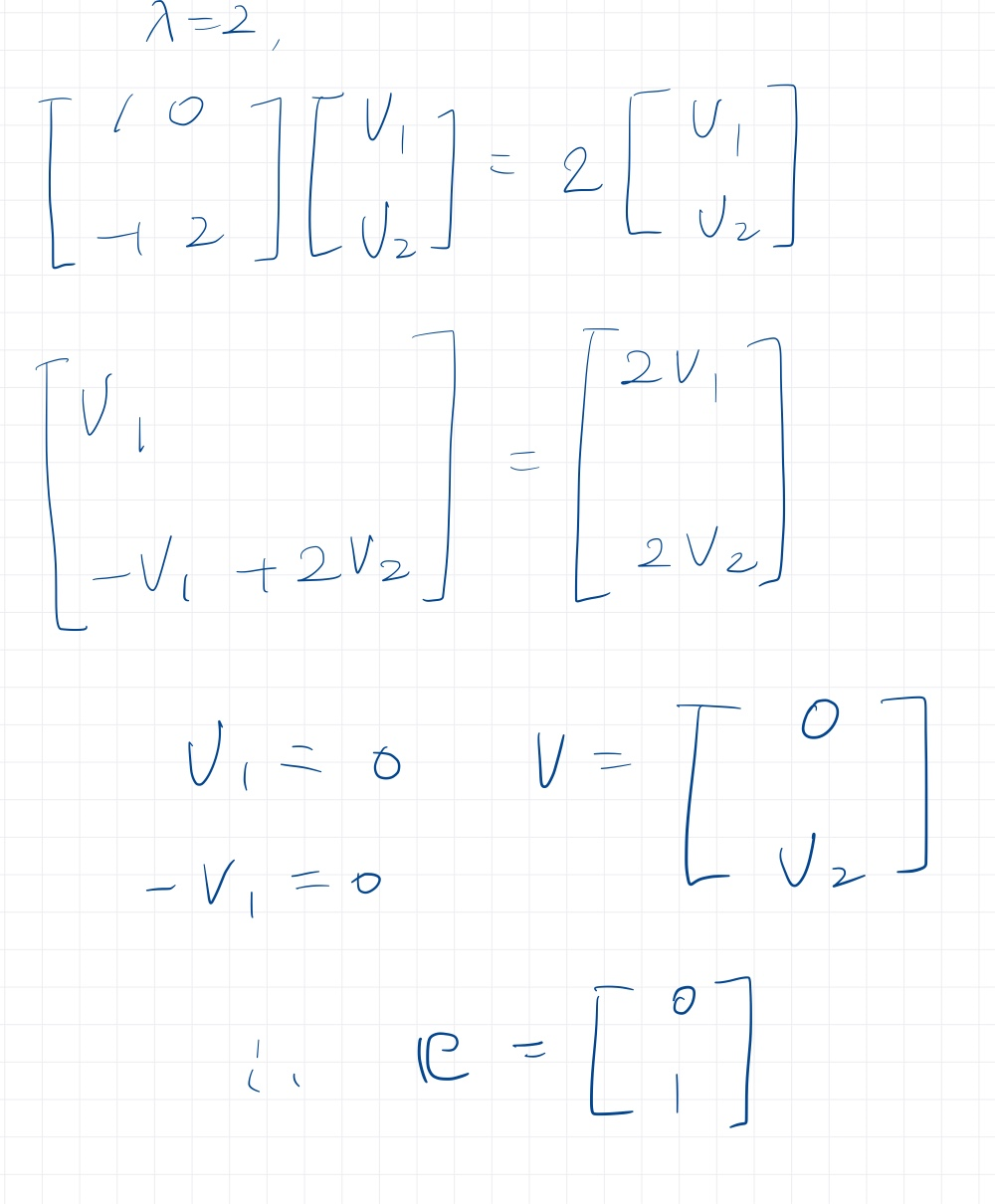
이러한 과정으로 고유값과 고유벡터를 구할 수 있다.

고유벡터는 상수를 곱하면 다같은 고유벡터이기때문에 크기가 1인 벡터로 정규화한다.
참고

이를 이용해 행렬 A를 표현할 수 있다.

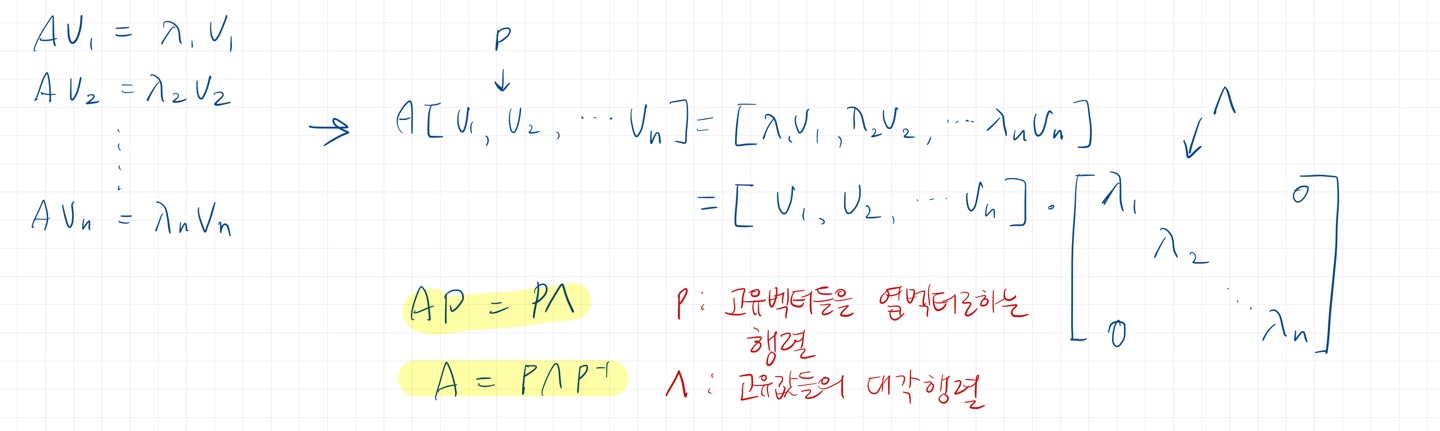
A = PΛP^-1 로 분해될 수 있다.

출처

• 행렬의 대각화 = 분해
• 모든 정방행렬이 고유값분해가 가능하진 않고, 고유벡터끼리 선형 독립이어야한다.
• 정방행렬이 서로 다른 고유값을 가진다면 고유벡터들은 선형 독립이다.
  -> 정방행렬 A가 서로 다른 고유값을 가진다면 고유값 분해 가능!

Spectrum decomposition

고유값분해의 특수한 경우라고 생각하면 된다.
행렬 A가 정방행렬,대칭행렬이라면

• 항상 고유값 분해가 가능
• 고유벡터들끼리 직교한다.
  PCA에서 공분산 행렬을 사용하므로, 이와같은 경우를 만족하게 된다.

이외 SVD(특이값분해)는 정방행렬이 아닌 행렬도 분해가능합니다.

PCA에서 고유값분해가 어떻게 쓰이는 지 알아보자

PCA

• 변수들의 전체분산 대부분을 소수의 주성분으로 설명하는 것이다.
• 고차원 데이터의 최대분산 방향을 찾아 새로운 저차원 공간에 투영한다.

1. 데이터의 공분산 행렬을 구한다.
   공분산행렬은 xx^T로, 데이터의 구조를 설명해준다고 한다.

2. 공분산 행렬의 스펙트럼 분해

3. 고유값이 큰 고유벡터로 정사영하여 차원 축소

코드로 표현하면 아래와 같다.

from sklearn.preprocessing import StandardScaler
import numpy.linalg as lin


def new_coordinates(X,eigenvectors,index):
    new = None
    for i in range(eigenvectors.shape[1]):
        if (i in index) and (new is None):
            new = [X.dot(eigenvectors.T[i])]
        elif i in index:
            val = [X.dot(eigenvectors.T[i])]
            new = np.concatenate((new, val),axis=0)
        else:
            continue
    return new.T


def MYPCA(X,number):
    # 정규화
    scaler = StandardScaler()
    X_std =  scaler.fit_transform(X) #sclaing 후 데이터
    features = X_std.T
    
    # 공분산 행렬 구하기
    cov_matrix = np.cov(features)
    
    # 공분산 행렬의 고유 벡터, 고유값
    eigenvalues = lin.eig(cov_matrix)[0]
    eigenvectors = lin.eig(cov_matrix)[1]
    
    # 소팅 후, number만큼 eigenvalue 선택
    eigenvalues = list(eigenvalues)
    sort_eigenvalues = sorted(eigenvalues, reverse=True)
    index = []
    for i in range(number):
        index.append(eigenvalues.index(sort_eigenvalues[i])) # projection해야할 eigenvector들의 index값을 구합니다.
    
    # eigenvector로 projection
    new = new_coordinates(X_std, eigenvectors, index)
    
    return new #새로운 축으로 변환되어 나타난 데이터 return