제 3고지 [DL from Scratch]

고차 미분 과정 시각화하기

시작하기 전 | 시각화 third-party module: plot_dot_graph

# step25.py
import numpy as np

# For Jupyter Notebook env
if "__file__" in globals():
    import os, sys
    sys.path.append(os.path.join(os.path.dirname(__file__), '..'))
from dezero import Variable
from dezero.utils import plot_dot_graph

25단계 & 26단계 | Backpropagtion 시각화하기 / goldstein 함수

1. goldstein 함수 선언

# step25.py
def goldstein(x, y):
    z = (1 + (x + y + 1) ** 2 * (19 - 14*x + 3*x**2 - 14*y + 6*x*y + 3*y**2)) * \
        (30 + (2*x - 3*y)**2 * (18 - 32*x + 12*x**2 + 48*y - 36*x*y + 27*y**2))
    return z

2. main 함수: BackPropagation 과정 시각화 1

if __name__ == "__main__":
    x = Variable(np.array(1.0))
    y = Variable(np.array(1.0))
    z = goldstein(x, y)
    z.backward()

    x.name = 'x'
    y.name = 'y'
    z.name = 'z'
    plot_dot_graph(z, verbose=False, to_file='goldstein.png')

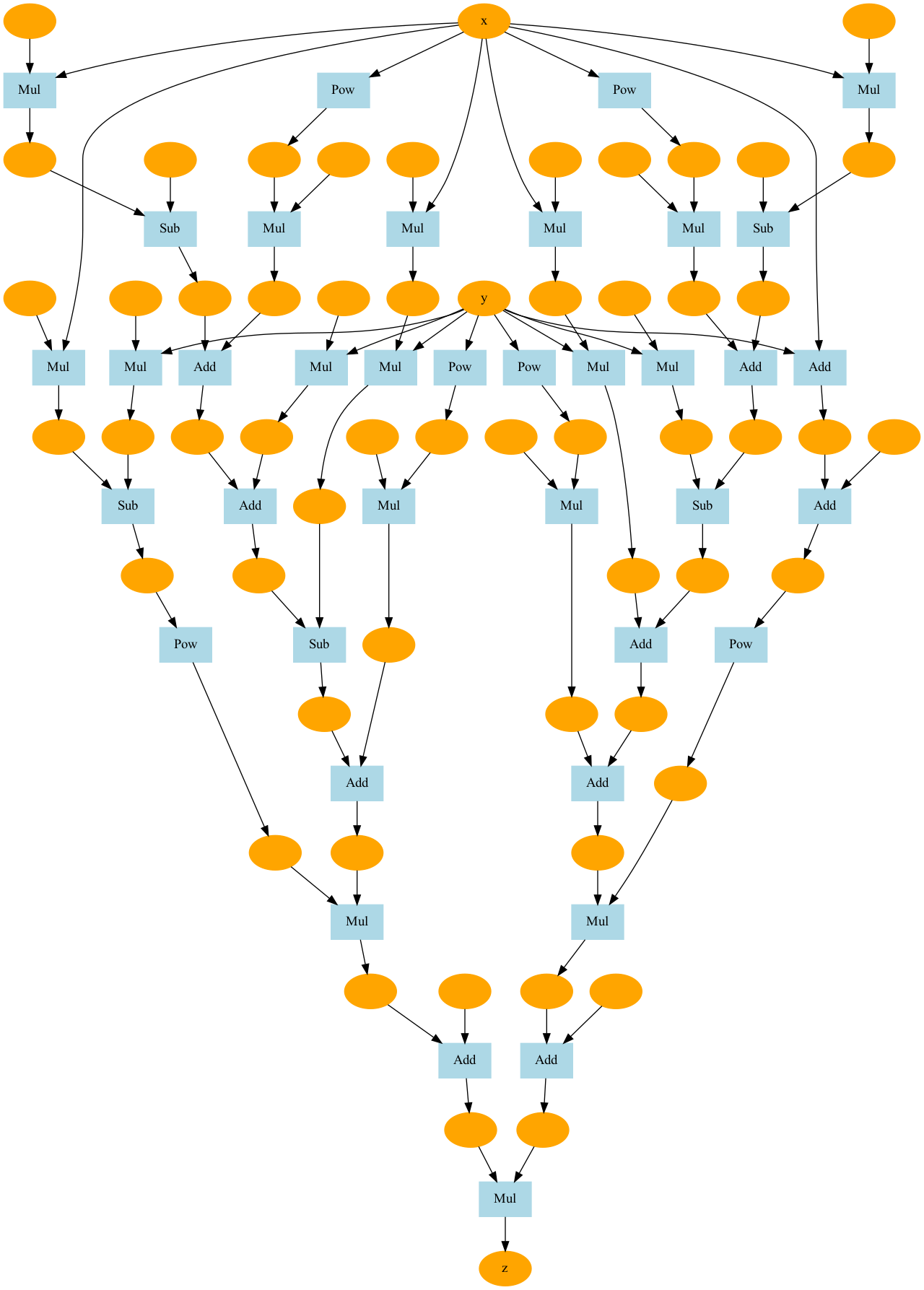
27단계 | Backpropagtion 시각화하기 / sin 함수

1. sin 함수 선언하기

class Sin(Function):
    def forward(self, x):
        y = np.sin(x)
        return y

    def backward(self, gy):
        x = self.inputs[0].data
        gx = gy * np.cos(x)
        return gx

def sin(x):
    return Sin()(x)

def my_sin(x, threshold=1e-150):
    y = 0
    for i in range(100000):
        c = (-1) ** i / math.factorial(2*i + 1)
        t = c * x ** (2 * i + 1)
        y = y + t
        if abs(t.data) < threshold:
            break

    return y

2. main 함수: BackPropagation 과정 시각화 2

• sin.png 출력하기

if __name__ == "__main__":
    x = Variable(np.array(np.pi/4))
    y = my_sin(x)
    y.backward()

    print(y.data)
    print(x.grad)

    x.name = 'x'
    y.name = 'y'

    plot_dot_graph(y, verbose=False, to_file='sin.png')

28 - 32단계 |

1. resenbrock 함수 선언하기

def rosenbrock(x0, x1):
    y = 100 * (x1 - x0 ** 2) ** 2 + (1 - x0) ** 2
    return y

2.

if __name__ == "__main__":
    x0 = Variable(np.array(0.0))
    x1 = Variable(np.array(2.0))
    lr = 0.001 # learning-ratio
    iters = 50000 # iterations

    for i in range(iters):
        print(x0, x1)

        y = rosenbrock(x0, x1)

        x0.cleargrad()
        x1.cleargrad()
        y.backward()

        x0.data -= lr * x0.grad
        x1.data -= lr * x1.grad

    # print(x0.grad, x1.grad)