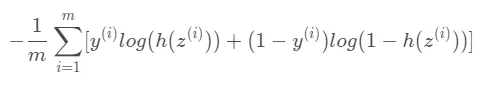논리 회귀

논리 회귀(Logistic Regression)

필요성

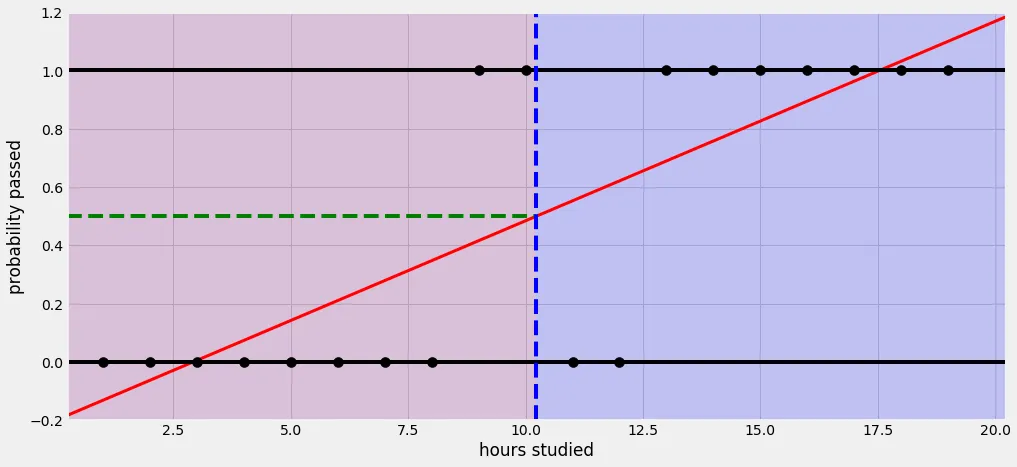
• 0과 1로 주어진 데이터를 이진 논리 회귀로 해결을 할 경우,

• 선형회귀를 사용할 경우, 위와 같은 그래프가 나오게되는데,

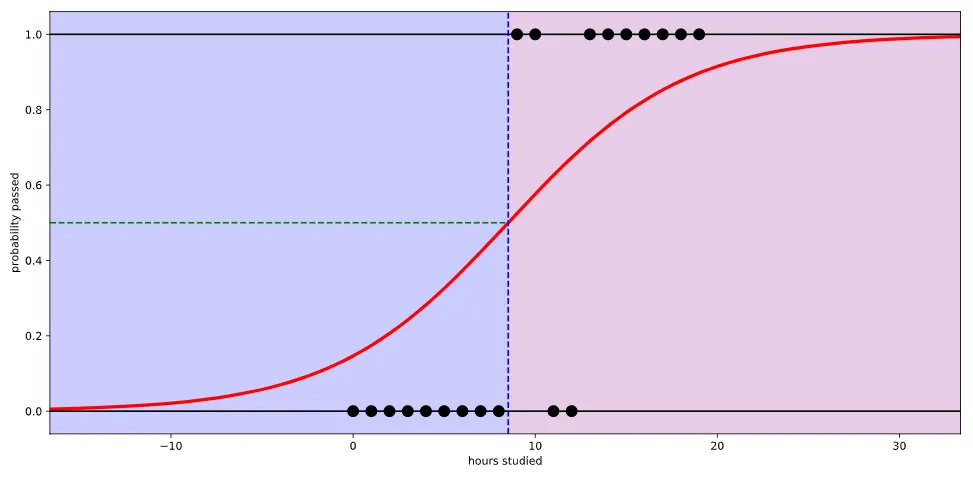
• 선형으로 풀수 없는 문제를 해결하는 다른 방법으로 나온것이 Logisitc Function(=Sigmoid function) 이다.

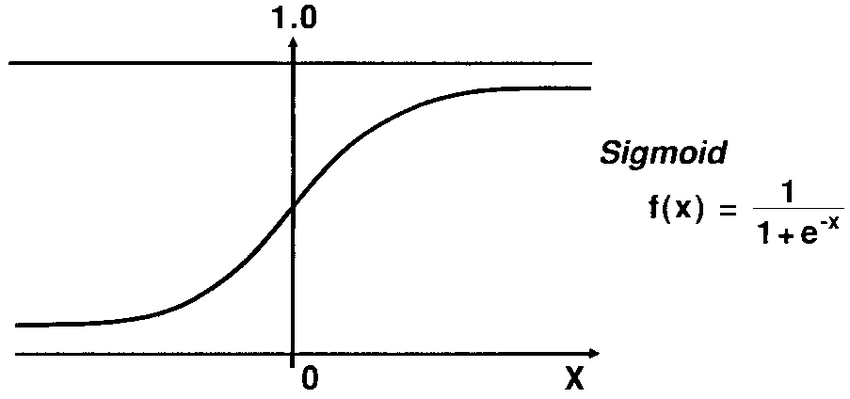
실제 많은 자연, 사회현상에서는 특정 변수에 대한 확률값이
선형이 아닌 S 커브 형태를 따르는 경우가 많다. 
이러한 S-커브를 함수로 표현해낸 것이 
바로 로지스틱 함수(Logistic function)이다. 
딥러닝에서는 시그모이드 함수(Sigmoid function)라고 불린다.

가설과 손실함수

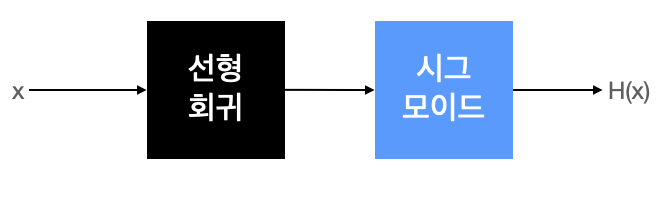
실질적인 계산은 선형 회귀와 동일하나, 출력에 시그모이드 함수를 붙여 0에서 1사이의 값을 가지도록 한다.

x가 음수로 갈수록 y가 0에 가까워지고,
x가 양수로 갈수록 y가 1에 가까워진다.

즉, 시그모이드 함수를 통과하면 0 에서 1사이의 값이 나온다.

[가설]

시그모이드 함수에 선형회귀식을 넣은 형태.

$H(x) = \frac{1}{1 + e^{-(Wx + b)}}$

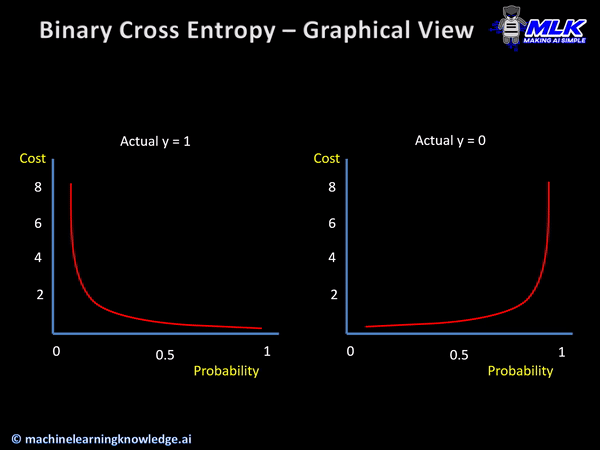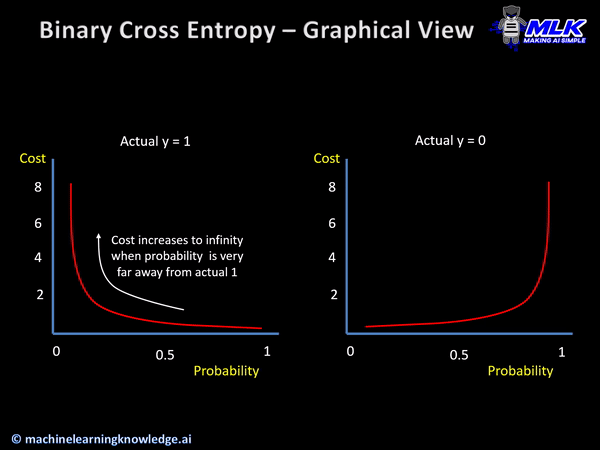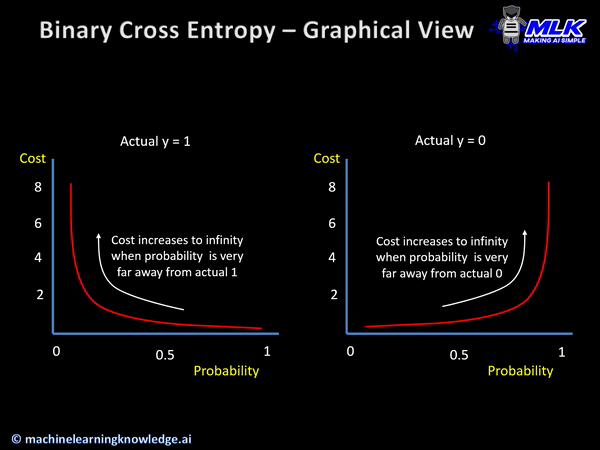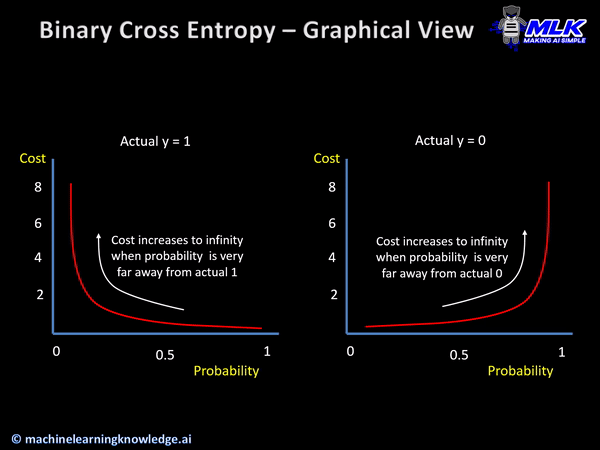
[손실 함수]

손실함수의 그래프는 다음과 같다.

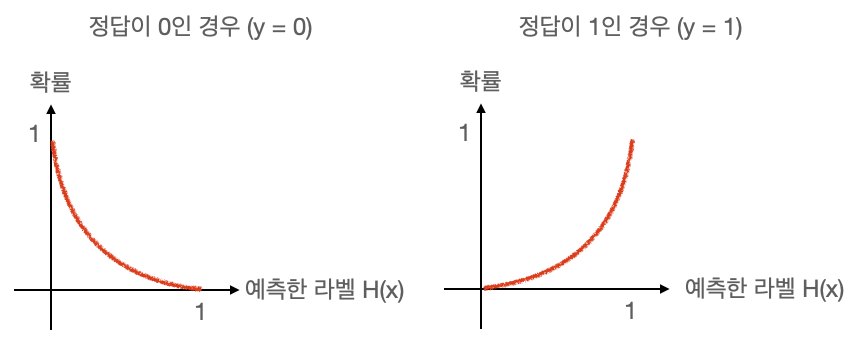
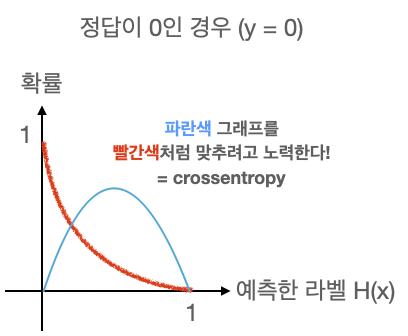
이에 따른 확률분포 그래프는 다음과 같다.

확률 분포 그래프를 비교할 때는 costentorpy 함수를 사용한다.

costentoryp 함수

• 임의의 입력값에 대해 원하는 확률 분포 그래프를 만들도록
  학습시키는 손실 함수.

입력값의 확률 분포가 파란색 그래프처럼 나왔을 경우,
파란색 그래프를 빨간색 그래프처럼 만들어주기 위해 노력하는 함수.

Keras에서 이진 논리 회귀의 경우 binary_crossentropy 함수를 사용한다.