[백준 C++] 11403. 경로 찾기

문제링크

문제

가중치 없는 방향 그래프 G가 주어졌을 때, 모든 정점 (i, j)에 대해서, i에서 j로 가는 경로가 있는지 없는지 구하는 프로그램을 작성하시오.

입력

첫째 줄에 정점의 개수 N (1 ≤ N ≤ 100)이 주어진다. 둘째 줄부터 N개 줄에는 그래프의 인접 행렬이 주어진다. i번째 줄의 j번째 숫자가 1인 경우에는 i에서 j로 가는 간선이 존재한다는 뜻이고, 0인 경우는 없다는 뜻이다. i번째 줄의 i번째 숫자는 항상 0이다.

출력

총 N개의 줄에 걸쳐서 문제의 정답을 인접행렬 형식으로 출력한다. 정점 i에서 j로 가는 경로가 있으면 i번째 줄의 j번째 숫자를 1로, 없으면 0으로 출력해야 한다.

예제 입력 / 출력

// 예제 입력 1
3
0 1 0
0 0 1
1 0 0

// 예제 출력 1
1 1 1
1 1 1
1 1 1

// 예제 입력 2
7
0 0 0 1 0 0 0
0 0 0 0 0 0 1
0 0 0 0 0 0 0
0 0 0 0 1 1 0
1 0 0 0 0 0 0
0 0 0 0 0 0 1
0 0 1 0 0 0 0

// 예제 출력 2
1 0 1 1 1 1 1
0 0 1 0 0 0 1
0 0 0 0 0 0 0
1 0 1 1 1 1 1
1 0 1 1 1 1 1
0 0 1 0 0 0 1
0 0 1 0 0 0 0

풀이

📍 플로이드 와샬 알고리즘

• 변의 가중치가 음이거나 양인 가중 그래프에서 최단 경로를 찾는 알고리즘
• 두 꼭짓점 간의 추정 최단 경로를 최적이 될 때까지 점진적으로 개선시켜 최단 경로를 찾음

📍 알고리즘

• 플로이드 와샬 알고리즘을 약간 변형시켜 두 정점간의 직접적인 연결이 없는 경우를 아주 큰 값 INF로 놓고 있는 경우는 1로 설정해 이어지는 경우를 1로 업데이트 해준다.

Ex.

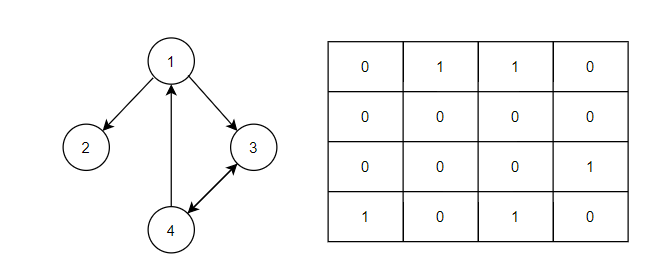
• 직접적인 경로가 존재하지 않는 구간을 INF로 바꿔준다.

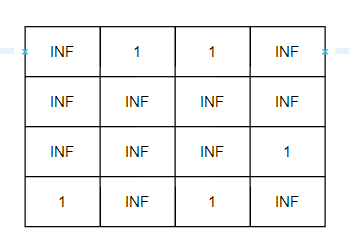
• 1 -> 1으로 가는 경로 사이에 임의의 구간 K을 집어넣어 그 경로가 존재한다면 1로 업데이트 시켜준다.

k = 1

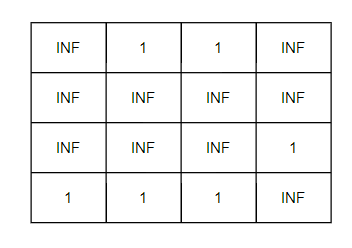
k = 2

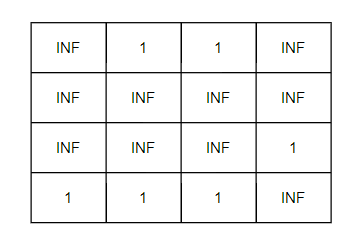
k = 3

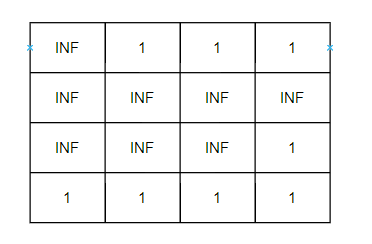
k = 4

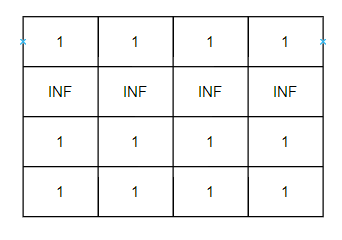
result

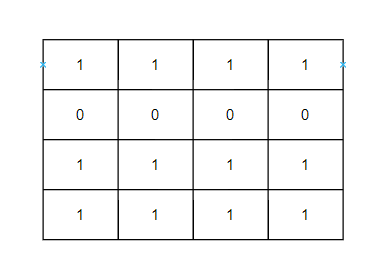
#include <iostream>
#include <unordered_set>

using namespace std;

int main(void) {

	int map[101][101];
	int N;
	const int INF = 1000;
	
	cin >> N;

	for (int i = 0; i < N; i++) {
		for (int j = 0; j < N; j++) {
			cin >> map[i][j];
			if (map[i][j] == 0) map[i][j] = INF;
		}
	}
  
	for (int k = 0; k < N; k++) {
		for (int i = 0; i < N; i++) {
			for (int j = 0; j < N; j++) {
				if (map[i][j] > map[i][k] + map[k][j]) 
					map[i][j] = 1;
			}
		}
	}

	for (int i = 0; i < N; i++) {
		for (int j = 0; j < N; j++) {
			if (map[i][j] == INF) cout << 0 << " ";
			else cout << 1 << " ";
		}
		cout << "\n";
	}


}